在化学和物理学里,核子(nucleon)是组成原子核的粒子,即质子或中子。每个原子核都拥有至少一个核子,每个原子又是由原子核与围绕原子核的一个或多个电子所组成。任意原子核种的质量数就是其核子数。因此有时人们也会称这个数字为“核子数”。

在1960年代之前,核子被认为是基本粒子,不是由更小的部份组成的。今天我们知道核子是复合粒子,由三个夸克经强相互作用捆绑在一起组成。两个或多个核子之间的交互作用称为核力,最终这也是强交互作用引起的。(在发现夸克之前,“强交互作用”一词只用于核子间的交互作用。)
核子研究属于粒子物理学和原子核物理学的交叉领域。粒子物理学,特别是量子色动力学,提供了解释夸克及强交互作用属性的公式。这些公式用定量方法解释夸克是如何结合成为中子和质子(以及所有其他的强子)。然而,当多个核子组合为一个原子核(核素)时,这些基础方程式变得非常难直接求解,必须使用核物理学的方法。核物理学利用近似法和模型来研究多个核子之间的交互作用,例如用核壳层模型。这些模型能够准确解释核素的属性,比如哪些核素会进行核衰变等。
质子和中子都是重子和费米子。质子和中子特别相似,除了中子不带有电荷以外,中子的质量比质子仅仅高0.1%,它们的质量非常相近,因此它们可以视为同样核子的两种状态,共同组成了一个同位旋二重态(I = 1⁄2),在抽象的同位旋空间做旋转变换,就可以从中子变换为质子,或从质子变换为中子。这两个几乎相同的核子都感受到相等的强相互作用,这意味著强相互作用对于同位旋空间旋转变换具有不变性。按照诺特定理,对于强相互作用,同位旋守恒。[1]:129-130
概述
质子和中子是原子核的组成部份,也能够在不组成原子的情况下单独存在。独立存在的质子就是氢-1(1H)的原子核。单独的中子是不稳定的(见下),但可以在核反应中出现,并在科学分析范畴派上用场。
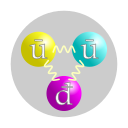
质子和中子均由三个夸克组成。质子由2个上夸克和1个下夸克组成,而中子则由1个上夸克和2个下夸克组成。强相互作用将这些夸克捆绑在一起。另一说法是,夸克是受胶子捆绑的,但实际上两种说法是等同的(胶子传递强相互作用)。
每个上夸克的电荷为+2⁄3 e,而每个下夸克的电荷为−1⁄3 e,所以质子和中子的总电荷分别为+e和0。“中子”一词便源自其电“中性”的属性。
质子和中子的质量相当:质子的为1.6726×10−27 kg或938.27 MeV/c2,而中子的则为1.6749×10−27 kg或939.57 MeV/c2。中子相对较重大约0.1%。两者质量的相近能够通过粒子物理学中的上夸克和下夸克的质量差来解释。[1]:135-136
质子和中子的自旋为1⁄2。这意味著它们是费米子而非玻色子,因此与电子一样,它们也遵守包利不相容原理。这在核物理学中是非常:一个原子核中的中子和质子不能同时占据相同的量子态,而是会分散开来形成核壳层,这和在化学里电子形成电子壳层的原理相似。质子和中子自旋的重要性也在于,它是大原子核的核自旋的来源。核自旋的其一重要应用在于化学和生化分析中的核磁共振成像。
质子的磁矩,写作μp,是2.79 核磁子(μN),而中子的磁矩则为μn = −1.91 μN。这些参数在核磁共振成像中也是十分重要的。
单独存在的中子是不稳定的:它会进行β衰变(一种放射性衰变),变为质子、电子和一个反电中微子,半衰期约为10分钟(见中子)。质子单独存在时是基本稳定的,或者其衰变率过于慢,无法探测得出。(这是粒子物理学中重要的课题,见质子衰变。)
在一个原子核里,依不同的核素而定,质子和中子可以是稳定或不稳定的。在某些核素里,中子能够转变为质子(加上其他粒子);在另一些核素里,反过程亦可发生,质子会通过β+衰变或电子捕获变为中子(加上其他粒子);又在其它核素中的质子和中子均为稳定的,不会进行转变。
两种核子都有其对应的反粒子:反质子和反中子。这些反物质粒子的质量和其正粒子的相同,但电荷正负相反,它们的相互作用与正粒子之间的无异。(一般而言,物理学者相信这结果“完全”正确,原因是CPT对称。如果确实存在差异,则差异必定太小,以致实验至今仍未能探测得出。)而且,反核子能够结合形成“反原子核”。到目前为止,科学家已经制成反氘[2][3]以及反氚[4]原子核。
详细属性表
| 粒子名 | 符号 | 含夸克 | 不变质量(MeV/c2) | 不变质量(u) | I3 | JP | Q(e) | 磁矩 | 平均寿命(s) | 一般衰变为 |
|---|---|---|---|---|---|---|---|---|---|---|
| 质子[PDG 1] | p / p+ / N+ |
u u d |
938.272013±0.000023 | 1.00727646677±0.00000000010 | +1⁄2 | 1⁄2+ | +1 | 2.792847356±0.000000023 | 稳定 | 尚未观察到 |
| 中子[PDG 2] | n / n0 / N0 |
u d d |
939.565346±0.000023 | 1.00866491597±0.00000000043 | -1⁄2 | 1⁄2+ | 0 | −1.91304273±0.00000045 | (8.857±0.008)×10+2 | p + e− + ν e |
| 反质子 | p / p− / N− |
u u d |
938.272013±0.000023 | 1.00727646677±0.00000000010 | -1⁄2 | 1⁄2+ | −1 | −2.793±0.006 | 稳定 | 尚未观察到 |
| 反中子 | n / n0 / N0 |
u d d |
939.485±0.051 | 1.00866491597±0.00000000043 | +1⁄2 | 1⁄2+ | 0 | ? | (8.857±0.008)×10+2 | p + e+ + ν e |
^a 质子和中子质量的准确度在用原子质量单位(u) 时比用MeV/c2时准确得多,因为基本电荷的准确度相对较低。此处用的对换关系为1 u = 931.494028±0.000023 MeV/c2。 正反粒子的质量是假设相同的,至今没有实验能够驳斥这一点。目前的实验显示,如果正反质子之间有质量上的差异的话,其出入小于2×10−9 MeV/c2,[PDG 1]而正反中子的质量差异则小于(9±6)×10−5 MeV/c2。[PDG 2]
^c 假设为自由中子;多数原子核中的中子都是稳定的。
核子共振态指的是核子的激发态,一般对应于核子中某个夸克拥有反转了的自旋态,或对应于该粒子衰变时的轨道角动量。下表只列出粒子数据组(PDG)评级为3或4星的共振态。由于半衰期极短,以下许多粒子的属性仍在研究当中。
符号的格式为N(M) L2I2J,其中M为粒子质量的近似值,L为核子-介子对衰变时产生的轨道角动量,而I和J分别为粒子的同位旋及总角动量。由于核子的同位旋被定义为1⁄2,因此第一个数字必然为1,而第二个数字则永远是奇数。在谈到核子共振态的时候,有时会省略N,而且表达式顺序会颠倒:L2I2J (M)。例如,质子的符号可以写成"N(939) S11"或者"S11 (939)"。
下表只列出基共振态,每一栏代表4个重子:2个核子共振粒子,和2个它们的反粒子。每个共振态的存在形态可以是带正电荷(Q)的,并含夸克
u
u
d
,就像质子一样;或者是电中性的,含夸克
u
d
d
,就像中子一样;又或者是两种反粒子,分别含反夸克
u
u
d
和
u
d
d
。由于不含有奇夸克、粲夸克、底夸克和顶夸克,这些粒子不具备奇异数、魅数、底数及顶数。下表只列出同位旋为1⁄2的共振态,具3⁄2同位旋的共振态请参看Δ粒子条目。
| 符号 | JP | 质量平均数 (MeV/c2) |
总宽度 (MeV/c2) |
极位置 (实数部分) |
极位置 (−2 × 虚数部分) |
通常衰变为 (Γi /Γ > 50%) |
|---|---|---|---|---|---|---|
| N(939) P11 [PDG 3]† |
1⁄2+ | 939 | † | † | † | † |
| N(1440) P11 [PDG 4] 亦称罗佩尔共振态 |
1⁄2+ | 1440 (1420–1470) |
300 (200–450) |
1365 (1350–1380) |
190 (160–220) |
N + |
| N(1520) D13 [PDG 5] |
3⁄2- | 1520 (1515–1525) |
115 (100–125) |
1510 (1505–1515) |
110 (105–120) |
N + |
| N(1535) S11 [PDG 6] |
1⁄2- | 1535 (1525–1545) |
150 (125–175) |
1510 1490 — 1530) |
170 (90–250) |
N |
| N(1650) S11 [PDG 7] |
1⁄2- | 1650 (1645–1670) |
165 (145–185) |
1665 (1640–1670) |
165 (150–180) |
N + |
| N(1675) D15 [PDG 8] |
5⁄2- | 1675 (1670–1680) |
150 (135–165) |
1660 (1655–1665) |
135 (125–150) |
N |
| N(1680) F15 [PDG 9] |
5⁄2+ | 1685 (1680–1690) |
130 (120–140) |
1675 (1665–1680) |
120 (110–135) |
N + |
| N(1700) D13 [PDG 10] |
3⁄2- | 1700 (1650–1750) |
100 (50–150) |
1680 (1630–1730) |
100 (50–150) |
N |
| N(1710) P11 [PDG 11] |
1⁄2+ | 1710 (1680–1740) |
100 (50–250) |
1720 (1670–1770) |
230 (80–380) |
N |
| N(1720) P13 [PDG 12] |
3⁄2+ | 1720 (1700–1750) |
200 (150–300) |
1675 (1660–1690) |
115–275 | N |
| N(2190) G17 [PDG 13] |
7⁄2- | 2190 (2100–2200) |
500 (300–700) |
2075 (2050–2100) |
450 (400–520) |
N + |
| N(2220) H19 [PDG 14] |
9⁄2+ | 2250 (2200–2300) |
400 (350–500) |
2170 (2130–2200) |
480 (400–560) |
N + |
| N(2250) G19 [PDG 15] |
9⁄2- | 2250 (2200–2350) |
500 (230–800) |
2200 (2150–2250) |
450 (350–550) |
N + |
† P11(939)核子是普通质子或中子的激发态,如位于原子核里的核子。这些粒子在原子核里基本稳定,如锂-6。
夸克模型分类
在具有SU(2)味的夸克模型里,两种核子是基态二重态的成员。质子的夸克组合为uud,而中子的夸克组合则为udd。在具有SU(3)味的模型中,它们是自旋为1⁄2重子形成的基态八重态的成员,称为八重道。除了中子与质子以外,此八重态的其它成员都是超子。这包括奇异同位旋三重态
Σ+
,
Σ0
,
Σ−
、
Λ
以及奇异同位旋二重态
Ξ0
,
Ξ−
。在具有SU(4)味(添入粲夸克)的模型中,这多重态还可以延伸至基态20重态。在具有SU(6)味(添入顶夸克和底夸克)的模型中,可以延伸至基态56重态。
参见
延伸阅读
- A.W. Thomas and W.Weise, The Structure of the Nucleon, (2001) Wiley-WCH, Berlin, ISBN 3-527-40297-7/ ISBN 978-3-527-40297-7
- Brown, G. E.; Jackson, A. D. The Nucleon–Nucleon Interaction. North-Holland Publishing. 1976. ISBN 0-7204-0335-9.
- Vepstas, L.; Jackson, A.D.; Goldhaber, A.S. Two-phase models of baryons and the chiral Casimir effect. Physics Letters B. 1984, 140 (5–6): 280–284. Bibcode:1984PhLB..140..280V. doi:10.1016/0370-2693(84)90753-6.
- Vepstas, L.; Jackson, A. D. Justifying the chiral bag. Physics Reports. 1990, 187 (3): 109–143. Bibcode:1990PhR...187..109V. doi:10.1016/0370-1573(90)90056-8.
- Nakamura, N.; et al. (Particle Data Group). Review of Particle Physics. Journal of Physics G. 2011, 37 (7): 075021. Bibcode:2010JPhG...37g5021N. doi:10.1088/0954-3899/37/7A/075021.
参考资料
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.



 ,
,  ...
...


