Loading AI tools
用于描述地球形状的物理表面 来自维基百科,自由的百科全书
大地水准面(德语:Geoid)是指地球重力场[注 1]中,与处于自由静止状态的平均海水面相重合[3]:49或最为接近[4]:42的重力等位面。这一概念最早由德国大地测量学家卡尔·弗里德里希·高斯在1828年提出。当时,高斯以“地球的数学表面”[3]:73来指称与重力方向相垂直、且与静止的平均海水面相重合的几何表面[5]:4,并提出将其作为高程系统的基准面[6]:74。其后,高斯的学生利斯廷于1873年创造出了“Geoid”一词,用以描述高斯所提出的数学表面。[7]

在大地测量学中,大地水准面被视作是地球的物理形状和数学形状。[4]:2由于自然的地形表面形态过于复杂,大地测量学通常是将重力场中整体形状与地形表面最为接近的等位面作为地球的形状进行研究。[8]:226处于静力平衡状态下的平均海水面被视作是符合这一标准的重力等位面,这一假想的海水面不受潮汐、风浪及大气压的变化影响,仅在地球引力和因地球自转产生的离心惯性力的作用下保持平衡。[9][4]:41将该平均海水面所处的重力等位面延伸到陆地内部,形成的闭合曲面即为大地水准面,其所包围的形体又被称为大地体。[10]:29
1849年,英国物理学家斯托克斯提出了计算大地水准面的斯托克斯方法,使大地水准面的形状能够通过其整个表面上的重力观测值确定。[10]:8但在传统的大地测量中,通过大范围的重力观测,以及对这些重力观测值进行积分而求得大地水准面的方式遇到了诸多困难。[8]:294-295随着20世纪中后期卫星重力测量等技术逐渐发展成熟,采用球谐级数表达的地球重力场模型逐渐成为了描述大地水准面的主要方式[11],全球尺度下的大地水准面也得以以分米级的精度测定[12]。莫洛坚斯基、布耶哈马等大地测量学家,亦在斯托克斯方法的基础上提出了通过地面测量技术确定大地水准面的新方法。[5]:34
大地水准面是测量外业所依据的基准面,在测量学中具有重要地位。[13]在各类高程系统中,日常中称为海拔高程的正高系统是基于大地水准面建立的。[10]:42如何确定大地水准面的形状,是物理大地测量学研究的关键问题之一。[14][15][16]
1873年,利斯廷提出了大地水准面的经典定义,即大地水准面是与平均海水面相重合的重力等位面。[7]在1975年,美国大地测量学家理查德·拉普(英语:Richard H. Rapp)进一步完善了这一定义,他将重力位 视为除大气层外的地球质量所引起的重力位 、大气质量所引起的重力位 ,以及受日、月的引潮力作用而引起的重力位 的和:[17]
不同于 ,后两项与地球内部的质量分布无关,因此可以被相对精确地计算。拉普认为,定义大地水准面的重力位应当仅包含 和 ,即大地水准面应当是使 等于常数的重力等位面,而因引潮力、风和洋流等其他因素影响产生的变化则不在考虑范围之内。这种定义方式认为,通过多年的验潮数据可以得到一个平均海水面,其上的任意一点的位置与海洋面的长期平均位置相重合。[18]
然而,20世纪60年代以来对平均海水面的研究发现,其与大地水准面间存在最大可达2米的系统性的偏移[19],这就使大地水准面的经典定义暴露出了缺陷。因此,马瑟(英语:Mather R. S.)等人在1978年提出,大地水准面应重新定义为与平均海水面最为密合的重力等位面。[20]
1985年,瑞典大地测量学家布耶哈马基于相对论重力提出了相对论大地水准面的概念,即一个使其上所有精密时钟的运行速率相同且与平均海水面最为密合的封闭曲面。[21]在2019年,德国不来梅大学的丹尼斯·菲利普(德语:Dennis Philipp)利用新的测量结果,以及无含时红移势能(英语:time-independent redshift potential)等新的理论,对相对论大地水准面的概念给出了数学上的表述方法。这一方法给出的相对论水准面与经典大地水准面之间存在着毫米级的差异。[22]

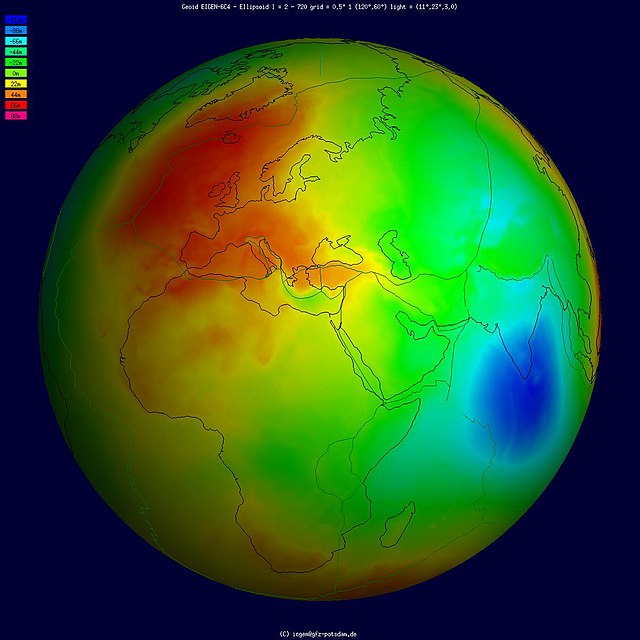
从数学上看,大地水准面是一个连续但不规则的闭合曲面,它与经过这一曲面的铅垂线处处正交。[23]:49地球内部的质量分布,特别是外层的质量分布的不均匀性,使得大地水准面的形状变得特别复杂。[10]:29在发生密度突变的区域,大地水准面的曲率会表现出不连续性。因此,大地水准面并非是解析曲面。[4]:41
大地水准面的形状可以用椭球面近似,该椭球面也被称为参考椭球面。以WGS84坐标系使用的椭球为例,其长半轴位于赤道面上,长度约6,378,137米;短半轴指向极点,长度约6,356,752米,比长半轴短约21千米。[24]相对于WGS84椭球,大地水准面的起伏从最高点到最低点的范围仅不到200米。在这一差距被放大的情况下,大地水准面的形状则与土豆或梨相似。[25]尽管大地水准面是一个不规则的曲面,但它仍比真实的地形表面更加平滑,后者的高程差跨越了近20千米。
 |
 |
大地水准面起伏又称大地水准面高或大地水准面差距,是指大地水准面上的某一点,与其沿法线投影到参考椭球面上的相应位置之间的距离。[23]:83大地水准面高的正极值出现在新几内亚,为+85.4米;负极值出现在印度南部,为−107.0米。[26]
大地水准面起伏的幅度和空间分布受地球内部密度分布的直接影响。在频谱分析中,大地水准面起伏的分布可分为长波(尺度为上千公里,幅度为±100米左右)、中波(尺度为上百公里,幅度为±10米)和短波(尺度为数十公里,幅度为±1米)部分。[26]其中,长波部分反映地幔及地球内部的密度异常分布[27],而中短波部分则反映岩石圈和地形的影响。在地球物理学研究中,大地水准面的起伏又可分为地形的不规则部分、结晶基底起伏、莫霍面起伏、岩石圈底面起伏,以及因地幔和地核部分的横向密度不均匀造成的起伏等。[28]

大地水准面高在北大西洋、欧洲、非洲的西部和南部、印度洋西南部、安地斯山脉、西太平洋及赤道太平洋部分等地表现出正值[29][30],世界上所有的大型地盾、显生宙地台和地质热点几乎也都位于这些地区[31]。其中,分布较广而幅度较高的有两个区域,横跨了大西洋和非洲的正异常区域被称为大西洋-非洲大地水准面高值区(英语:Atlantic-African geoid high),太平洋中西部的正异常区域则被称为赤道太平洋大地水准面高值区(英语:Equatorial Pacific geoid high)。西太平洋的正异常区域在中生代早期曾是俯冲杂岩带所处的位置。其他与俯冲带不相关的正异常区域则可能曾是大陆板块的聚集处,或是古板块的中心等会发生地幔绝热现象的地区。地幔的绝热会使得其本身的温度升高,其产生的抬升和岩浆作用能够产生大地水准面的正异常。[31]
大地水准面高在印度及印度洋北部,以及南极洲附近表现出负值。其中又以印度洋北部的区域表现得尤其显著,该区域也被称为印度洋大地水准面低值区(英语:Indian Ocean geoid low)。[32]对于这些负异常形成的原因,存在有众多推测,如软流层中的浅层物质流[32]、板块俯冲在中地幔引起的地幔对流[33],以及地幔和地核的边界处发生的凹陷[34]等。同时,这些推测也都同意,印度洋大地水准面低值区出现的部分原因是特提斯洋在中生代的俯冲带来的密度异常。[35]

测定大地水准面进行的技术手段有多种,包括在地面、船舶和飞机中直接进行重力测量,或是通过天文方法和卫星导航系统进行水准测量以获取垂线偏差或大地水准面高,又或是利用雷达和人造卫星进行卫星测高来描绘地形表面的高度,以及通过对卫星轨道摄动情况的分析、卫星跟踪卫星以及卫星重力梯度测量等卫星重力探测技术直接反演地球重力场的中长波分量等。[36][37][38][6]:318-319其所依据的原理是对地面的重力测量数据进行积分(如斯托克斯方法),或将地球重力场以球谐级数的形式表达(如拉普拉斯方法)。[39]
在人造卫星出现前,斯托克斯方法是测定大地水准面的主要原理,但这种方式在应用过程中存在诸多困难:斯托克斯公式中的积分难以收敛、全球性的观测数据难以获得等。[11]1957年斯普特尼克卫星的升空,揭示了通过人造卫星反演地球重力场的可能性。[40]从此,使用拉普拉斯方法构建全球的重力场模型,成为了大尺度上表达大地水准面的主要方式。[11]21世纪后,诸如CHAMP、GOCE和GRACE等新一代重力测量卫星的出现,得以使对地球重力场的研究以空前的精度和空间分辨率进行,还使得对地球重力场的时变监测成为可能。[41][42]
乔治·斯托克斯在1849年提出的斯托克斯定理指出:[43]在大地水准面的外部没有质量分布的情况下,其形状和其外部的重力场可以由地球的质量、自转角速度以及大地水准面上的重力观测值唯一确定,而与其内部的质量分布无关。[23]:17这一定理说明,大地水准面的形状可以通过地面上的重力观测数据确定。而利用斯托克斯方法确定大地水准面的形状,需要确定大地水准面高相对于参考椭球面的高程差(即大地水准面高)以及这一高程差在参考椭球面上的位置。[8]:284这分别可以用斯托克斯公式和维宁·曼尼兹公式进行计算。
值得注意的是,实际上的重力观测数据是在地形表面,而非大地水准面上得到的。因此,在得到地表的观测数据后,还需要除去大地水准面外的质量对重力观测值的影响,并将地面上重力观测值的位置改正到大地水准面上,这一部分的内容又被称为重力归算。[8]:264通过斯托克斯方法,可以求得较高精度的高程异常并随之确定相应的大地水准面高,常用于局部重力场模型的建立。[23]:329
斯托克斯公式给出了大地水准面高与全球大地水准面上的重力异常及其分布的数学关系:[43]
上式中, 是大地水准面高, 是地球的平均半径[23]:87, 是全球正常重力的平均值。而对于积分部分,表示在整个单位球面上的积分, 是立体角元素。[23]:89 是单位角元素上的重力异常,由重力测量数据给出的重力位减去计算得到的正常重力位后得到。 则为斯托克斯函数[44],该项是单位球面上的被计算点与重力异常观测值所在的角元素之间的夹角 的函数。[23]:94
在由斯托克斯公式求得大地水准面相对于参考椭球面的高程差后,还需通过垂线偏差改正,将大地水准面上的天文坐标转换成参考椭球面上的地理坐标。这项改正能够通过通过维宁·曼尼兹公式计算:[23]:114
上式中的 表示天文坐标相对于地理坐标的纬度差, 表示天文坐标相对于地理坐标的经度差, 则是天文坐标相对于地理坐标的方位角。
利用引力位在质体外部满足拉普拉斯方程的特性[23]:5,可以将其展开成球谐级数进行逼近,球谐级数中的各项系数由地球的各项物理性质确定。这些物理性质,如地球的扁率和重力的不规则性等,会对人造卫星在空间中的运动造成影响,即卫星轨道的摄动。因此通过对卫星轨道进行动力学分析,可以反演出地球的重力场模型。[45]:149又由于人造卫星对重力场模型中的高阶项并不敏感[6]:319,人造卫星主要用于获得重力场模型中的低阶项,而高阶项还需结合地面的重力观测数据等其他方式获得。[16]
通过求解球面坐标中的拉普拉斯方程 ,单位球外部()的引力位可以展开为:[23]:59
上式中各个量的含义如下:
上式中的向径 是被计算点相对于单位球的相对半径,而非其相对于地心的真实距离。
上式中各个量的含义如下:
在这一表达式中,参数 、、和 均由地球本身的特性决定,包含了地球的转动惯量和动力学形状等信息,是引力场模型中的待解参数。[23]:61-63

大地水准面是通过重力场模型进行表达的,对全球的重力场进行描述的模型即为全球重力场模型。[46]在建立重力场模型的过程中,重力位 被分成引力位 和离心力位 两部分(即 ), 其中离心力位 能够根据地球的自转角速度 和点在空间中的坐标 直接计算得到:[23]:47
引力场位的确定比离心力位的确定要复杂得多,引力场模型的建立是重力场模型建立过程中的主要部分。因此,在不严谨的表述中,有时也将引力场模型直接称为重力场模型。[46]
在引力场模型中,引力位 在地球外部()表达为如下形式:[47]
上式中的各个量的含义如下:
其中,当 时,,,则求和符号右侧所有项的和为 ;当 时,,则求和符号右侧所有项的和为 . [47]因此,上式可进一步表达为如下形式:
在得到引力位 和椭球面坐标为 的关系后,再将其与离心力位模型 相加,即可得到重力位模型 ,最后得到表达为 的大地水准面的形状。[23]:48 在实际的模型建立的过程中,也常取引力位中的数阶最大项作为正常重力场中的引力位,再将余下的引力位以扰动位的形式进行表达,而正常重力场中的等位面即为参考椭球面。[8]:207-212
根据奈奎斯特采样定理,球谐函数表达式中的阶次越高,其表达的范围也就越精细。对于以球谐函数来表达的重力场模型,其空间分辨率通常以最短半波长表示。在地球表面,模型的空间分辨率 与最大阶数 的关系为:[46]
其中的 为地球的平均半径。通过这一公式,可以求出现有重力场模型常采用的空间分辨率:
| 最大阶数 | 最短半波长 / km |
|---|---|
| 100 | 200.00 |
| 200 | 100.00 |
| 360 | 55.55 |
| 2190 | 9.13 |
在美国国家地理空间情报局(NGA)发布的EGM96模型中,,即该模型给出了最高完全阶次至360的重力场模型系数,其表达的大地水准面的分辨率可达55千米或110千米(取决于对分辨率定义的不同)。而在2009年,NGA又发布了最大阶数 ,最高完全阶次为2159次的EGM08模型,其大地水准面的分辨率可达12千米,精度在全球范围内可达±15厘米。[48][12]
现有的地球重力场模型由国际地球重力场模型中心(ICGEM)负责收集和存档。[49]截至2020年,ICGEM存储的阶数超过2000阶的超高阶静态全球重力场模型有如下几个:
| 模型 | 发布时间 | 最高阶数 | 数据来源 | 参考文献 |
|---|---|---|---|---|
| EGM2008 | 2009年 | 2190 | A、G、S(Grace) | [48] |
| EIGEN-6C4 | 2014年 | 2190 | A、G、S(Goce、Grace、Lageos) | [50] |
| GECO | 2015年 | 2190 | EGM2008、S(Goce) | [51] |
| SGG-UGM-1 | 2018年 | 2159 | EGM2008、S(Goce) | [52] |
| XGM2019e_2159 | 2019年 | 760/2190/5540 | A、G、S(GOCO06s)、T | [53] |
| 注:其中A表示测高数据,S表示为卫星测量数据,G表示地表测量数据(包括陆地、船舶和航空测量),T表示测图数据 | ||||

大地水准面是正高系统的参考面,正高被定义为地面上任意一点沿其所在的铅垂线到大地水准面的距离。[23]:166在重力水准测量中,观测到大地水准面上一点 与任意一点 之间的重力位差,再求得点 沿铅垂线到大地水准面的路径上的重力平均值 ,可计算得点 的正高为:[10]:42
一个正高系统必须与一个重力位已知的大地水准面相联系,这个重力位即为大地水准面重力位。
在大地测量学以外的领域,正高也被称为海拔高度。[23]:172而在进行空间位置的计算(如计算GPS等全球卫星导航系统中的卫星位置)时,使用的高度则是相对于参考椭球面的距离,称为大地高或椭球高。两者间的转换需要通过大地水准面高进行:[54]
其中, 表示大地高(椭球高), 表示正高, 表示大地水准面高。
正高的计算需要用到重力平均值 ,但该值无法在地球内部的质量和重力分布未知的情况下得到,所以正高无法被精确求得。[8]:3511945年,苏联大地测量学家莫洛坚斯基提出了利用正常高来代替正高的计算方式。[55]在这一高程系统中,由地球表面向下量取正常高而获得的表面被称为似大地水准面,由正常椭球面向上量取正常高而获得的表面则被称为似地形表面,而似大地水准面和正常椭球面之间的差距又被称为高程异常。[56]似大地水准面与水准面不同,它没有具体的物理意义,更不是重力等位面,只是用于计算的辅助面。[23]:294大地水准面和似大地水准面在山区的差异可达4米,但两者在平均海水面上是重合的。[8]:352
大地水准面重力位 与高程基准相互对应,是人为规定的参考值。这一参考值应具有不随时间变化、长期固定,且与平均海水面的高度有明确关系的特征。[57]在2015年,国际大地测量协会(IAG)公布的大地水准面重力位参考值为。[58][59]但在不同的区域高程系统中,其定义的高程系统仍可能对应出不同的大地水准面重力位值。以中国1985国家高程基准为例,其与全球平均大地水准面的差异为21到23厘米。[60]
在加拿大、北欧和南极洲等地,冰后回弹效应会使得大地水准面发生每年多达2毫米的变化,垂直方向上的地壳构造运动亦会使大地水准面发生微小的变动。[61]:170-171在建立高精度的高程系统时候,考虑这些大地水准面的时变现象是非常有必要的。[62]:24重力测量卫星可以用于这类时变现象的监测。以GRACE卫星为例,其对长波时变重力场的时间分辨率可达10天,测定的大地水准面年变化率精度为0.01毫米每年。[63]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.