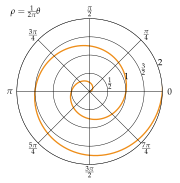
阿基米德螺线

阿基米德螺旋线（Archimedean spiral），亦称“等速螺线”。当一点P沿动射线OP以等速率运动的同时，这射线又以等角速度绕点O旋转，点P的轨迹称为“阿基米德螺线”。它的极坐标方程为：${\displaystyle \,r=a+b\theta }$。这种螺线的每条臂的间距永远相等于${\displaystyle 2\pi b}$。

• 
  阿基米德螺线360度
• 
  极坐标图

应用

涡卷式压缩机运转原理

准确地利用阿基米德螺线，可以三等分任意角。但是因为阿基米德螺线无法利用尺规作出，故几何三大难题中的三等份任意角仍然稳坐其宝座。

阿基米德螺线的画法

• 一、以适当长度（OA）为半径，画一圆O。
• 二、作一射线OA。
• 三、作一点P于射线OA上。
• 四、模拟点A沿圆O移动，点P沿射线OA移动。
• 五、画出点P的轨迹。
• 六、结果。（隐藏圆O、射线OA &点P）

参见

• 双曲螺线
• 圆内螺线
• 柯奴螺线
• 等角螺线
• 费马螺线
• 连锁螺线