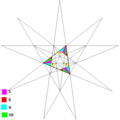
五复合立方体
来自维基百科,自由的百科全书
在几何学中,五复合立方体,是一种由五个立方体组合成的复合多面体,其索引编号为UC9,是唯一五种正复合体之一[3],亦是一种星形多面体。埃德蒙·赫斯在1876年首先描述了该几何结构。
构造
拥有二十面体对称五复合立方体可以由以原点为中心、面向轴的第一个立方体开始构造,其余的立方体则透过轴旋转弧度来构造,毕依这加入顺序决定角度值中的n,例如第二个立方体n=1、第三个立方体n=2以此类推。
性质
五复合立方体为五个立方体组合成的形状,因此其边、面和顶点的数量基本上应该会是立方体的5倍,但因为部分顶点是重合的,因此其仅有30个面、60条边和20个顶点。
五复合立方体可以视为正十二面体刻面后的多面体,在正十二面体凸包中每个立方体定位在12个顶点中的其中8个顶点。
 |

|
由于五复合立方体可以看作是在正十二面体中嵌入立方体,因此其顶点坐标与正十二面体相同:
- (±1, ±1, ±1)
- (0, ±1/ϕ, ±ϕ)
- (±1/ϕ, ±ϕ, 0)
- (±ϕ, 0, ±1/ϕ)
其中ϕ = 1 + √5/2为黄金比例。
棱排布
五复合立方体的凸包是正十二面体。其与一些凸包也是正十二面体的多面体有着相同的棱排布,例如小双三斜三十二面体、大双三斜三十二面体和双三斜十二面体。
其他的五个立方体复合图形
亦有其他也由五个立方体组合成的形状,例如佛达里也斯的五复合立方体。这种形状是一个八面体对称的星形多面体。
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.