三体问题 (英语:Three-body problem )是天体力学 中的基本力学模型 。它是指三个质量 、初始位置和初始速度 都是任意的可视为质点的天体,在相互之间万有引力的作用下的运动规律问题。[ 1]
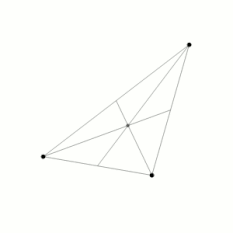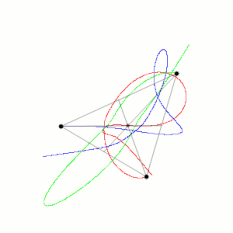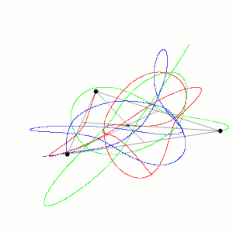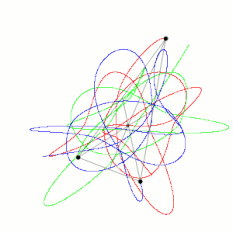
初始位置在斜三角形顶点,且初始速度均为零的三个相同物体的近似轨迹。按照动量守恒定律,质心仍然存在。
三体问题是多体问题的一个特例。对于一般多体问题而言,不存在一般的解析解[ 2]
例如太阳系中,考虑太阳、地球和月球的运动,它们彼此以万有引力相吸引,若假设三个星球都可设为质点,并且忽略其他星球的引力,太阳、地球和月球的运动即可以视为三体问题。
三体问题也被用于模拟经典力学或量子力学中三个粒子的运动状态。
三体问题可以用三个质量为
m
i
{\displaystyle m_{i}}
r
i
=
(
x
i
,
y
i
,
z
i
)
{\displaystyle \mathbf {r_{i}} =(x_{i},y_{i},z_{i})}
牛顿运动方程 数学表示:
{
r
¨
1
=
−
G
m
2
r
1
−
r
2
|
r
1
−
r
2
|
3
−
G
m
3
r
1
−
r
3
|
r
1
−
r
3
|
3
,
r
¨
2
=
−
G
m
3
r
2
−
r
3
|
r
2
−
r
3
|
3
−
G
m
1
r
2
−
r
1
|
r
2
−
r
1
|
3
,
r
¨
3
=
−
G
m
1
r
3
−
r
1
|
r
3
−
r
1
|
3
−
G
m
2
r
3
−
r
2
|
r
3
−
r
2
|
3
.
{\displaystyle {\begin{cases}{\ddot {\mathbf {r} }}_{\mathbf {1} }&=-Gm_{2}{\frac {\mathbf {r_{1}} -\mathbf {r_{2}} }{|\mathbf {r_{1}} -\mathbf {r_{2}} |^{3}}}-Gm_{3}{\frac {\mathbf {r_{1}} -\mathbf {r_{3}} }{|\mathbf {r_{1}} -\mathbf {r_{3}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {2} }&=-Gm_{3}{\frac {\mathbf {r_{2}} -\mathbf {r_{3}} }{|\mathbf {r_{2}} -\mathbf {r_{3}} |^{3}}}-Gm_{1}{\frac {\mathbf {r_{2}} -\mathbf {r_{1}} }{|\mathbf {r_{2}} -\mathbf {r_{1}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {3} }&=-Gm_{1}{\frac {\mathbf {r_{3}} -\mathbf {r_{1}} }{|\mathbf {r_{3}} -\mathbf {r_{1}} |^{3}}}-Gm_{2}{\frac {\mathbf {r_{3}} -\mathbf {r_{2}} }{|\mathbf {r_{3}} -\mathbf {r_{2}} |^{3}}}.\end{cases}}}
G
{\displaystyle G}
万有引力常数 。[ 3] [ 4]
这个问题也可以用哈密顿形式 等价表示,此时可以用一组18个一阶微分方程表示,这些方程分别对应于
r
i
{\displaystyle \mathbf {r_{i}} }
p
i
{\displaystyle \mathbf {p_{i}} }
d
r
i
d
t
=
∂
H
∂
p
i
,
d
p
i
d
t
=
−
∂
H
∂
r
i
,
{\displaystyle {\frac {d\mathbf {r_{i}} }{dt}}={\frac {\partial {\mathcal {H}}}{\partial \mathbf {p_{i}} }},\qquad {\frac {d\mathbf {p_{i}} }{dt}}=-{\frac {\partial {\mathcal {H}}}{\partial \mathbf {r_{i}} }},}
H
{\displaystyle {\mathcal {H}}}
哈密顿量 :
H
=
−
G
m
1
m
2
|
r
1
−
r
2
|
−
G
m
2
m
3
|
r
3
−
r
2
|
−
G
m
3
m
1
|
r
3
−
r
1
|
+
p
1
2
2
m
1
+
p
2
2
2
m
2
+
p
3
2
2
m
3
.
{\displaystyle {\mathcal {H}}=-{\frac {Gm_{1}m_{2}}{|\mathbf {r_{1}} -\mathbf {r_{2}} |}}-{\frac {Gm_{2}m_{3}}{|\mathbf {r_{3}} -\mathbf {r_{2}} |}}-{\frac {Gm_{3}m_{1}}{|\mathbf {r_{3}} -\mathbf {r_{1}} |}}+{\frac {\mathbf {p_{1}} ^{2}}{2m_{1}}}+{\frac {\mathbf {p_{2}} ^{2}}{2m_{2}}}+{\frac {\mathbf {p_{3}} ^{2}}{2m_{3}}}.}
圆型限制性三体问题是太阳系 中椭圆轨道的有效近似,这里可以用两个主天体的引力以及它们旋转的离心效应而产生的电势组合实现可视化(科里奥利效应 是动态的,此处未显示)。然后,可以将拉格朗日点 视为合成表面上梯度为零的五个位置(用蓝线显示),表明此处处于平衡状态。 当所讨论的三个天体中﹐三体中其中两体的质量极大,以至于第三体的质量几乎不能对其造成任何扰动;或是有一个天体的质量与其他两体的质量相比小到可以忽略时,可将三体问题简化为二体问题的变型。这样的三体问题称为限制性三体问题 。[ 3] 无限小质量体 ﹐简称小天体 ;把另外两个大质量的天体称为有限质量体 。
设
m
1
,
2
{\displaystyle m_{1,2}}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
(
x
2
,
y
2
)
{\displaystyle (x_{2},y_{2})}
(
x
,
y
)
{\displaystyle (x,y)}
{
d
2
x
d
t
2
=
−
m
1
x
−
x
1
r
1
3
−
m
2
x
−
x
2
r
2
3
,
d
2
y
d
t
2
=
−
m
1
y
−
y
1
r
1
3
−
m
2
y
−
y
2
r
2
3
.
{\displaystyle {\begin{cases}{\frac {d^{2}x}{dt^{2}}}=-m_{1}{\frac {x-x_{1}}{r_{1}^{3}}}-m_{2}{\frac {x-x_{2}}{r_{2}^{3}}},\\{\frac {d^{2}y}{dt^{2}}}=-m_{1}{\frac {y-y_{1}}{r_{1}^{3}}}-m_{2}{\frac {y-y_{2}}{r_{2}^{3}}}.\end{cases}}}
r
i
=
(
x
−
x
i
)
2
+
(
y
−
y
i
)
2
.
{\displaystyle r_{i}={\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}}}.}
在此数学表示中,运动方程通过坐标
x
i
(
t
)
,
y
i
(
t
)
{\displaystyle x_{i}(t),y_{i}(t)}
1499年,韦斯普奇 最早提出三体问题。他利用月球位置讯息来确定自己在巴西的位置。[ 5] 约翰·哈里森 发明的航海经线仪解决了确定经度的问题。但是,由于太阳和行星对月球绕地公转的扰动效应,月球理论的准确性很低。
亚美利哥·韦斯普奇 和伽利略·伽利莱 随后也提出了三体问题。伽利略确定所有天体的下落速度都是相同均匀的,但他并没有将其应用到行星运动。[ 6]
1687年,当时艾萨克·牛顿 发表了《自然哲学的数学原理》 。在《原理》第一卷的第66号命题及其22个推论中,牛顿首次定义和研究了三个受相互扰动的重力吸引影响的巨大物体的运动问题。在第三册的第25至35条命题中,牛顿将他的66号命题结果用于月球在地球和太阳的引力影响下的运动。[ 7]
让·勒朗·达朗贝尔 和亚历克西·克洛德·克莱罗 两个长期竞争者都试图找到该问题的某种通性。他们竞相在1747年向法国皇家科学研究院提交了他们的第一批三体问题分析。“三体问题”(法语:Problème des trois Corps)这个名字至此开始广泛使用。达朗贝尔于1761年发布的文章表明,该名称最早使用于1747年。
1887年,为了祝贺自己的60岁寿诞,瑞典国王 奥斯卡二世 赞助了一项现金奖励的竞赛,征求太阳系的稳定性问题的解答,这是三体问题 的一个变型。
法国数学家亨利·庞加莱 简化了问题,提出了限制性三体问题:即三体中其中两体的质量极大,以至于第三体的质量完全不能对其造成任何扰动。面对这个问题,庞加莱运用了他发明的相图 理论,并且最终发现了混沌理论 。虽然庞加莱没有成功给出一个完整的解答,不过他的工作令人印象深刻,因此他于1888年赢得了奖金。
庞加莱 发现这个系统的演变经常是混沌的,即如果初始状态有一个小的扰动,例如个体的初始位置有一个小的变动,则后来的状态可能会有极大的不同。如果这一小变动不能被测量仪器所探测,那么我们将不能预测最终状态为何。
著名数学家兼竞赛裁判卡尔·魏尔施特拉斯 说:“这个工作不能真正视为对所求的问题的完善解答,但是它的重要性使得它的出版将标志着天体力学的一个新时代的诞生。”
魏尔斯特拉斯 并不知道他自己的预测有多准确。在庞加莱的论文中,他描述了例如同宿点 《数学学报》 混沌理论 的开端。
19世纪末到20世纪初,科学家们研究使用短程二体吸力来解决三体问题的方法。19世纪后期,乔治·威廉·希尔 在用金星和水星的运动来研究限制性三体问题,不久进一步延伸到四体问题以计算月球绕地球轨道和行星环绕恒星轨道。
1907年[ 8] [ 9] 卡尔·弗里肖夫·松德曼 t 1/3 勒贝格测度 为0时才会出现)外,对所有实数t始终收敛。松德曼的研究成果收录于1912年的瑞典《数学学报》 上[ 10]
1930年,数学家大卫·贝洛里奇 (David Beloriszky)指出,松德曼级数收敛极慢,如果将松德曼级数解用于天文观测,则计算有效项数将至少达到107006800000000000000♠ 8000 000 [ 11]
1970年,前苏联理论物理学家维塔利·尼古拉耶维奇·叶菲莫夫 预测当三个相同的玻色子之间的对相互作用接近共振时,三体谱表现出无限的束缚态序列。这一预测于2006年证实,因此也称为叶菲莫夫效应 [ 12]
20世纪70年代,米歇尔·赫农 罗杰A.布鲁克 [ 13]
1979年,前苏联数学家L·K·巴巴德赞詹兹 (LK Babadzanjanz)发表论文《Existence of the continuations in the N-body problem(多体问题连续性的存在性)》[ 14] [ 15]
1985年,中国数学家汪秋栋 发表论文《多体问题全局解的存在性》
[ 16] [ 17]
三体问题在单周期T≃6.3259时的“8”字型解动画。[ 18] 1993年,圣塔菲研究所的美国物理学家克里斯·摩尔 [ 19] 阿兰·契纳 理查德·蒙哥马利 (Richard Montgomery)证明。
[ 20] [ 21]
2013年,贝尔格莱德物理研究所的物理学家米洛万·乌瓦科夫 (Milovan Šuvakov)与维利科·德米特拉·伊诺维 (Veljko Dmitrašinović)发现了等质量零角动量三体问题的13种新的解族。
[ 2] [ 13]
2015年,物理学家安娜·胡多马尔 (Ana Hudomal)发现了14种等质量零角动量三体问题的新解族。
[ 22]
2017年,中国计算机科学家李晓明 和中国数学家廖世俊 发现了669组等质量零角动量三体问题的新周期轨道。
[ 23] [ 24]
2018年,李晓明 和廖世俊 发布了234个不等质量“自由落体”三体问题的解。三体问题的自由落体公式从所有三个静止的物体开始。正因为如此,质量在一个自由落体配置不在一个闭合的“循环”轨道上运行,而是沿着一个开放的“轨道”向前和向后运行。
[ 25]
2019年,爱丁堡大学菲利普·布林 (Philip Breen)等人训练了一种用于三体问题的快速神经网络。[ 26]
2022年,廖世俊 、杨宇 和李晓明 在《新天文学》 [ 27]
2023年,伊万·赫里斯托夫 (Ivan Hristov)、拉多斯拉娃·赫里斯托娃 (Radoslava Hristova)、维利科·德米特拉希诺维奇 (Veljko Dmitrašinović)和谷川清隆 (Kiyotaka Tanikawa)发表了一篇关于等质量三体系统的周期轨道研究,发现了12409个不同轨道。[ 28]
由三个物体相互作用 构成的引力系统是混沌系统,不过由三个物体弹性相互作用构成的系统则不然。 三体序列的收敛半径由到最近奇点的距离决定。因此,必须要考虑三体问题的可能奇点。三体问题中的唯二奇点是二元碰撞(两个天体间的瞬时碰撞)和三元碰撞(三个天体间的瞬时碰撞),下面对此类状态进行简单讨论。
实际上多体间不太可能发生碰撞(包括二体和三体),因为此前已证明碰撞状态对应勒贝格测度 为0的一组初始状态。然而,由于没有对这一初始状态进行研究,以避免相应解出现碰撞奇点。因此,松德曼的求解思路包含以下几大要点:
通过适当的变量替换,用正则化 去分析二元碰撞以外的解。
用保罗·潘勒韦方程
证明如果L≠0,则不仅不存在三元碰撞,而且系统严格有界远离三元碰撞。通过对微分方程使用柯西存在性定理,证明在以实轴为中心的复平面(符合柯西—柯瓦列夫斯卡娅定理
构造保角变换h(z)=
e
π
ω
2
Ω
{\displaystyle e^{\frac {\pi \omega }{2\Omega }}}
ω = t 1/3 | ω - ω* | ≤ Ω
{
ω
=
2
Ω
π
l
o
g
1
+
τ
1
−
τ
,
τ
=
e
π
ω
2
Ω
−
1
e
π
ω
2
Ω
+
1
.
{\displaystyle {\begin{cases}\omega ={\frac {2\Omega }{\pi }}log{1+\tau \over 1-\tau },\\\tau ={\frac {e^{\frac {\pi \omega }{2\Omega }}-1}{e^{\frac {\pi \omega }{2\Omega }}+1}}.\end{cases}}}
[ 29]
1985年,中国数学家汪秋栋 发表论文《多体问题全局解的存在性》[ 16] [ 17]
20组三体问题周期性特解示例。 1767年,莱昂哈德·欧拉 提出了三个周期解序列,其中三个物体在任意时刻均共线。具体内容参见欧拉三体问题
1772年,拉格朗日 找到了一系列由三个质点组成的等边三角形解。这些解与欧拉的共线解一起构成了三体问题的中心构形 开普勒椭圆 运动。这四个解族是唯一有明确解析式的已知解族。在圆型限制性三体问题的特殊情况下,这些解在随原点变换的旋转坐标轴中称为拉格朗日点 L1 , L2 , L3 , L4 和L5 ,其中L3 , L4 是拉格朗日对称解的实例。
1892年至1899年,庞加莱 为限制性三体问题找到了一组无穷多的周期解,并将这组解推广至一般三体问题。
1893年,恩斯特·迈塞尔 卡尔·伯劳 [ 30]
1967年,维克多·塞贝赫利 弗雷德里克·彼得斯 (C. Frederick Peters)利用数值积分理论建立了这个问题的最终逃逸模型,同时找到了附近的周期解。
[ 31]
20世纪70年代,米歇尔·赫农 和罗杰A.布鲁克 分别找到了一套特殊解族,这些特殊解族构成了同系列特殊解族: 布鲁克-赫农-哈德吉德梅特里奥解族 。在这一解族中,这三个物体都具有相同的质量,可以表现出逆行和直行两种形式。在布鲁克的一些解中,两个物体延相同的轨道运行。[ 13]
尽管高精度需要大量的CPU时间,但是可以用数值积分在计算机上得到多体问题的任意高精度解。现已有人尝试创建计算机程序,结合狭义相对论等现代物理学理论,以数字方式解决涉及电磁相互作用和引力相互作用的三体问题(以及扩展的多体问题)。此外,使用随机游走 理论,可以计算三体处于不同位置的概率。
2017年,廖世俊 和李晓明 发明了“精准数值模拟(the clean numerical simulation,CNS)”的混沌系统数值模拟新策略,用超级计算机成功获得了695个等质量三体系统的周期轨道。[ 32]
2019年,布林 等人训练了一种用于三体问题的快速神经网络,该神经网络使用数字积分器进行训练。[ 26]
2023年,伊万·赫里斯托夫 、拉多斯拉娃·赫里斯托娃 、维利科·德米特拉希诺维奇 和谷川清隆 发表了一篇关于等质量三体系统的周期轨道研究。其中,他们发现了12409个不同轨道。[ 28]
三体问题是多体问题的一个特例,它描述了多个物体如何在一种相互作用(如引力)下移动。这些问题具有收敛幂级数形式的全局解析解,正如松德曼(n = 3)和汪秋栋(n >3)所证明的那样(详见N体问题)。然而,松德曼-汪秋栋级数收敛得如此之慢,以至于它们没有什么实用性。[ 33] 数值分析 方法求取近似解,或在某些特殊情况下,使用经典三角级数 近似(参见多体模拟)。原子系统,例如原子、离子和分子,可以用量子多体问题来处理。在经典力学系统中,多体系统通常是指一个星系或星系团 ;行星系统,如恒星、行星及其卫星等也可视为多体系统。一部分可以用扰动 理论简化处理,其中系统被视为二体系统加上一个假定导致偏离无扰动双体轨迹的额外力。
中国作家刘慈欣 围绕三体问题展开创作了《三体》三部曲中的第一部作品《三体》,向公众科普了三体问题。
[ 34] [ 35]
Barrow-Green, June. The Three-Body Problem. Gowers, Timothy; Barrow-Green, June; Leader, Imre (编). The Princeton Companion to Mathematics. Princeton University Press: 726–728. 2008.
Sundman, Karl F. Recherches sur le problème des trois corps. Acta Societatis Scientiarum Fennicæ.
Sundman, Karl F. Nouvelles recherches sur le problème des trois corps. Acta Societatis Scientiarum Fennicæ.
Beloriszky, D. Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps. Bulletin Astronomique. Série 2. 1930, 6 : 417–434. Bibcode:1930BuAst...6..417B Here the gravitational constant G has been set to 1, and the initial conditions are r 1 (0) = -r 3 (0) = (-0.97000436, 0.24308753); r 2 (0) = (0,0); v 1 (0) = v 3 (0) = (0.4662036850, 0.4323657300); v 2 (0) = (-0.93240737, -0.86473146). The values are obtained from Chenciner & Montgomery (2000).
Li, Xiaoming; Jing, Yipeng; Liao, Shijun. The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum. Publications of the Astronomical Society of Japan. August 2018, 70 (4): 64. arXiv:1709.04775 doi:10.1093/pasj/psy057 Breen, Philip G.; Foley, Christopher N.; Boekholt, Tjarda; Portegies Zwart, Simon. Newton versus the machine: Solving the chaotic three-body problem using deep neural networks. Monthly Notices of the Royal Astronomical Society. 2020, 494 (2): 2465–2470. S2CID 204734498 arXiv:1910.07291 doi:10.1093/mnras/staa713 李晨阳 张双虎. 求解“三体问题”的中国科学家 . 报纸 (中国科学报). 中国科学报. 2022-07-27 [2023-06-22 ] . (原始内容存档 于2023-06-22). Hristov, Ivan; Hristova, Radoslava; Dmitrašinović, Veljko; Tanikawa, Kiyotaka. Three-body periodic collisionless equal-mass free-fall orbits revisited. 2023. arXiv:2308.16159 physics.class-ph ].
Aarseth, S. J. Gravitational n-Body Simulations . New York: Cambridge University Press. 2003. ISBN 978-0-521-43272-6 Bagla, J. S. Cosmological N-body simulation: Techniques, scope and status. Current Science . 2005, 88 : 1088–1100. Bibcode:2005CSci...88.1088B arXiv:astro-ph/0411043 Chambers, J. E.; Wetherill, G. W. Making the Terrestrial Planets: N-Body Integrations of Planetary Embryos in Three Dimensions. Icarus . 1998, 136 (2): 304–327. Bibcode:1998Icar..136..304C CiteSeerX 10.1.1.64.7797 doi:10.1006/icar.1998.6007 Efstathiou, G.; Davis, M.; White, S. D. M.; Frenk, C. S. Numerical techniques for large cosmological N-body simulations . Astrophysical Journal . 1985, 57 : 241–260. Bibcode:1985ApJS...57..241E doi:10.1086/191003 Hulkower, Neal D. The Zero Energy Three Body Problem. Indiana University Mathematics Journal . 1978, 27 (3): 409–447. Bibcode:1978IUMJ...27..409H doi:10.1512/iumj.1978.27.27030 Hulkower, Neal D. Central Configurations and Hyperbolic-Elliptic Motion in the Three-Body Problem. Celestial Mechanics . 1980, 21 (1): 37–41. Bibcode:1980CeMec..21...37H S2CID 123404551 doi:10.1007/BF01230244 Li, Xiaoming; Liao, Shijun. On the stability of the three classes of Newtonian three-body planar periodic orbits. Science China Physics, Mechanics & Astronomy . 2014, 57 (11): 2121–2126. Bibcode:2014SCPMA..57.2121L S2CID 73682020 arXiv:1312.6796 doi:10.1007/s11433-014-5563-5 Moore, Cristopher. Braids in Classical Dynamics (PDF) . Physical Review Letters. 1993, 70 (24): 3675–3679 [2016-01-01 ] . Bibcode:1993PhRvL..70.3675M PMID 10053934 doi:10.1103/PhysRevLett.70.3675 原始内容 (PDF) 存档于2018-10-08). Poincaré, H. New Methods of Celestial Mechanics ISBN 978-1-56396-117-5 Šuvakov, Milovan; Dmitrašinović, V. Three Classes of Newtonian Three-Body Planar Periodic Orbits. Physical Review Letters . 2013, 110 (10): 114301. Bibcode:2013PhRvL.110k4301S PMID 25166541 S2CID 118554305 arXiv:1303.0181 doi:10.1103/PhysRevLett.110.114301