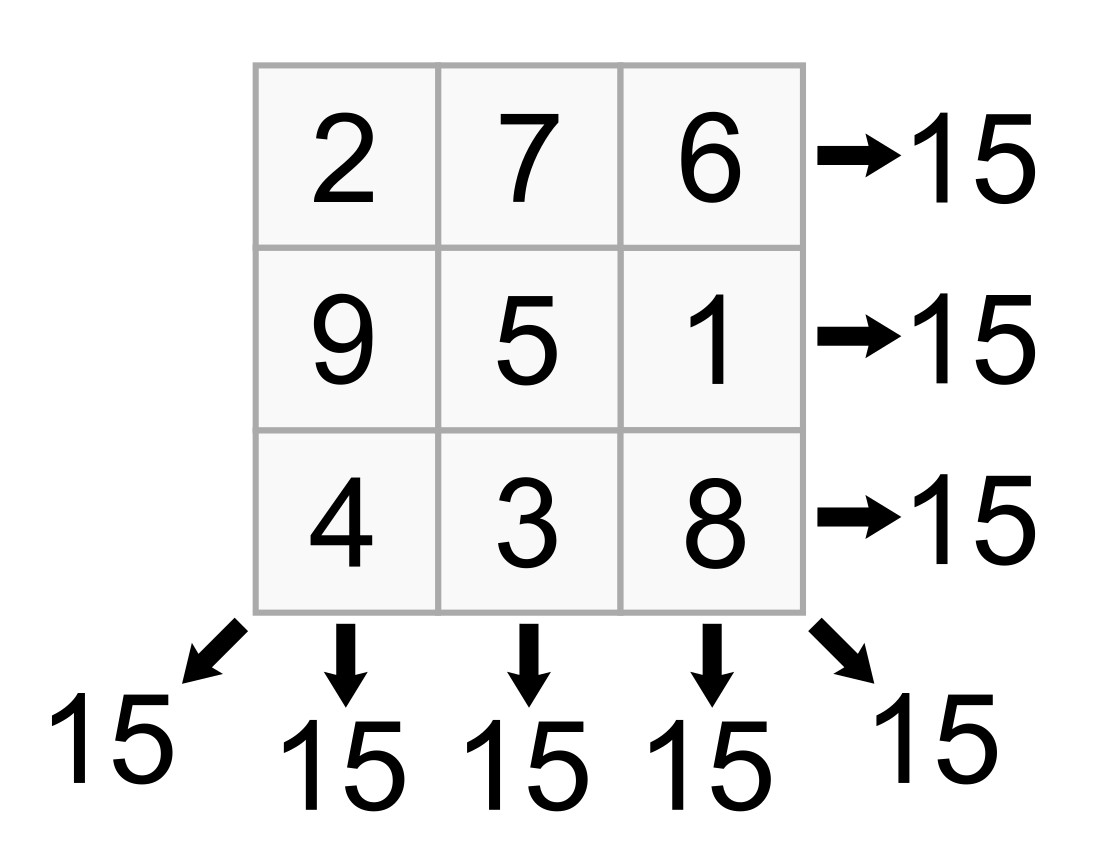
Trong toán vui, một ma trận kì ảo bậc n (còn gọi là ma phương hay hình vuông ma thuật) là một cách sắp xếp n² số, thường là các số nguyên phân biệt, trong một bảng vuông sao cho tổng n số trên mỗi hàng, cột, và đường chéo đều bằng nhau.[1] Ma trận kì ảo chuẩn chứa các số nguyên từ 1 đến n².
Tồn tại ma trận kì ảo chuẩn cho mọi bậc n ≥ 1 trừ n = 2. Ma trận kì ảo bậc 1 là trường hợp tầm thường, nó chứa duy nhất một ô với giá trị 1. Trường hợp không tầm thường có kích thước nhỏ nhất là ma trận kì ảo bậc 3.
Hằng số là tổng của mỗi hàng, cột, và đường chéo được gọi là hằng số kì ảo. Giá trị này của ma trận kì ảo chuẩn chỉ phụ thuộc vào n và có giá trị
Với các ma trận kì ảo bậc n = 3, 4,5, ..., các hằng số kì ảo tương ứng là:
15, 34, 65, 111, 175, 260, ... (chuỗi A006003 trong từ điển bách khoa về các chuỗi số nguyên OEIS).
Steve Wozniak, người đồng sáng lập Apple Inc., xây dựng một ma trận kì ảo sau khi đề nghị người xem đưa ra một số ngẫu nhiên để làm hằng số kì ảo. Hình chụp tại Macworld Expo 2009.Chi tiết của Melencolia IMột ma trận kỳ ảo trên chính diện của Nhà thờ Sagrada Família.
Các nhà toán học Trung Hoa đã biết đến ma trận kì ảo (ma phương) từ năm 650 trước Công Nguyên[2]. Thế kỉ thứ 7, người Ả Rập đã học được ma trận kì ảo từ người Ấn Độ. Những ma trận kì ảo bậc 5 và 6 đầu tiên xuất hiện trong một cuốn bách khoa toàn thư của thành Baghdad vào khoảng năm 983 (Rasa'il Ihkwan al-Safa); một số nhà toán học Ả Rập thời kì trước đó đã biết đến những ma trận kì ảo đơn giản hơn.[2].
Hình vuông kì lạ này (còn gọi là ma phương) được người Trung Quốc phát minh khoảng 4 hoặc 5 nghìn năm trước công nguyên[cần dẫn nguồn]. Trong tài liệu thời đó thì số 2 được ghi •—• (hình tròn đen chỉ số chẵn, còn gọi là nữ số) số 3 được ghi o—o—o (hình tròn trắng chỉ số lẻ, còn gọi là nam số).
4
9
2
3
5
7
8
1
6
Đến thế kỷ I sau công nguyên, người Ấn Độ lại phát minh ra hình vuông kỳ lạ lớn hơn gồm 4*4 ô.
1
14
15
4
12
7
6
9
8
11
10
5
13
2
3
16
Ở đây 16 số từ 1 đến 16 được sắp xếp trong 16 ô và có tính chất như hình vuông 9 ô của người Trung Quốc.
Hình vuông kỳ lạ này xuất hiện ở châu Âu vào thế kỷ thứ XV. Đến năm 1514, nhà điêu khắc, hội họa kiêm toán học người Đức là A. Đua-re (Durer) đã ghi hình vuông kỳ lạ của người Ấn Độ vào một tác phẩm điêu khắc của mình: "Mêlăngcôli".
Hình vuông của Ấn Độ còn có thêm 6 tính chất đặc biệt sau:
Tổng 4 số ở bốn góc 1+4+16+13=34.
Tổng các số trong bốn hình vuông nhỏ ở giữa (cũng gồm 4 ô vuông) đều bằng 34:
1+14+12+7=34
8+11+13+2=34
10+5+3+16=34
15+4+6+9 =34
7+6+11+10=34
Ở mỗi hàng ngang cặp số đầu có tổng là 15, cặp số sau có tổng là 19 hoặc ngược lại.
Tổng bình phương các số thuộc hàng ngang thứ nhất và thứ tư bằng nhau, tương tự với tổng bình phương các số thuộc hàng ngang thứ hai và thứ ba:
12+142+152+42=132+22+32+162=438
122+72+62+92=82+112+102+52=310
Tổng bình phương các số thuộc hàng dọc thứ nhất và thứ tư bằng nhau, tương tự với tổng bình phương các số thuộc hàng dọc thứ hai và ba:
12+122+82+132=42+92+52+162=378
142+72+112+22=152+62+102+32=370
Nếu nối trung điểm các cạnh của hình vuông ta được một hình vuông nội tiếp.Ta thấy rằng: Tổng các số ở hai cạnh đối này bằng tổng các số ở hai cạnh đối kia: 12+14+3+5=15+9+8+2=34; Tổng bình phương và tổng lập phương các số này cũng bằng nhau.
Loại 3*3 (lẻ):
4
9
2
4
9
2
3
5
7
3
5
7
8
1
6
8
1
6
4
9
2
4
9
2
3
5
7
3
5
7
8
1
6
8
1
6
Chọn một ô ở giữa của một cạnh bất kì trong hình vuông.
Ba số liên tiếp được viết theo đường chéo. Khi kết thúc, từ số cuối của dãy đó đi lên một ô rồi lại viết theo đường chéo với ba sô liên tiếp tiếp theo.
Quy tắc trên cũng được áp dụng với các hình vuông có độ dài các cạnh là số lẻ tiếp theo.
.jpg)
