Kinh tế lượng

Kinh tế lượng (Tiếng Anh: econometrics) là một bộ phận của Kinh tế học, được hiểu theo nghĩa rộng là môn khoa học kinh tế giao thoa với thống kê học và toán kinh tế.^[1] Hiểu theo nghĩa hẹp, là ứng dụng toán, đặc biệt là các phương pháp thống kê vào kinh tế.^[2] Kinh tế lượng lý thuyết nghiên cứu các thuộc tính thống kê của các quy trình kinh tế lượng, ví dụ như: xem xét tính hiệu quả của việc lấy mẫu, của thiết kế thực nghiệm... Kinh tế lượng thực nghiệm bao gồm: (1)ứng dụng các phương pháp kinh tế lượng vào đánh giá các lý thuyết kinh tế (2) phát triển và sử dụng các mô hình kinh tế lượng, tất cả để sử dụng vào nghiên cứu quan sát kinh tế trong quá khứ hay dự đoán tương lai. Thuật ngữ Kinh tế lượng (econometrics) lần đầu tiên được sử dụng vào năm 1910 bởi Paweł Ciompa.^[3]

Bài viết này trong loại bài Kinh tế học
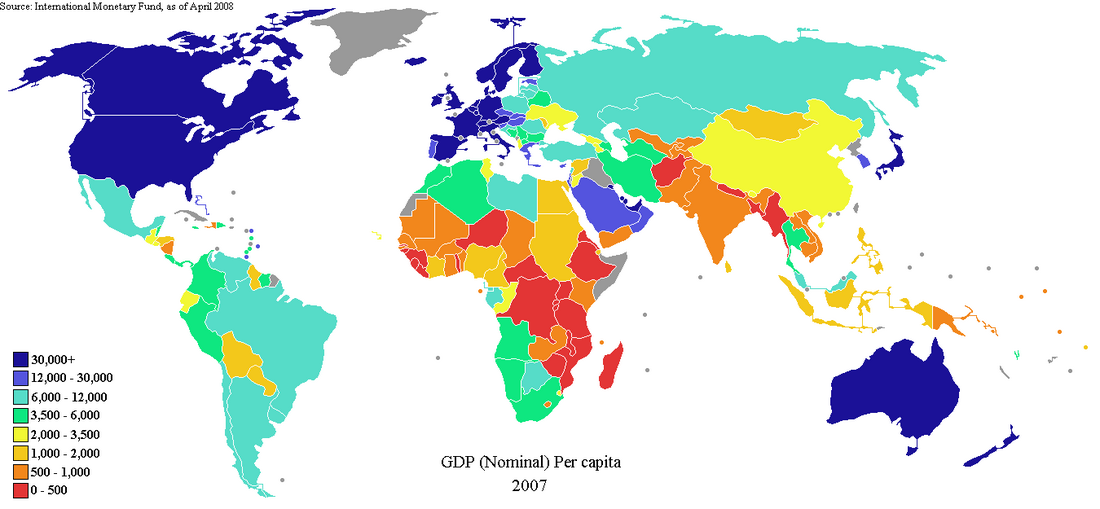
Các nền kinh tế theo vùng  Châu Phi · Bắc Mỹ Nam Mỹ · Châu Á Châu Âu · Châu Đại Dương
Đề cương các chủ đề
Phân loại tổng quát
Kinh tế học vi mô · Kinh tế học vĩ mô Lịch sử tư tưởng kinh tế Lý luận · Các phương pháp không chính thống
Các phương pháp kỹ thuật
Toán học · Kinh tế lượng Thực nghiệm · Kế toán quốc gia
Lĩnh vực và tiểu lĩnh vực
Hành vi · Văn hóa · Tiến hóa Tăng trưởng · Phán triển · Lịch sử Quốc tế · Hệ thống kinh tế Tiền tệ và Tài chính Công cộng và Phúc lợi Sức khỏe · Nhân lực · Quản lý Quản trị · Thông tin · Tổ chức · Lý thuyết trò chơi Lý thuyết tổ chức ngành · Luật pháp Nông nghiệp · Tài nguyên thiên nhiên Môi trường · Sinh thái Đô thị · Nông thôn · Vùng
Danh sách
Tạp chí · Ấn bản Phân loại · Các chủ đề · Kinh tế học gia
Các tư tưởng kinh tế  Vô chính phủ · Tư bản cộng sản · Tập đoàn Phát-xít · Gióc-giơ Hồi giáo · Laissez-faire Chủ nghĩa xã hội thị trường · Trọng thương Bảo hộ · Xã hội Chủ nghĩa công đoàn · Con đường thứ ba
Các nền kinh tế khác  Ăng-lô - Xắc-xông · Phong kiến Toàn cầu · Săn bắn-hái lượm Nước công nghiệp mới Cung điện · Trồng trọt Hậu tư bản · Hậu công nghiệp Thị trường xã hội · Thị trường chủ nghĩa xã hội Token · Truyền thống Thông tin · Chuyển đổi
Chủ đề Kinh tế học
Hộp này: view talk edit

Kinh tế lượng khác với các nhánh khác của thống kê học ở chỗ econometrics đặc biệt liên quan tới các nghiên cứu quan sát và với hệ thống các phương trình (equations). Nghiên cứu quan sát khác với nghiên cứu sử dụng thí nghiệm có kiểm soát (vốn hay dùng trong y học hay vật lý).

Mục đích

Hai mục đích chính của kinh tế lượng là (1) kiểm nghiệm lý thuyết kinh tế bằng cách xây dựng các mô hình kinh tế (mà có khả năng kiểm định được) và (2) chạy (estimate) và kiểm tra các mô hình đó xem chúng đưa ra kết quả chấp nhận hay phủ quyết lý thuyết kinh tế.

Ví dụ, một lý thuyết kinh tế cho rằng một đường cầu phải dốc xuống. Người tiêu dùng sẽ mua ít hàng hơn khi giá tăng, giả định rằng các yếu tố khác không đổi để từ đó phong tỏa chỉ kiểm tra mối quan hệ giữa giá và lượng. Một phương trình toán học có thể được viết ra mô tả quan hệ giữa lượng, giá, và các biến (variable) khác như thu nhập, và một random term ε để phản ánh mô hình lý thuyết một cách đơn giản:

${\displaystyle Q=\beta _{0}+\beta _{1}{\text{Price}}+\beta _{2}{\text{Income}}+\varepsilon .}$

Phân tích hồi quy có thể được sử dụng để ước lượng (estimate) các thông số ${\displaystyle \beta _{0}}$, ${\displaystyle \beta _{1}}$, và ${\displaystyle \beta _{2}}$ trong phương trình trên, sử dụng dữ liệu về giá, thu nhập và lượng cầu. Mô hình có thể sau đó được kiểm định về ý nghĩa thống kê statistical significance theo đó tăng giá làm giảm lượng cầu. Giả thuyết để kiểm định ở đây là ${\displaystyle \beta _{1}<0}$.

Phương pháp

Phương pháp thống kê quan trọng nhất trong môn kinh tế lượng là phân tích hồi quy (regression analysis). Phương pháp này quan trọng đối với kinh tế lượng bởi vì các nhà kinh tế không có cơ hội tiến hành các thử nghiệm có kiểm soát. Vấn đề các dữ liệu quan sát chệch do thiếu biến và các vấn đề khác cũng cần phải được giải quyết về mặt thống kê nhờ các mô hình kinh tế lượng. Các nhà kinh tế lượng thường tìm cách làm sáng tỏ các thực nghiệm tự nhiên trong khi thiếu bằng chứng từ các thực nghiệm có kiểm soát.

Cơ sở dữ liệu áp dụng trong kinh tế lượng được chia thành chuỗi thời gian (time series), dữ liệu chéo (cross-sectional analysis), dữ liệu mảng (panel data) và dữ liệu mảng đa chiều. Chuỗi thời gian là tập hợp những quan sát của một biến số (ví dụ tỷ lệ lạm phát) trong những khoảng thời gian liên tiếp nhau (ví dụ trong 20 năm). Cơ sở dữ liệu cross-sectional là những quan sát của nhiều cá nhân trên một đặc tính (ví dụ thu nhập) tại cùng một thời điểm duy nhất (ví dụ thu nhập của 1000 người trong mẫu vào cuối năm 2011). Cơ sở dữ liệu mảng (panel data) chứa cả quan sát của chuỗi thời gian và của cross-sectional. Vì vậy, panel data thường được hiểu là dữ liệu hai chiều. Dữ liệu mảng đa chiều là tập hợp các quan sát theo dạng mảng, theo thời gian và cả theo một số chiều thứ ba nữa. Ví dụ Cơ sở dữ liệu của Nghiên cứu hộ gia đình, bao gồm rất nhiều chiều (thu nhập, tình trạng sức khỏe, trình độ học vấn...) theo thời gian.

Phân tích kinh tế lượng còn có thể phân loại dựa trên số lượng các quan hệ được mô hình hóa. Phương pháp phương trình đơn mô hình hóa một biến số duy nhất, gọi là (biến phụ thuộc), dưới dạng một hàm số mà đầu vào là một hay nhiều biến độc lập. Trong nhiều trường hợp, phương pháp Bình phương tối thiểu không thể thể hiện được quan hệ cần nghiên cứu, hoặc có thể tạo ra các ước lượng sai, bởi các giả thuyết để chạy được mô hình nhiều khi bị vi phạm. Một cách khắc phục đó là sử dụng instrumental variables (IV). Khi mô hình bao gồm nhiều phương trình, thì cácphương pháp phương trình đồng thời (simultaneous-equation methods) có thể được sử dụng, bao gồm two IV variants, Two-Stage Least Squares (2SLS), và Three-Stage Least Squares (3SLS).

Các phương pháp ước lượng khác gồm Method of Moments, Generalized Method of Moments (GMM), phân tích chuỗi thời gian (time series analysis), và các phương pháp Bayesian.

Ví dụ

Một ví dụ đơn giản là tìm mối quan hệ trong kinh tế lượng trong lĩnh vực kinh tế lao động:

${\displaystyle \ln({\text{wage}})=\beta _{0}+\beta _{1}({\text{years of education}})+\varepsilon .}$

Ví dụ này giả sử rằng logarit tự nhiên của lương của một người là một hàm tuyến tính với biến đầu vào là số năm học của người đó. Tham số ${\displaystyle \beta _{1}}$ đo mức tăng lên của logarit tự nhiên (ln) của lương bắt nguồn từ một năm học tăng thêm. ${\displaystyle \epsilon }$ là một biến ngẫu nhiên (random variable) đại diện cho tất cả các yếu tố khác có thể ảnh hưởng đến lương. Mục tiêu ở đây là ước lượng các thông số, ${\displaystyle \beta _{0}{\mbox{ và }}\beta _{1}}$ với các giả thuyết về biến ngẫu nhiên ${\displaystyle \epsilon }$. Ví dụ, nếu ${\displaystyle \epsilon }$ không tương quan (uncorrelated) (hay còn gọi là độc lập) với số năm học, thì phương trình trên có thể được ước lượng bằng phương pháp hồi quy tuyến tính (linear regression) hay còn gọi là ordinary least squares.

Tuy nhiên, trên thực tế câu chuyện không đơn giản như vậy. Có thể xem thêm phần tiếng Anh để hiểu thêm tại sao không đơn giản như vậy. Tóm tắt các phương pháp để giải quyết bài toán trên có thể tìm thấy ở Card (1999)^[4].

Các học giả từng đoạt giải Nobel kinh tế do những đóng góp trong môn kinh tế lượng

• Jan Tinbergen và Ragnar Frisch (1969)
• Lawrence Klein (1980)
• Trygve Haavelmo (1989)
• Daniel McFadden và James Heckman (2000)
• Robert Engle và Clive Granger (2003)
• Thomas J.Sargent and Christopher A.Sims (2011)

Tham khảo

1. M. Hashem Pesaran (1987). "Econometrics," The New Palgrave: A Dictionary of Economics, v. 2, p. 8 [pp. 8-22]. Reprinted in J. Eatwell et al., eds. (1990). Econometrics: The New Palgrave, p. 1 [pp. 1-34]. Abstract (2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran).
2. P. A. Samuelson, T. C. Koopmans, and J. R. N. Stone (1954). "Report of the Evaluative Committee for Econometrica," Econometrica 22(2), p. 142. [p p. 141-146], as described and cited in Pesaran (1987) above.
3. “Bản sao đã lưu trữ”. Bản gốc lưu trữ ngày 2 tháng 5 năm 2014. Truy cập ngày 18 tháng 2 năm 2017.
4. David Card (1999) "The Causal Effect of Education on Earning," in Ashenfelter, O. and Card, D., (eds.) Handbook of Labor Economics, pp 1801-63.

Xem thêm

• Chuỗi thời gian
• Panel data
• Hội Kinh tế lượng
• Econometrica
• Huy chương Frisch