Công thức bậc hai

Trong đại số sơ cấp, công thức bậc hai là một công thức cung cấp (các) đáp số cho một phương trình bậc hai. Có nhiều cách khác để giải phương trình bậc hai thay vì dùng công thức bậc hai, chẳng hạn như phân tích thành nhân tử (phân tích trực tiếp, nhóm hạng tử, phương pháp AC), phần bù bình phương, vẽ đồ thị và vân vân.^[1]

Một phương trình bậc hai với các nghiệm x = 1 và x = 4.

Cho một phương trình bậc hai tổng quát có dạng

${\displaystyle ax^{2}+bx+c=0}$

với ${\displaystyle x}$ đại diện cho một ẩn số, ${\displaystyle a}$, ${\displaystyle b}$ và ${\displaystyle c}$ đại diện cho các hằng số với ${\displaystyle a\neq 0}$, công thức bậc hai là:

$${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ }$$

với dấu cộng-trừ "±" chỉ ra rằng phương trình bậc hai có hai nghiệm.^[2] Khi viết riêng ra, chúng trở thành:

${\displaystyle x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{and}}\quad x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}$

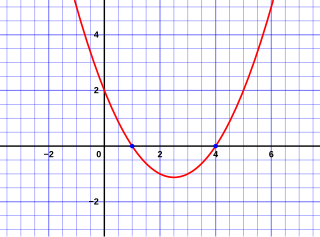
Mỗi nghiệm cũng được gọi là một gốc (hoặc không điểm) của phương trình bậc hai. Về mặt hình học, các gốc này biểu diễn các giá trị ${\displaystyle x}$ mà tại bất kì parabol nào, được cho một cách rõ ràng dưới dạng ${\displaystyle y=ax^{2}+bx+c}$, cắt trục ${\displaystyle x}$ hay trục hoành.^[3]

Cũng như là một công thức sinh ra các không điểm của bất kì parabol nào, công thức bậc hai cũng có thể được sử dụng để nhận biết trục đối xứng của parabol,^[4] và số không điểm thực mà phương trình bậc hai chứa đựng.^[5]

Xem thêm

• Biệt thức
• Định lý cơ bản của đại số
• Phương trình bậc ba

Tham khảo

1. “Quadratic Factorisation: The Complete Guide”. Math Vault (bằng tiếng Anh). ngày 13 tháng 3 năm 2016. Truy cập ngày 10 tháng 11 năm 2019.
2. Sterling, Mary Jane (2010), Algebra I For Dummies, Wiley Publishing, tr. 219, ISBN 978-0-470-55964-2
3. “Understanding the quadratic formula”. Khan Academy (bằng tiếng Anh). Truy cập ngày 10 tháng 11 năm 2019.
4. “Axis of Symmetry of a Parabola. How to find axis from equation or from a graph. To find the axis of symmetry...”. www.mathwarehouse.com. Truy cập ngày 10 tháng 11 năm 2019.
5. “Discriminant review”. Khan Academy (bằng tiếng Anh). Truy cập ngày 10 tháng 11 năm 2019.