Вейвлет

Вейвлети — це родина математичних функцій, яка допомагає аналізувати частотні компоненти сигналів (функцій залежних від часу), методами схожими на перетворення Фур'є — Вейвлет-перетворення. Вейвлети надають ортогональний базис, який також має частотну характеристику, але на відміну від нескінчених коливань осциляторних функцій для перетворення Фур'є, коливання вейвлетів локалізовані в просторі. Це означає що амплітуда (енергія) сконцентрована на скінченому інтервалі, та швидко затухає за межами визначеної інтервалу, або області у випадку багатовимірних функції.

Приклад вейвлет-функції, амплітуда якої локалізована навколо значення 4,5 та затухає за межами деякого інтервалу

Етимологія

Слово вейвлет походить від французького ondelette — маленька хвиля, яке перекладено англійською як wavelet (англ. wave — хвиля, та зменшувального суфіксу -let). Термін впроваджений французьким геофізиком Жаном Морле (Jean Morlet) та разом з Алексом Гросманом (Alex Grossmann), та використовується з 50х років в геофізиці^[1].Таким чином можна перекласти як хвилька, тобто маленька хвиля. І хоча деякі мови перекладають це слово, як наприклад іспанське Ondícula або польське Falki, в інших мовах використовують транслітерацію слова вейвлет.

Застосування вейвлет-перетворень

Частотна локалізація функції зводиться до понять гладкості та кількості зникаючих моментів. Вейвлет-перетворення звичайно поділяють на дискретне вейвлет-перетворення (DWT) та неперервне вейвлет-перетворення (CWT).

Дискретне вейвлет-перетворення (DWT) звичайно використовується для кодування сигналів, у той час як CWT для аналізу сигналів. Саме тому, DWT широко застосовується в інженерній справі і комп'ютерних науках, а CWT у наукових дослідженнях фізичних процесів. Вейвлет-перетворення в наш час^[коли?] взяті на озброєння для величезної кількості різнопланових застосувань, нерідко заміняючи звичайне перетворення Фур'є у багатьох прикладних задачах. Ця зміна парадигми спостерігається в багатьох галузях фізики, включаючи молекулярну динаміку, астрофізику, квантовій механіці, геофізиці, оптиці, механіці рідини та у багатьох інших областях, включаючи обробку зображень, аналізу кров'яного тиску, пульсу та ЕКГ, аналіз ДНК, дослідження білків, вивчення клімату, загальну обробку сигналів, розпізнавання мови, комп'ютерну графіку і мультифрактальний аналіз. Таке широке використання вейвлет-перетворень забезпечується можливістю побудувати на їх основі методи, що потребуватимуть O(N) операцій, на противагу методів Фур'є-перетворень, де кількість операцій не менша за O(NlogN).

Історія

До розроблення вейвлетів призвели декілька незалежних шляхів міркувань, що почалися з робіт Хаара, який на початку двадцятого століття поставив запитання:

«Чи існує інша ортонормальна система ${\displaystyle h_{0}(x),h_{1}(x),...,h_{n}(x),...}$ функцій, визначених на проміжку [0, 1], таких, що довільну функцію ${\displaystyle f(x)\in C[0,1]}$ можна розвинути у суму вигляду ${\displaystyle <f,h_{0}>h_{0}(x)+...+<f,h_{n}>h_{n}(x)+...}$, і що вона буде збіжною до ${\displaystyle f(x)}$ єдиним чином на [0, 1]?»

Як виявилося таких систем можна побудувати нескінченну кількість.

• У 1909 році Хаар запропонував найпростіший розв'язок і тим самим поклав початок до теорії вейвлетів.
• З 1955 Важливий внесок в теорію принесли такі вчені як Морле, Гроссман які сформулювали те що зараз відоме як неперервне вейвлет-перетворення (CWT).
• 1983 Жан Олаф-Штромберґ (Stromberg) та Мейєру (Yves Meyer) визначили та працювали над дискретними вейвлетами.
• 1988 Інгрід Добеші розробила родину функцій на компактному носії.
• 1985-89 Стефан Маллат (Stephane Georges Mallat), спеціаліст з обробки зображень, узагальнив вже існуючі теоретичні розробки: а) квадратурний дзеркальний фільтр (quadrature mirror filter) для цифрової телефонії; б) пірамідальний алгоритм Бурта-Аделсона (Burt Adelson), який використовувався для обробки зображень та в) ортонормальний вейвлет базис Штромберґа та Мейера. Маллат розробив багаторозкладний аналіз (multiresolution analysis).
• 1991 Наталі Делпрат (Nathalie Delprat) надала часово-частотну інтерпретацію CWT (1991)
• 1991 Девід Ньюланд розробив гармонійне вейвлет-перетворення та багато інших.

Приклади, види базисів

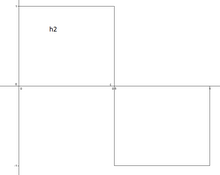
Найпростіша родина вейвлетів, що демонструє основні властивості, такі як ділляція (масштабування), трансляція(зсув), та затухання за межами інтервалу (взагалі компактність носія за визначенням) є система функцій Хаара.

Система будується починаючи з базисної функції ${\displaystyle h(x)=1}$ на [0,1/2) та −1 на [1/2,1), і 0 всюди крім [0, 1). Для ${\displaystyle n\geq 1}$ запишемо ${\displaystyle n=2^{j}+k,j\geq 0,0\leq k<2^{j}}$, і визначимо ${\displaystyle h_{n}(x)=2^{j/2}h(2^{j}-k)}$. Носієм ${\displaystyle h_{n}(x)}$ буде інтервал ${\displaystyle I_{n}=[k2^{-j},(k+1)2^{-j}]}$, що входить до [0, 1), коли ${\displaystyle 0\leq k\leq 2^{j}}$. Для завершення довизначимо ${\displaystyle h_{0}(x)=1}$ на [0, 1). Тепер побудований ряд ${\displaystyle h_{0}(x),h_{1}(x),...,h_{n}(x),...}$ це ортонормальний базис (іноді кажуть Гільбертів базис) в ${\displaystyle L_{2}[0,1]}$. Апроксимація функції ${\displaystyle f(x)}$ послідовністю ${\displaystyle S_{n}(f)(x)=<f,h_{0}>h_{0}(x)+...+<f,h_{n}>h_{n}(x)}$ — це класична апроксимація неперервної функції.

Базисна функція

Ортогональна функція

Ділляція (стистення) ортогональної функція

Трансляція (зсув) ортогональної функція

Можна виділити дві основні операції над вихідною функцією:

• трансляція (зсув) — ${\displaystyle W(2x)\rightarrow W(2x-1)}$
• диляція (стискання, масштабування) ${\displaystyle W(x)\rightarrow W(2x)}$.

На шляху до сучасних побудов теорії хвильок варто відзначити роботи радянського математика Лузіна (30-ті роки), які були продовжені Гвідо Вейссом (Guido Weiss) та Роналдом Куафманом (Ronald R. Coifman) у 60-ті — 80-ті. Їхній підхід використовувався для обробки сиґналів, і оснований на атомарних функціях. Сьогодні цей напрям розвивають учні В. Л. Рвачева (Харків).

Вчені визначили вейвлет як набір функцій, породжених однією «материнською» функцією ${\displaystyle \psi (x)}$. ${\displaystyle \psi _{(a,b)}(x)=a^{-{\frac {n}{2}}}\psi ({\frac {x-b}{a}}),a>0,b\in R^{n}}$. Для функції ${\displaystyle f(x)}$ ці хвилькі ${\displaystyle \psi _{(a,b)}}$ відіграють роль ортонормованого базису, хвилькові коефіцієнти визначаються як ${\displaystyle W(a,b)=<f,\psi _{(a,b))}>}$. Гроссманн та Морле дали наступне визначення: вейвлет це функція ${\displaystyle \psi \in L_{2}(R^{n})}$, претворення Фур'є якої ${\displaystyle {\bar {\psi }}(x)}$ задовольняє умові${\displaystyle \int _{0}^{\infty }|{\bar {\psi }}(t\rho )|^{2}{\frac {dt}{t}}=1,\rho \in R^{n}}$ майже всюди.

За ними вейвлет — це функція ${\displaystyle \psi \in L_{2}(R^{n})}$, така, що ${\displaystyle 2^{\frac {j}{2}}\psi (2^{j}x-k),j,k\in Z}$ утворює ортонормальний базис у ${\displaystyle L_{2}}$.

Найголовніший крок належить Інгрід Добеші (Ingrid Daubechies). У 1988 році вийшла її стаття, де вперше розглядається сімейство ортонормованих систем в ${\displaystyle L_{2}}$ з важливими особливостями:

1. кожна система породжується масштабною функцією ${\displaystyle \phi (x)}$ за допомогою трансляції та диляції;
2. кожен елемент даної системи має компактний носій і неперервний, або може бути вибраний досить гладкий (до певного порядку) шляхом зміни масштабу. Носії базисних функцій стають тим менші чим більший індекс j;
3. існують швидкі алгоритми для обчислень коефіцієнтів розкладу певної функції. Називається — дискретне вейвлет-перетворення від функції до вейвлет коефіцієнтів розкладу. Цей алгоритм має складність порядку O(N);
4. Класичне дискретне перетворення Фур'є та косинус перетворення з'являються як частинний випадок дискретного вейвлет-перетворення (DWT)
5. дискретне вейвлет-перетворення може бути розпаралелене.

Хвильки Добеші

Масштабна функція і відповідна хвилькова функція задовольняють

1. масштабному рівнянню (scaling equation) ${\displaystyle \phi (x):=\sum _{k=0}^{2g-1}a_{k}\phi (2x-k)}$;
2. відповідному хвильковому рівнянню (wavelet equation) ${\displaystyle \psi (x):=\sum _{k=0}^{2g-1}b_{k}\phi (2x-k)}$ ,

де коефіцієнти масштабного рівняння ${\displaystyle a_{k}}$ повинні задовольняти лінійній та квадратичній умовам ${\displaystyle \sum a_{k}=2,\sum a_{k}a_{k+2l}=2\delta (l,0)}$, і де ${\displaystyle b_{k}:=(-1)^{k+1}a_{2g-1-k}}$. Функції ${\displaystyle \phi }$ та ${\displaystyle \psi }$ задані на інтервалі [0, 2g-1] і утворюють трансляцією та диляцією вейвлет систему. Однією з властивостей технонології хвильок (вейвлет) є можливість вибрати систему коефіцієнтів, найбільш адаптовану до даної проблеми. Добеші у своїй роботі визначила сімейство хвилькових (вейвлет) систем, які мають максимальну кількість зникаючих моментів ${\displaystyle \int x^{l}\psi (x)dx=0,l=0,...,g-1}$. Так коли ${\displaystyle g=2}$ можна явно знайти коефіцієнти ${\displaystyle \{a_{n}\}_{n={\bar {o,3}}}}$: ${\displaystyle \{{\frac {1+{\sqrt {3}}}{4}},{\frac {3+{\sqrt {3}}}{4}},{\frac {3-{\sqrt {3}}}{4}},{\frac {1-{\sqrt {3}}}{4}}\}}$. Задавати вейвлет систему можна різним чином. Поширення набуло таке задання ${\displaystyle \phi _{k}(x):=\phi (x-k)}$, ${\displaystyle \psi _{jk}(x):=2^{\frac {j}{2}}\psi (2^{j}x-k),j\geq 0}$. (Зазвичай система об'єднана з масштабними коефіцієнтами.) Вейвлет розвинення: ${\displaystyle f(x)=\sum _{k}f_{k}\phi _{k}(x)+\sum _{j,k}f_{jk}\psi _{jk}(x)}$, де ${\displaystyle f_{k}=\int f(x)\phi _{k}(x)dx}$, ${\displaystyle f_{jk}=\int f(x)\psi _{jk}(x)dx}$.

Приклади базисів

• вейвлет Хаара
• вейвлет Добеши
• вейвлет Гаусса
• вейвлет Мейера (Meyer wavelet)
• вейвлет Морле (Morlet wavelet)
• вейвлет Матьє
• вейвлет Пауля
• вейвлет Ріклера (Ricker wavelet, MHat від англ. Мексиканський капелюх))
• вейвлет Койфмана (Ronald Coifman) — койфлет
• вейвлет Шеннона

Зв'язки теорії вейвлетів

Теорія вейвлетів зв'язана з декількома іншими напрямами. Усі вейвлет-перетворення можуть розглядатися як різновид часово-частотного представлення і, отже відноситься до предмета гармонійного аналізу. Дискретне вейвлет-перетворення може розглядатися як різновид фільтра скінченної імпульсної відповіді. Вейвлети, що утворюють CWT підкоряються принципу невизначеності Гейзенберга і відповідно базис дискретного вейвлета також може розглядатися в контексті інших форм принципу невизначеності.

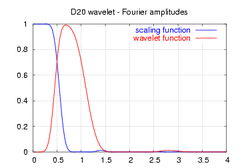
скейлінг-функції ${\displaystyle \phi }$ і вейвлет ${\displaystyle \psi }$
амплітуда частотного спектру

Див. також

• Простір масштабів

Література

• Капшій О. В., Коваль О. І., Русин Б. П. Вейвлет-перетворення у компресії та попередній обробці зображень. — Львів : Сполом, 2008. — 206 с.
• Блаттер К. Вейвлет-анализ. Основы теории. — М. : Техносфера, 2006. — 280 с.
• Добеши И. Десять лекций по вейвлетам. — Ижевск : РХД, 2001. — 464 с.
• Малла С. Вэйвлеты в обработке сигналов. — М. : Мир, 2005. — 672 с.
• Смоленцев Н. К. Введение в теорию вейвлетов. — Ижевск : РХД, 2010. — 292 с.
• Чуи К. Введение в вэйвлеты. — М. : Мир, 2001. — 412 с.

Посилання

• Wavelet Digest [Архівовано 29 вересня 2020 у Wayback Machine.]
• The Wavelet Tutorial by Polikar
• [http://www.autex.spb.ru/cgi-bin/download.cgi?wvlt_tutorial%5Bнедоступне+посилання+з+березня+2019%5D Роби Поликар Введение в Вейвлет-преообразование]^{[недоступне посилання з жовтня 2019]} — 59 с. — Для тих, хто добре зрозумів ДПФ
• J. Lewalle — Введение в анализ данных с применением непрерывного вейвлет-преобразования [Архівовано 22 жовтня 2014 у Wayback Machine.] — 29 с. — Для тих, хто добре зрозумів роботу Робі Поликара «Введение в Вейвлет-преообразование»

1. Ricker, Norman (1953). Wavelet Contraction, Wavelet Expansion, and the Control of Seismic Resolution. Geophysics. 18 (4): 769—792. Bibcode:1953Geop...18..769R. doi:10.1190/1.1437927.