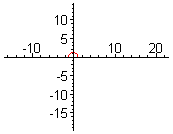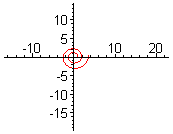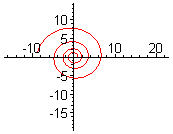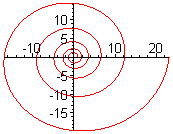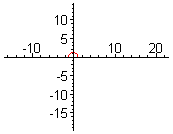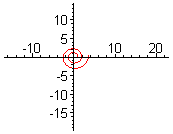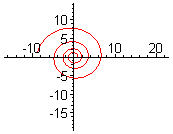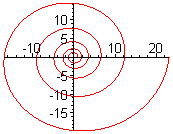Спіраль

Спіра́ль — крива, що обертається навколо деякої точки, поступово наближаючись або віддаляючись від неї, залежно від того, в якому напрямі рухатись вздовж кривої. До найвідоміших спіралей належить спіраль Архімеда, логарифмічна спіраль, евольвента кола та літуус. Подібно до просторового аналогу, гвинтової лінії, спіралі є асиметричні і кожна з них має дві форми, що є відображенням одна одної.

Розріз раковини молюска. Камери мають вигляд подібний до логарифмічної спіралі.

У Вікіпедії є статті про інші значення цього терміна: Спіраль (значення).

Спіраль
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Спіраль у Вікісховищі

Джерела інформації

• David Darling (2004). The Universal Book of Mathematics, from Abracadabra to Zeno's paradoxes. John Wiley & Sons, Inc. ISBN 0-471-27047-4.

Див. також

• Портал «Математика»

• SpiralZoom.com [Архівовано 13 січня 2020 у Wayback Machine.], освітній вебсайт про дослідження механізмів утворення шаблонів, спіралей в природі та спіралі в міфології.

Список літератури

• Cook, T., 1903. Spirals in nature and art. Nature 68 (1761), 296.
• Cook, T., 1979. The curves of life. Dover, New York.
• Habib, Z., Sakai, M., 2005. Spiral transition curves and their applications. Scientiae Mathematicae Japonicae 61 (2), 195 – 206.
• Dimulyo, S., Habib, Z., Sakai, M., 2009. Fair cubic transition between two circles with one circle inside or tangent to the other. Numerical Algorithms 51, 461–476 ^{[недоступне посилання]}.
• Harary, G., Tal, A., 2011. The natural 3D spiral. Computer Graphics Forum 30 (2), 237 – 246 [Архівовано 22 листопада 2015 у Wayback Machine.].
• Xu, L., Mould, D., 2009. Magnetic curves: curvature-controlled aesthetic curves using magnetic fields. In: Deussen, O., Hall, P. (Eds.), Computational Aesthetics in Graphics, Visualization, and Imaging. The Eurographics Association [Архівовано 3 березня 2016 у Wayback Machine.].
• Wang, Y., Zhao, B., Zhang, L., Xu, J., Wang, K., Wang, S., 2004. Designing fair curves using monotone curvature pieces. Computer Aided Geometric Design 21 (5), 515–527 [Архівовано 24 вересня 2015 у Wayback Machine.].
• A. Kurnosenko. Applying inversion to construct planar, rational spirals that satisfy two-point G2 Hermite data. Computer Aided Geometric Design, 27(3), 262-280, 2010 [Архівовано 24 вересня 2015 у Wayback Machine.].
• A. Kurnosenko. Two-point G2 Hermite interpolation with spirals by inversion of hyperbola. Computer Aided Geometric Design, 27(6), 474-481, 2010.
• Miura, K.T., 2006. A general equation of aesthetic curves and its self-affinity. Computer-Aided Design and Applications 3 (1–4), 457–464 [Архівовано 28 червня 2013 у Wayback Machine.].
• Miura, K., Sone, J., Yamashita, A., Kaneko, T., 2005. Derivation of a general formula of aesthetic curves. In: 8th International Conference on Humans and Computers (HC2005). Aizu-Wakamutsu, Japan, pp. 166 – 171 [Архівовано 28 червня 2013 у Wayback Machine.].
• Meek, D., Walton, D., 1989. The use of Cornu spirals in drawing planar curves of controlled curvature. Journal of Computational and Applied Mathematics 25 (1), 69–78 [Архівовано 24 вересня 2015 у Wayback Machine.].
• Farin, G., 2006. Class A Bézier curves. Computer Aided Geometric Design 23 (7), 573–581 [Архівовано 24 вересня 2015 у Wayback Machine.].
• Farouki, R.T., 1997. Pythagorean-hodograph quintic transition curves of monotone curvature. Computer-Aided Design 29 (9), 601–606.
• Yoshida, N., Saito, T., 2006. Interactive aesthetic curve segments. The Visual Computer 22 (9), 896–905 [Архівовано 4 березня 2016 у Wayback Machine.].
• Yoshida, N., Saito, T., 2007. Quasi-aesthetic curves in rational cubic Bézier forms. Computer-Aided Design and Applications 4 (9–10), 477–486 [Архівовано 3 березня 2016 у Wayback Machine.].
• Ziatdinov, R., Yoshida, N., Kim, T., 2012. Analytic parametric equations of log-aesthetic curves in terms of incomplete gamma functions. Computer Aided Geometric Design 29 (2), 129 – 140 [Архівовано 24 вересня 2015 у Wayback Machine.].
• Ziatdinov, R., Yoshida, N., Kim, T., 2012. Fitting G2 multispiral transition curve joining two straight lines, Computer-Aided Design 44(6), 591–596 [Архівовано 24 вересня 2015 у Wayback Machine.].
• Ziatdinov, R., 2012. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function. Computer Aided Geometric Design 29(7): 510-518 [Архівовано 24 вересня 2015 у Wayback Machine.].
• Ziatdinov, R., Miura K.T., 2012. On the Variety of Planar Spirals and Their Applications in Computer Aided Design. European Researcher 27(8-2), 1227-1232 [Архівовано 23 липня 2020 у Wayback Machine.].

Посилання

• Спіраля // Українська мала енциклопедія : 16 кн. : у 8 т. / проф. Є. Онацький. — Накладом Адміністратури УАПЦ в Аргентині. — Буенос-Айрес, 1965. — Т. 7, кн. XIV : Літери Сен — Сті. — С. 1823. — 1000 екз.