Метод Гюккеля

Метод Гю́ккеля або молекулярна орбітальна теорія Гюккеля (англ. Hückel molecular orbital theory) — різновид методу МО ЛКАО для визначення енергій π-орбіталей у делокалізованих π-системах (напр. етилен, бензен, бутадієн).^[1][2] Метод був уперше запропонований Еріхом Гюккелем у 1930 р. як теоретична основа для правила Гюккеля, а пізніше був розширений для гетероциклічних сполук, таких як піридин, пірол або фуран.^[3] Подальше розширення методу Гюккеля, відоме як розширений метод Гюккеля (англ. extended Hückel method, EHM), також бере до уваги σ-електрони. Цей метод був розроблений Роалдом Гоффманом як теоретичний апарат для правил Вудварда–Гоффмана.^[4] Щоб запобігти плутанині, класичний метод Гюккеля тепер також називають простим методом Гюккеля (англ. simple Hückel method, SHM).

Незважаючи на свою відносну математичну простоту й обмеженість молекул, до яких він може бути застосований, метод Гюккеля у своєму первісному вигляді є доволі потужним інструментом для аналізу властивостей кон'югованих π-систем. Опис методу Гюккеля можна зустріти в багатьох вступних підручниках з квантової хімії та фізичної органічної хімії; в органічній хімії ця теорія й досі активно застосовується для передбачення результату реакцій, де беруть участь кон'юговані π-зв'язки (наприклад, перициклічних реакцій).

Математична основа методу

Метод Гюккеля використовує роздільність σ-π-електронів: увага приділяється лише π-МО, оскільки саме вони визначають значну частину хімічних і спектральних властивостей молекул. Конструювання π-МО відбувається тільки з ${\displaystyle 2p_{z}}$-орбіталей, які ортогональні до атомних орбіталей, що утворюють σ-зв'язки, тобто каркас молекули. Наступне припущення полягає в тому, що тільки суміжні ${\displaystyle 2p_{z}}$-орбіталі задіяні в кон'югації; тобто, подвійні зв'язки, які розділені щонайменш одним атомом, що утворює лише насичені зв'язки, розглядаються як дві окремі π-МО.

Для кон'югованих лінійних полієнів (наприклад, 1,3,5-гексатрієн), енергетичні рівні π-МО задані рівнянням:

${\displaystyle E_{j}=\alpha +m_{j}\beta }$,

де

${\displaystyle m_{j}=2cos(j\pi /n+1)}$,

${\displaystyle j=1,2,3,...,n}$,

із числом атомів Карбону ${\displaystyle n}$ в ланцюзі.^[5]

Величина ${\displaystyle \alpha }$ — Кулонівський інтеграл. Він відображає енергію зв'язаного електрону в ${\displaystyle 2p_{z}}$-орбіталі та вважається постійним для всіх ${\displaystyle sp^{2}}$-гібридизованих атомів Карбону. Величина ${\displaystyle \beta }$ — резонансний інтеграл; вона визначає зміну в енергії електрона, делокалізованого між декількома ${\displaystyle 2p_{z}}$-орбіталями. Значення величин ${\displaystyle \alpha }$ і ${\displaystyle \beta }$ вираховують за методом Гартрі–Фока.

Для повністю делокалізованих циклічних полієнів застосовується формула:

${\displaystyle m_{j}=2cos(2j\pi /n+1)}$,

${\displaystyle j=\pm 1,\pm 2,\pm 3,...,(n-1)/2}$ для парного числа атомів Карбону й ${\displaystyle (n/2)}$ для непарного.

Лінійні полієни

Знаючи енергії орбіталей, можна сконструювати діаграму МО; ті орбіталі, для яких ${\displaystyle m_{j}>0}$ є зв'язуючими, а орбіталі з ${\displaystyle m_{j}<0}$ є розрихлюючими. Кожна орбіталь має певну кількість вузлових площин: для орбіталі з енергією ${\displaystyle E_{j}}$ кількість вузлових площин дорівнює ${\displaystyle (j-1)}$. Вузлові площини завжди проходять через найбільш симетричні точки в МО.

Нижче наведені діаграми МО для етилену, бутадієну й гексатрієну (червоним позначені вузлові площини):^[6]

Для π-систем з непарною кількістю атомів Карбону діє такий же принцип, але кількість МО в такому випадку теж буде непарною, а одна орбіталь буде незв'язуючою:^[6]

Циклічні полієни: Цикл Фроста

Докладніше: Цикл Фроста

Вид діаграм МО для спряжених циклічних полієнів лежить в основі так званого циклу Фроста-Музуліна (зазвичай використовують назву "цикл Фроста"). Розрахунок енергій МО, як це описано вище, приводить до цікавого спостереження, що циклічні полієни з ${\displaystyle n}$ атомів Карбону, які мають головну вісь обертання C_n, мають такі енергії МО, що їх можна розмістити у вершинах звичайного ${\displaystyle n}$-кутника.^[7] Молекули, які мають непарну кількість електронних пар (${\displaystyle 4n+2}$ π-електронів), повністю заповнюють зв'язуючі й незв'язуючі орбіталі, що є енергетично вигідним. Тому такі сполуки відносяться до ароматичних. При парній кількості електронних пар (${\displaystyle 4n}$ π-електронів) заповнення МО утворює дирадикал, що робить молекулу дуже реактивною, а також є енергетично невигідним. Такі сполуки нестійкі й відносяться до антиароматичних.

• Приклади ароматичних сполук
• 
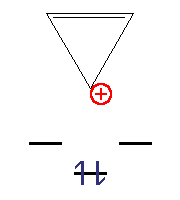
  Циклопропеніл-катіон
• 
  Циклопентадієніл-аніон
• 
  Циклогептатрієніл-катіон (тропілій-катіон)

• Приклади антиароматичних сполук
• 
  Циклобутадієн
• 
  Циклопентадієніл-катіон
• 
  Циклогептатрієніл-аніон

Див. також

• Ароматичність
• Правила Вудворда–Гоффмана
• Перициклічна реакція
• Метод Гартрі–Фока

Примітки

1. E. Hückel, Zeitschrift für Physik, 70, 204 (1931); 72, 310 (1931); 76, 628 (1932); 83, 632 (1933).
2. Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.
3. Andrew Streitwieser, Molecular Orbital Theory for Organic Chemists, Wiley, New York (1961).
4. "Stereochemistry of Electrocyclic Reactions", R. B. Woodward, Roald Hoffmann, J. Am. Chem. Soc., 1965; 87(2); 395–397. DOI:10.1021/ja01080a054.
5. Carey, Francis A. (2013). Advanced Organic Chemistry : Part a: Structure and Mechanisms. Springer. ISBN 978-1-4613-9795-3. OCLC 1059416763.
6. Sankararaman, S. (Sethuraman), 1957- (2005). Pericyclic reactions : a textbook : reactions, applications, and theory. Weinheim: Wiley-VCH. ISBN 3-527-31439-3. OCLC 61439936.
7. Frost, Arthur A.; Musulin, Boris (1953-03). A Mnemonic Device for Molecular Orbital Energies. The Journal of Chemical Physics. Т. 21, № 3. с. 572—573. doi:10.1063/1.1698970. ISSN 0021-9606. Процитовано 2 лютого 2020.