Дельтаедри

Дельтаэдр — це багатогранник, всі грані якого є правильними трикутниками. Назву взято від грецької великої літери дельта (${\displaystyle \Delta }$), яка має форму рівностороннього трикутника. Існує нескінченно багато дельтаедрів, але з них лише вісім опуклі, і вони мають 4, 6, 8, 10, 12, 14, 16 і 20 граней^[1].

Найбільший строго опуклий дельтаедр є правильним ікосаедром

Зрізаний тетраедр з шестикутниками, розбитими на трикутники. Це тіло не є строго опуклим дельтаедром, оскільки розташовані в одній площині грані неприпустимі за визначенням.

Нижче перелічено числа граней, ребер і вершин для кожного з восьми дельтаедрів.

Опуклі дельтаедри

Всього існує 8 опуклих дельтаедрів^[2], 3 з яких є платоновими тілами, а 5 — багатогранниками Джонсона.

У дельтаедра з 6 гранями деякі вершини мають ступінь 3, а деякі — ступінь 4. У дельтаедрів з 10, 12, 14 і 16 гранями деякі вершини мають ступінь 4, а деякі — ступінь 5. Ці п'ять неправильних дельтаедрів належать до класу правильногранних багатогранників — опуклих багатогранників з гранями у вигляді правильних багатокутників.

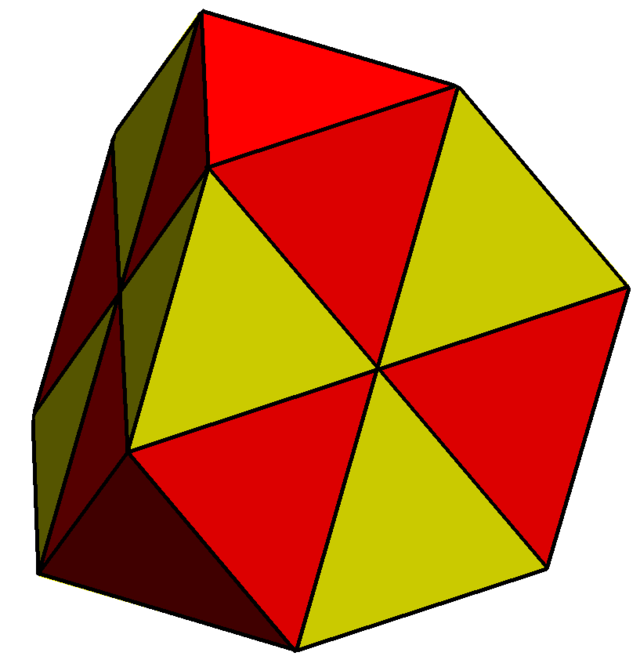
Не існує опуклого дельтаедра з 18 гранями^[3]. Однак ікосаедр зі стягнутим ребром^[en] є прикладом октаедра, який можна зробити опуклим з 18 неправильними гранями, або з двома наборами по три рівносторонніх трикутники, що лежать в одній площині.

Правильні дельтаедри
Назва	Зображення	Кількість вершин	Кількість ребер	Кількість граней	Конфігурація вершини	Група симетрії
Правильний тетраедр		4	6	4	4 × 33	Td, [3,3]
Правильний октаедр (чотирикутна біпіраміда)		6	12	8	6 × 34	Oh, [4,3]
Правильний ікосаедр		12	30	20	12 × 35	Ih, [5,3]
Дельтаедри Джонсона
Трикутна біпіраміда		5	9	6	2 × 33 3 × 34	D3h, [3,2]
П'ятикутна біпіраміда		7	15	10	5 × 34 2 × 35	D5h, [5,2]
Кирпатий двоклиноїд		8	18	12	4 × 34 4 × 35	D2d, [2,2]
Тричі нарощена трикутна призма		9	21	14	3 × 34 6 × 35	D3h, [3,2]
Скручено-подовжена чотирикутна біпіраміда		10	24	16	2 × 34 8 × 35	D4d, [4,2]

Нестрого опуклі випадки

Існує нескінченно багато дельтаедрів з копланарними (належними одній площині) трикутниками. Якщо множини копланарних трикутників вважати однією гранню, можна нарахувати менше граней, ребер і вершин. Копланарні трикутні грані можуть бути злиті в ромбічні, трапецієподібні, шестикутні або інші рівносторонні багатокутні грані. Кожна грань має бути опуклим поліамондом, таким як , , , , , , і , …^[4]

Деякі невеликі приклади

оКопланарные дельтаэдры

Малюнок	Назва	Граней	Ребер	Вершин	Конфігурації вершин	Група симетрії
	Нарощений октаедр[en] Нарощення 1 тетр. + 1 окт.	10	15	7	1 × 33 3 × 34 3 × 35 0 × 36	C3v, [3]
		4 3	12
	Трикутний трапецоедр[en] Нарощення 2 тетр. + 1 окт.	12	18	8	2 × 33 0 × 34 6 × 35 0 × 36	C3v, [3]
		6	12
	Нарощення 2 тетр. + 1 окт.	12	18	8	2 × 33 1 × 34 4 × 35 1 × 36	C2v, [2]
		2 2 2	11	7
	Трикутна зрізана піраміда Нарощення 3 тетр. + 1 окт.	14	21	9	3 × 33 0 × 34 3 × 35 3 × 36	C3v, [3]
		1 3 1	9	6
	Подовжений октаедр(інші мови) Нарощення 2 тетр. + 2 окт.	16	24	10	0 × 33 4 × 34 4 × 35 2 × 36	D2h, [2,2]
		4 4	12	6
	Тетраедр Нарощення 4 тетр. + 1 окт.	16	24	10	4 × 33 0 × 34 0 × 35 6 × 36	Td, [3,3]
		4	6	4
	Нарощення 3 тетр. + 2 окт.	18	27	11	1 × 33 2 × 34 5 × 35 3 × 36	D2h, [2,2]
		2 1 2 2	14	9
	Ікосаедр зі стягнутим ребром[en]	18	27	11	0 × 33 2 × 34 8 × 35 1 × 36	C2v, [2]
		12 2	22	10
	Двозрізана біпіраміда[en] Нарощення 6 тетр. + 2 окт.	20	30	12	0 × 33 3 × 34 6 × 35 3 × 36	D3h, [3,2]
		2 6	15	9
	Трискатний купол Нарощення 4 тетр. + 3 окт.	22	33	13	0 × 33 3 × 34 6 × 35 4 × 36	C3v, [3]
		3 3 1 1	15	9
	Трикутна біпіраміда Нарощення 8 тетр. + 2 окт.	24	36	14	2 × 33 3 × 34 0 × 35 9 × 36	D3h, [3]
		6	9	5
	Шестикутна антипризма	24	36	14	0 × 33 0 × 34 12 × 35 2 × 36	D6d, [12,2+]
		12 2	24	12
	Зрізаний тетраедр Нарощення 6 тетр. + 4 окт.	28	42	16	0 × 33 0 × 34 12 × 35 4 × 36	Td, [3,3]
		4 4	18	12
	Тетракіскубоктаедр[en]Октаедр Нарощення 8 тетр. + 6 окт.	32	24	18	0 × 33 12 × 34 0 × 35 6 × 36	Oh, [4,3]
		8	12	6

Неопуклі дельтаедри

Неопуклих і тороїдальних дельтаедрів існує нескінченно багато.

Приклад дельтаедра з самоперетинами граней:

• Великий ікосаедр — тіло Кеплера — Пуансо, з 20 трикутниками, що перетинаються

  

Інші неопуклі дельтаедри можна отримати шляхом додавання пірамід до граней всіх 5 правильних багатогранників:

Триакістетраедр	Тетракісгексаедр	Триакісоктаедр (stella octangula)	Пентакісдодекаедр	Триакісікосаедр
12 трикутників	24 трикутників		60 трикутників

Інші нарощення тетраедрів:

Приклади: Нарощені тетраедри

8 трикутників	10 трикутників	12 трикутників

Також шляхом додавання до граней перекинутих пірамід:

Виїмчастий додекаедр[en]	Тороїдальний дельтаедр
60 трикутників	48 трикутників