Верхня і нижня границі

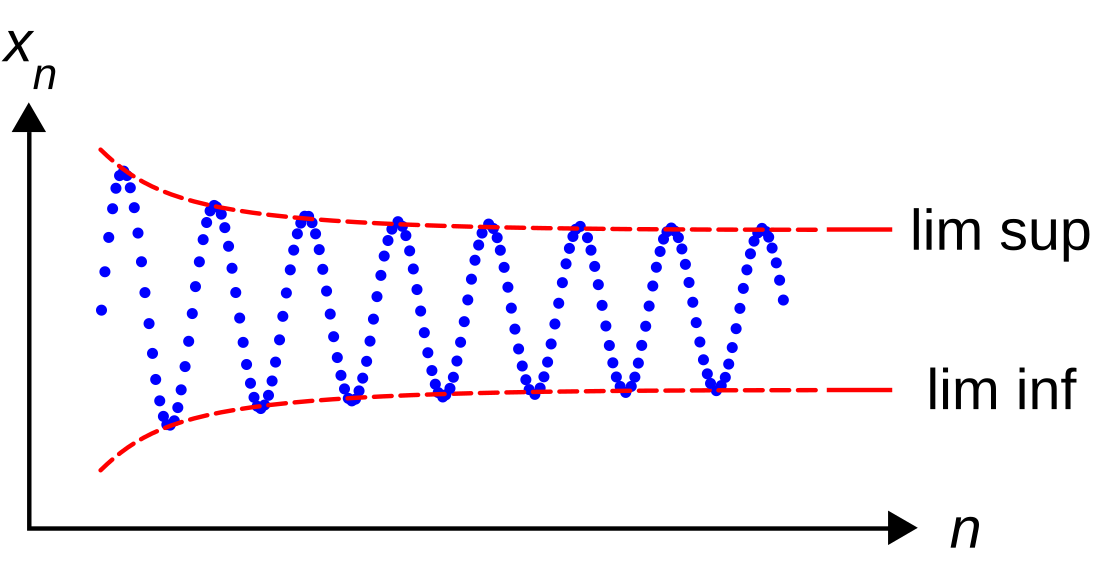
В математичному аналізі верхня і нижня границі визначаються для числових послідовностей чи функцій і використовуються при їх вивченні. На відміну від звичайної границі, верхня і нижня границі завжди існують (хоч і можуть бути рівними нескінченності). Для нижньої границі послідовності ${\displaystyle \left\{x_{n}\right\}_{n=1}^{\infty }}$ використовуються позначення ${\displaystyle \varliminf _{n\to \infty }x_{n}}$ (поширене в українській і російській літературі) і ${\displaystyle \liminf _{n\to \infty }x_{n}}$ (поширеніше в західній літературі). Для верхньої границі відповідні позначення мають вигляд ${\displaystyle \varlimsup _{n\to \infty }x_{n}}$ і ${\displaystyle \limsup _{n\to \infty }x_{n}.}$

Верхня границя (limsup) і нижня границя (liminf)

Визначення

Визначення для послідовностей

Нижню границю послідовності можна визначити:

${\displaystyle \varliminf _{n\to \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\inf _{m\geq n}x_{m}{\Big )}}$

або

${\displaystyle \varliminf _{n\to \infty }x_{n}:=\sup _{n\geq 0}\,\inf _{m\geq n}x_{m}=\sup\{\,\inf\{\,x_{m}:m\geq n\,\}:n\geq 0\,\}.}$

Подібним чином верхня границя послідовності (x_n) визначається

${\displaystyle \limsup _{n\to \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\sup _{m\geq n}x_{m}{\Big )}}$

або

${\displaystyle \limsup _{n\to \infty }x_{n}:=\inf _{n\geq 0}\,\sup _{m\geq n}x_{m}=\inf\{\,\sup\{\,x_{m}:m\geq n\,\}:n\geq 0\,\}.}$

Визначення для функцій

Нехай дано дійсну функцію ${\displaystyle f:I\to \mathbb {R} ,}$ де ${\displaystyle I\subset \mathbb {R} ,}$ і ξ — граничну точку I, тоді верхню і нижню границю функції в точці ξ можна визначити:

${\displaystyle \varlimsup _{x\to \xi }f(x)=\inf _{a>0}\sup f((\xi -a,\xi +a)\cap I),}$

${\displaystyle \varliminf _{x\to \xi }f(x)=\sup _{a>0}\inf f((\xi -a,\xi +a)\cap I).}$

Аналогічно можна визначити односторонні границі функції в точці:

${\displaystyle \varlimsup _{x\to \xi +}f(x)=\inf _{a>0}\sup f((\xi ,\xi +a)\cap I),}$

${\displaystyle \varliminf _{x\to \xi +}f(x)=\sup _{a>0}\inf f((\xi ,\xi +a)\cap I),}$

${\displaystyle \varlimsup _{x\to \xi -}f(x)=\inf _{a>0}\sup f((\xi -a,\xi )\cap I),}$

${\displaystyle \varliminf _{x\to \xi -}f(x)=\sup _{a>0}\inf f((\xi -a,\xi )\cap I).}$

Визначення для послідовності множин

Нехай Ω — деяка множина, (A_n) — послідовність її підмножин. Тоді верхня і нижня границі цієї послідовності визначаються за формулами:

${\displaystyle \varliminf _{n\rightarrow \infty }A_{n}={\bigcup _{n=1}^{\infty }}\left({\bigcap _{m=n}^{\infty }}A_{m}\right)}$

і

${\displaystyle \varlimsup _{n\rightarrow \infty }A_{n}={\bigcap _{n=1}^{\infty }}\left({\bigcup _{m=n}^{\infty }}A_{m}\right).}$

Приклади

• ${\displaystyle \varliminf _{n\to \infty }{\frac {1}{n}}=\varlimsup _{n\to \infty }{\frac {1}{n}}=0}$

• ${\displaystyle \varliminf _{n\to \infty }\left(-1\right)^{n}=-1}$

• ${\displaystyle \varlimsup _{n\to \infty }\left(-1\right)^{n}=+1}$

Властивості

• У будь-якої послідовності існують верхня і нижня границі, що належать множині ${\displaystyle \mathbb {R} \cup \lbrace -\infty ,+\infty \rbrace .}$
• Числова послідовність ${\displaystyle ~\{x_{n}\}}$ збігається до ${\displaystyle ~a}$ тоді і тільки тоді, коли ${\displaystyle \varliminf _{n\rightarrow \infty }x_{n}=\varlimsup _{n\rightarrow \infty }x_{n}=a}$.
• Для будь-якого наперед узятого додатного числа ${\displaystyle ~\varepsilon }$ всі елементи обмеженої числової послідовності ${\displaystyle \left\{x_{n}\right\}_{n=1}^{\infty }}$, починаючи з деякого номера, залежного від ${\displaystyle ~\varepsilon }$, лежать усередині інтервалу ${\displaystyle \left(\varliminf _{n\to \infty }x_{n}-\varepsilon ,\varlimsup _{n\to \infty }x_{n}+\varepsilon \right)}$.
• Якщо за межами інтервалу ${\displaystyle \left(a,b\right)}$ лежить лише скінченна кількість елементів обмеженої числової послідовності ${\displaystyle \left\{x_{n}\right\}_{n=1}^{\infty }}$, то інтервал ${\displaystyle \left(\varliminf _{n\to \infty }x_{n},\varlimsup _{n\to \infty }x_{n}\right)}$ міститься в інтервалі ${\displaystyle \left(a,b\right)}$.
• Виконуються нерівності:
• ${\displaystyle \inf _{n}x_{n}\leq \liminf _{n\to \infty }x_{n}\leq \limsup _{n\to \infty }x_{n}\leq \sup _{n}x_{n}}$
• ${\displaystyle \varlimsup _{n\to \infty }(a_{n}+b_{n})\leq \varlimsup _{n\to \infty }(a_{n})+\varlimsup _{n\to \infty }(b_{n}).}$

${\displaystyle \varliminf _{n\to \infty }(a_{n})+\varliminf _{n\to \infty }(b_{n})\leq \varliminf _{n\to \infty }(a_{n}+b_{n}).}$

Див. також

• Верхня та нижня межа
• Інфімум та супремум

Джерела

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)
• Банах С. Диференціальне та інтегральне числення = Rachunek różniczkowy i całkowy. — 2-е. — М. : Наука, 1966. — 436 с.(рос.)
• Ляшко І.І., Ємельянов В.Ф., Боярчук О.К. Математичний аналіз. Частина 1. — К. : Вища школа, 1992. — 496 с. — ISBN 5-11-003757-4.(укр.)
• Дороговцев А. Я. Математичний аналіз. Частина 1. — К. : Либідь, 1993. — 320 с. — ISBN 5-325-00380-1.(укр.)