Модель Воттса — Строгаца

Модель Воттса-Строгаца — це модель генерації випадкових графів, яка створює графи з властивостями тісного світу, зокрема з короткою середньою довжиною шляху та високою кластеризацією. Модель була запропонована Данканом Дж. Воттсом^[en] та Стівеном Строгацом у їх спільній статті в журналі Nature 1998 року.^[1] Модель також відома як (Watts) бета модель після того, як Воттс використовував ${\displaystyle \beta }$ для опису моделі в своїй популярній науковій книзі Six Degrees^[en].

Обґрунтування для моделі

Формальне вивчення випадкових графів датується роботою Пала Ердеша та Альфреда Реньї^[2]. Графи, які вони розглядали, тепер відомі як класичні графи або модель Ердеша — Реньї, пропонують просту та потужну модель з багатьма додатками.

Проте модель Ердеша — Реньї не має двох важливих властивостей, що спостерігаються в багатьох реальних мережах:

1. Вони не генерують місцеві кластери та тріадичні замикання^[en]. Натомість, оскільки вони мають постійну, випадкову та незалежну ймовірність підключення двох вузлів, модель Ердеша — Реньї має низький коефіцієнт кластеризації.
2. Вони не враховують утворення вузлів. Формально ступінь вершини розподілу графа Ердеша-Реньї сходиться до розподілу Пуассона, а не до закону потужності, що спостерігається в багатьох реальних безмасштабних мережах.^[3]

Модель Ердеша — Реньї була спроектована як найпростіша модель, яка стосується першого з двох обмежень. Це припускає кластеризацію, зберігаючи короткі довжини шляху моделі Ердеша-Реньї. Це відбувається шляхом інтерполяції між ЕР-графіком і регулярною кільцевою решіткою. Отже, модель здатна принаймні частково пояснити «малі світові» явища в різних мережах, таких як енергетична мережа, нейронна мережа C elegans та мережа кіноакторів. У 2015 році дослідники з Каліфорнійського технологічного інституту та Принстонського університету показали, що модель Воттса-Строгаца пояснює зв'язок жирового обміну в дріжджах^[4], що починають жити.

Алгоритм

Watts–Strogatz graph

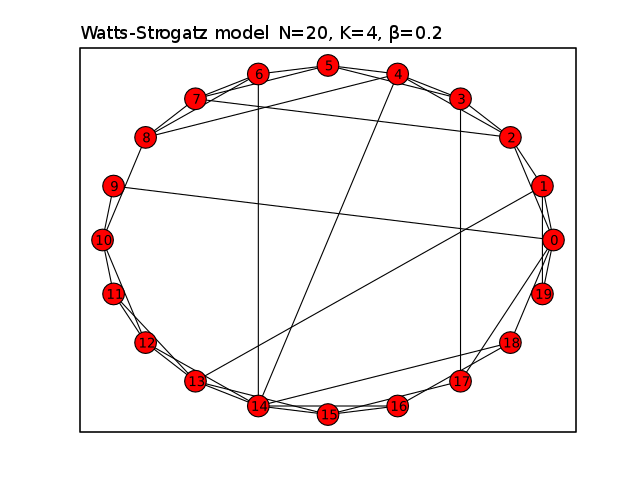
Враховуючи бажану кількість вузлів ${\displaystyle N}$, означає ступінь ${\displaystyle K}$ (вважається рівним цілим числом) і спеціальний параметр ${\displaystyle \beta }$, що задовольняє (${\displaystyle 0\leq \beta \leq 1}$ i ${\displaystyle N\gg K\gg \ln N\gg 1}$. Модель конструює неорієнтований граф з ${\displaystyle N}$-вузлами та ${\displaystyle {\frac {NK}{2}}}$ зв'язками за таким чином:

1. Побудуйте правильну кільцеву решітку, графік з ${\displaystyle N}$ вузлами, кожен з яких з'єднаний з ${\displaystyle K}$ сусідніми, ${\displaystyle K/2}$ з кожного боку. Тобто, якщо вузли позначені ${\displaystyle n_{0}\ldots n_{N-1}}$, є ребро ${\displaystyle (n_{i},n_{j})}$ якщо і тільки якщо ${\displaystyle 0<|i-j|\mod \left(N-1-{\frac {K}{2}}\right)\leq {\frac {K}{2}}.}$
2. Для кожного вузла ${\displaystyle n_{i}=n_{0},\dots ,n_{N-1}}$, ${\displaystyle (n_{i},n_{j})}$ з ${\displaystyle i<j}$, перемотати його з ймовірністю ${\displaystyle \beta }$ бета-версія. Перемотування здійснюється шляхом заміни ${\displaystyle (n_{i},n_{j})}$ з ${\displaystyle (n_{i},n_{k})}$, де ${\displaystyle k}$ вибирається з рівномірною ймовірністю з усіх можливих значень, які уникають самоплетіння (${\displaystyle k\neq i}$) та дублювання посилань (немає краю ${\displaystyle (n_{i},n_{k'})}$ з ${\displaystyle k'=k}$ в цій точці алгоритму).

Властивості

Основна решітка структури моделі створює локально кластеризовану мережу, а випадкові зв'язки різко зменшують середню довжину шляху. Алгоритм представляє ${\displaystyle \beta {\frac {NK}{2}}}$ решітчастих країв. Різні ${\displaystyle \beta }$ дозволяє інтерполювати між регулярною ґраткою (${\displaystyle \beta =0}$) і випадковим графіком (${\displaystyle \beta =1}$) наближаючись до випадкового графа Ердеша-Реньї ${\displaystyle G(n,p)}$ з ${\displaystyle n=N}$ і ${\displaystyle p={\frac {NK}{2{N \choose 2}}}}$.

Три цікаві властивості — це середня довжина шляху, високий коефіцієнт кластеризації та розподіл ступеня.

Середня довжина шляху

Для кільцевої решітки середня довжина шляху становить ${\displaystyle \ell (0)=N/2K\gg 1}$ і масштабується лінійно з розміром системи. У граничному випадку ${\displaystyle \beta \rightarrow 1}$ граф сходиться до класичного випадкового графа з ${\displaystyle \ell (1)={\frac {\ln N}{\ln K}}}$. Проте в проміжній області ${\displaystyle 0<\beta <1}$ середня довжина шляху падає дуже швидко з збільшенням ${\displaystyle \beta }$, швидко наближаючись до його граничного значення.

Коефіцієнт кластеризації

Для кільцевої решітки коефіцієнт кластеризації^[5] ${\displaystyle C(0)={\frac {3(K-2)}{4(K-1)}}}$, і тому має тенденцію до ${\displaystyle 3/4}$, оскільки ${\displaystyle K}$ зростає незалежно від розміру системи.^[6] У граничному випадку ${\displaystyle \beta \rightarrow 1}$ коефіцієнт кластеризації досягає значення для класичних випадкових графів ${\displaystyle C(1)=K/N}$ і, таким чином, обернено пропорційний розміру системи. У проміжному регіоні коефіцієнт кластеризації залишається досить близьким до його значення для звичайної решітки і лише падає при відносно високому (\ displaystyle \ beta) \ beta. Це призводить до регіону, де середня довжина шляху швидко падає, але коефіцієнт кластеризації не пояснюється явищем «малого світу».

Якщо ми використовуємо міру Barrat і Weigt^[6] для кластеризації ${\displaystyle C'(\beta )}$, визначеної як частка між середньою кількістю ребер між сусідами вузла та середньою кількістю можливі краї між цими сусідами або, альтернативно,

${\displaystyle C'(\beta )\equiv {\frac {3\times {\text{number of triangles}}}{\text{number of connected triples}}}}$

то ми отримаємо ${\displaystyle C'(\beta )\sim C(0)(1-\beta )^{3}.}$

Розподіл ступеня

Розподіл ступенів у випадку кільцевої решітки є просто дельта-функцією Дірака, центрованою в ${\displaystyle K}$. У граничному випадку ${\displaystyle \beta \rightarrow 1}$ це розподіл Пуассона, як з класичними графіками. Розподіл ступенів для ${\displaystyle 0<\beta <1}$ можна записати як,^[6]

${\displaystyle P(k)=\sum _{n=0}^{f(k,K)}C_{K/2}^{n}(1-\beta )^{n}\beta ^{K/2-n}{\frac {(\beta K/2)^{k-K/2-n}}{(k-K/2-n)!}}e^{-\beta K/2}}$

де ${\displaystyle k_{i}}$ — це кількість ребер, які мають вузол ${\displaystyle i^{\text{th}}}$ або її ступінь. Тут ${\displaystyle k\geq K/2}$ та ${\displaystyle f(k,K)=\min(k-K/2,K/2)}$. Форма розподілу ступенів аналогічна розподілу ступеня і має яскраво виражений пік при ${\displaystyle k=K}$ і розпадається експоненціально для великих ${\displaystyle |k-K|}$. Топологія мережі є відносно однорідною, і всі вузли більш-менш однакові.

Обмеження

Основним обмеженням моделі є те, що він виробляє нереальний ступінь вершини. На відміну від цього, реальні мережі часто безмаштабні мережі, неоднорідні в ступені, мають концентратори та безмаштабний розподіл ступенів. Такі мережі краще описуються в цьому відношенні переважним сімейством моделей приєднання, такими як модель Барабаші-Альберта (БА). (З іншого боку, модель Барабаші-Альберт не здатна забезпечити високий рівень кластеризації в реальних мережах, це недолік, який не використовується моделями Воттса-Строгаца. Таким чином, ні модель Воттса-Строгаца, ні модель Барабаші-Альберт не можна вважати цілком реалістичними.)

Модель Воттса-Строгаца також передбачає фіксовану кількість вузлів і, таким чином, не може бути використана для моделювання зростання мережі.

Див. також

• Світ тісний (граф)
• Граф Радо
• Модель Ердеша — Реньї
• Модель Барабаші — Альберт
• Соціальна мережа

Посилання

1. Watts, D. J.; Strogatz, S. H. (1998). Collective dynamics of 'small-world' networks (PDF). Nature. 393 (6684): 440—442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998. Архів оригіналу (PDF) за 11 квітня 2020. Процитовано 28 листопада 2017.
2. Erdos, P. (1960). Publications Mathematicae 6, 290 (1959); P. Erdos, A. Renyi. Publ. Math. Inst. Hung. Acad. Sci. 5: 17.
3. Ravasz, E. (30 серпня 2002). Hierarchical Organization of Modularity in Metabolic Networks. Science. 297 (5586): 1551—1555. Bibcode:2002Sci...297.1551R. doi:10.1126/science.1073374.
4. Al-Anzi, Bader; Arpp, Patrick; Gerges, Sherif; Ormerod, Christopher; Olsman, Noah; Zinn, Kai (2015). Experimental and Computational Analysis of a Large Protein Network That Controls Fat Storage Reveals the Design Principles of a Signaling Network. PLOS Computational Biology. 11 (5): e1004264. Bibcode:2015PLSCB..11E4264A. doi:10.1371/journal.pcbi.1004264. PMID 26020510.{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання)
5. Albert, R., Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics. 74 (1): 47—97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
6. Barrat, A.; Weigt, M. (2000). On the properties of small-world network models (PDF). European Physical Journal B. 13 (3): 547—560. doi:10.1007/s100510050067. Процитовано 26 лютого 2008.^{[недоступне посилання]}