From Wikipedia, the free encyclopedia
நொதி இயக்கவியல் (enzyme kinetics) என்பது நொதிகளால் வினையூக்கியாக்கப்படும் வேதி வினைகள் பற்றிய ஒரு ஆய்வாகும். நொதி இயக்கவியலில், வினை விகிதம் அளவிடப்பட்டு வினையின் மாறுபடும் நிலைமைகளின் விளைவுகள் சோதனை செய்யப்படுகிறது. ஒரு நொதியின் இயக்கவியல் இவ்வகையில் ஆய்வு செய்யப்படுவதால் இந்த நொதியின் வினையூக்கும் இயக்கமுறையை, வளர்ச்சிதைமாற்றத்தில் அதன் பங்கு, அதன் செயல்பாடு எவ்வாறு கட்டுப்படுத்தப்படுகிறது மற்றும் ஒரு மருந்து அல்லது நச்சு நொதியை எவ்வாறு தடுத்துநிறுத்துகிறது ஆகியவற்றை வெளிப்படுத்தும்.
 | இந்த கட்டுரைக்கு நிபுணரின் கவனம் தேவைப்படுகிறது. மேலும் விவரங்களுக்கு உரையாடல் பக்கத்தினை பார்க்க. விக்கித்திட்டம் உயிரியல் அல்லது உயிரியல் வலைவாசல் வழியாக ஒரு நிபுணரைத் தேட உதவலாம். |
நொதிகள் பொதுவாக இதர மூலக்கூறுகளைக் (நொதியின் அடி மூலக்கூறுகள்) கையாளக்கூடிய புரத மூலக்கூறுகளாகும். இந்த இலக்கு மூலக்கூறுகள், ஒரு நொதியின் வினைபுரி இடத்துடன் பிணைந்து நொதியின் இயக்கமுறை எனப்படும் தொடர்ச்சியான படிநிலை மூலம் ஆக்கப் பொருட்களாக மாற்றம் செய்யப்படுகின்றன. இந்த இயக்கமுறைகள் ஒற்றை-அடி மூலக்கூறு மற்றும் பன்மடங்கு-அடி மூலக்கூறு இயக்கமுறைகளாக வகுக்கப்படலாம். டிரையோஸ்பாஸ்பேட் ஐசோமிரேஸ் போன்ற ஒரே ஒரு அடி மூலக்கூற்றை மட்டுமே பிணைக்கும் நொதி மீதான இயக்கவியல் ஆய்வுகள், இந்த அடி மூலக்கூற்றைப் பிணைக்கும் இணக்கம் மற்றும் கொள்முதல் விகிதத்தை அளவிடும் நோக்கைக் கொண்டிருக்கிறது.
டைஹைட்ரோஃபோலேட் ரிடக்டேஸ் (வலப்புறம் காட்டப்பட்டுள்ளது) போன்ற பன்மடங்கு அடி மூலக்கூற்றை நொதி பிணைக்கும்போது, இந்த அடி மூலக்கூறுகள் பிணையும் வரிசைமுறை மற்றும் ஆக்கப்பொருட்கள் வெளியிடப்படும் வரிசைமுறையையும் கூட இந்த நொதி இயக்கவியலால் காட்ட முடியும். ஒரு ஒற்றை அடி மூலக்கூற்றைப் பிணைத்துப் பன்மடங்கு ஆக்கப்பொருட்களை வெளியிடும் நொதியின் உதாரணமாக இருப்பது புரத நொதிப்புகள், இவை ஒரு புரத அடி மூலக்கூற்றை இரு பாலிபெப்டைட் ஆக்கப்பொருளாகப் பிளவு படுத்துகிறது. மற்றவை இரு அடி மூலக்கூறுகளை ஒன்றாக இணைக்கின்றன, அதாவது டிஎன்ஏ பலபடியாக்கும் நொதி ஒரு நியூக்ளியோட்டைடுவை டிஎன்ஏவுடன் இணைப்பது போன்றது. இந்த இயக்கமுறைகள் அவ்வப்போது ஒரு கடினமான படிநிலைத் தொடர்ச்சியாக இருந்தபோதிலும், ஒட்டுமொத்த இயக்கவியலைத் தீர்மானிக்கும் ஒரு வழக்கமான விகிதம்-தீர்மானிக்கும்-படிநிலை இருக்கிறது. இந்த விகிதம்-தீர்மானிக்கும்-படிநிலை என்பது ஒரு வேதி வினையாக அல்லது நொதியிலிருந்து வெளிப்படும் ஆக்கப்பொருட்களில் ஈடுபட்டுள்ளவை போன்ற நொதி அல்லது அடி மூலக்கூற்றின் வெளிவடிவ அமைப்புக்குரிய மாற்றமாகவும் இருக்கலாம்.
நொதியின் கட்டமைப்பு பற்றிய அறிவு, இயக்கத் தரவின் பொருள்விளக்கத்தை அறிந்துகொள்வதில் பயனுடையதாக இருக்கும். உதாரணத்திற்கு, வினையூக்கியின்போது அடி மூலக்கூறு மற்றும் ஆக்கப் பொருட்கள் எவ்வாறு பிணைகின்றன, வினைகளின் போது என்னென்ன மாற்றங்கள் நிகழ்கின்றன மற்றும் இயக்கமுறையில் குறிப்பிட்ட அமினோ அமில எச்சங்களின் பங்கினைப் பற்றியும் கூட கட்டமைப்பு ஆலோசனை கூறலாம். இயக்கமுறையின் போது சில நொதிகள் குறிப்பிடும்படியான விகிதத்தில் வடிவ மாற்றம் பெறுகின்றன; அத்தகைய நிலைமையில், நொதியின் வினைக்கு ஆளாகாத பிணைக்கப்பட்ட மற்றும் பிணைக்கப்படாத அடி மூலக்கூறு ஒப்புமை நொதி கட்டமைப்பைத் தீர்மானிப்பதில் இது உதவியாக இருக்கிறது.
எல்லா உயிரிய வினையூக்கியும் புரத நொதியாக இருப்பதில்லை; RNA-ஆதார வினையூக்கிகளான ரிபோஸைம்கள் மற்றும் ரிபோசோம்கள், RNA புரியிணைதல் மற்றும் உருமாற்ற்ம் போன்ற பல உயிர்மங்களான செயல்பாடுகளுக்கு மிக அத்தியாவசியமானதாக இருக்கிறது. ரிபோசைம்கள் மற்றும் நொதிகளுக்கிடையே முக்கிய வேறுபாடாக இருப்பது, RNA வினையூக்கிகள் நியூக்ளியோட்டைடுகளால் உருவாக்கப்பட்டிருக்கிறது ஆனால் நொதியோ அமினோ அமிலங்களால் உருவாக்கப்பட்டிருக்கிறது. ரிபோசைம்கள் மிகவும் வரையறுக்கப்பட்ட தொகுப்பான வினைகளையும் கூட நிகழ்த்துகின்றன, இருந்தபோதிலும் அவற்றின் வினை இயக்கமுறைகள் மற்றும் இயக்கவியல் அதே வழிமுறைகளால் மதிப்பீடு செய்யப்படவும் பகுக்கப்படவும் முடியும்.
.svg)
ஒரு நொதியால் வினையூக்கம் பெற்ற வினையானது, வினையூக்கமேற்படாத வினையைப் போலவே அதே வினைபடுபொருட்களைப் பயன்படுத்துகிறது மற்றும் அதே ஆக்கப்பொருட்களை உற்பத்தி செய்கிறது. மற்ற இதர வினையூக்கிகள் போல, அடி மூலக்கூறு மற்றும் ஆக்கப்பொருட்களுக்கு இடையிலான் சமநிலையை நொதி மாற்றியமைப்பதில்லை.[1] எனினும், வினையூக்கமேற்படாத வினைகள் போலல்லாமல் நொதி-வினையூக்கம் பெற்ற வினைகள் நிறைவுற்ற இயக்கவியலைக் காட்சிப்படுத்துகின்றன. குறிப்பிட்ட நொதிச் செறிவு மற்றும் ஒப்பீட்டளவில் குறைந்த அடி மூலக்கூற்றுச் செறிவுகளுக்கு, வினை விகிதம் அடி மூலக்கூறு செறிவுடன் நேர்கோட்டில் அதிகரிக்கிறது; நொதி மூலக்கூறுகள் வினைகளை வினையூக்கப்படுத்த பெரும்பாலும் எந்தக் கட்டுப்பாடுகளையும் கொண்டிருப்பதில்லை, மேலும் அடி மூலக்கூற்றுச் செறிவை அதிகரிப்பது என்பது நொதி மற்றும் அடிப்படை மூலக்கூறு ஒன்றை மற்றொன்று எதிர்கொள்ளும் விகிதத்தை அதிகரிப்பதாகும். எனினும், ஒப்பீட்டளவில் உயர்ந்த அடி மூலக்கூற்று செறிவுகளில், வினை விகிதம் அணுகல் வழியாக கற்பிதமான அதிகபட்சத்தை அடைகிறது; நொதி வினைபுரி இடங்கள் அனைத்தும் பெரும்பாலும் நிறைவுற்றிருக்கிறது மேலும் வினைபுரியும் விகிதம் நொதியின் உள்ளார்ந்த பரிமாற்ற விகிதத்தால் முடிவுசெய்யப்படுகிறது. இவ்விரு வரையறுக்கும் நிலைமைகளுக்கு இடையில் இருக்கும் அடி மூலக்கூற்று செறிவு K M என்று குறிப்பிடப்படுகிறது.
ஒரு நொதியின் இரு மிக முக்கிய இயக்கப் பண்புகளாக இருப்பது, ஒரு குறிப்பிட்ட அடி மூலக்கூற்றுடன் ஒரு நொதி எவ்வளவு விரைவாக நிறைவுறுகிறது என்பதும் அது சாதிக்கக்கூடிய மிக அதிகபட்ச விகிதமும் ஆகும். இந்தப் பண்புகளை அறிந்திருப்பது, உயிரணுவில் ஒரு நொதி என்னவெல்லாம் செய்யும் என்பதை அறிவுறுத்தும் மற்றும் இந்நிலைமைகளில் ஏற்படும் மாற்றங்களுக்கு நொதி எவ்வாறு செயற்படும் என்பதையும் காட்டும்.
நொதி மதிப்பீடுகள் என்பது நொதி வினைகளின் விகிதத்தை மதிப்பிடும் பரிசோதனைக்கூட செயல்முறைகளாகும். நொதிகள் தாம் வினையூக்கப்படுத்தும் வினைகளால் நுகரப்படாததால், வினையின் விகிதத்தை அளவிடுவதற்கு நொதி மதிப்பீடுகள் வழக்கமாக அடி மூலக்கூறு அல்லது ஆக்கப்பொருட்களின் செறிவுகளில் ஏற்படும் மாற்றங்களைக் கண்காணிக்கின்றன. அளவிடுவதற்குப் பல்வேறு வழிமுறைகள் இருக்கின்றன. அலைமாலை ஒளிஅளவியல் மதிப்பீடுகள் ஆக்கப்பொருட்கள் மற்றும் வினைபொருட்களுக்கிடையில் ஏற்படும் ஒளியின் அகத்துறிஞ்சல்வலுவின் மாற்றத்தைக் கண்காணிக்கின்றன; கதிர் வீச்சளவியல் மதிப்பீடுகள், காலப்போக்கில் செய்யப்பட்ட ஆக்கப்பொருளை அளவிடுவதற்கான கதிரியக்கத்தின் சேர்க்கை அல்லது வெளியிடலை உட்படுத்தியிருக்கிறது. அலைமாலை ஒளிஅளவியல் மதிப்பீடுகள் தான் மிகவும் வசதியானவை ஏனெனில் வினையின் விகிதத்தைத் தொடர்ச்சியாக அளவிட அது அனுமதிக்கிறது. கதிர் வீச்சளவியல் மதிப்பீடுகளுக்கு மாதிரிகளை (அதாவது அவை தொடராத மதிப்பீடுகளாகும்) நீக்கவும் எண்ணவும் வேண்டிய தேவை இருந்தபோதிலும் அவை வழக்கமாக மிகவும் உணர்ச்சிமிக்கவை மற்றும் நொதி செயல்பாட்டின் மிகக் குறைந்த நிலைகளையே அளவிடமுடியும்.[2] அடி மூலக்கூறு ஒரு ஆக்கப்பொருளாக மாற்றம் செய்யும்போது நிலையான ஓரிடத் தனிமகளின் சேர்க்கை அல்லது வெளியிடுதலைக் கண்காணிப்பதற்குச் செயலொத்த அணுகுமுறையாக இருப்பது பரவலான நிறமாலையியலைப் பயன்படுத்துவதாகும்.
தங்கள் வினைகளை வினையூக்கியாக்கும் ஒற்றை நொதி மூலக்கூற்றில் ஏற்படும் மாற்றங்களைக் கண்காணிப்பதற்கு மிகவும் உணர்ச்சிமிக்க நொதி மதிப்பீடுகள் ஒரு நுண் பெருக்கிக் கண்ணாடி மூலம் குவிமையப்படுத்தப்பட்ட லேசர்களைப் பயன்படுத்துகின்றன. வினையூக்கியின் போது ஏற்படும் அசைவுகளைத் தெரிவிப்பதற்காக இந்த அளவீடுகள் நொதியின் வினைபுரியும் இயக்கமுறையின் போது சார்புக்காரணிகளின் உடனொளிர்வு (fluorescence) களில் ஏற்படும் மாற்றங்களை அல்லது புரதம்|புரதத்தின் குறிப்பிட்ட தலங்களில் சேர்க்கப்பட்டும் உடனொளிர்சாயங்களைப் பயன்படுத்துகின்றன.[3] இந்த ஆய்வுகள், இயக்கவியல் மற்றும் ஒற்றை நொதியின் இயங்கியலைப் பற்றி ஒரு புதிய கண்ணோட்டத்தை வழங்குகிறது, இது பாரம்பரியமிக்க நொதி இயக்கவியலுக்கு எதிரானது, அங்கு மில்லியன் கணக்கிலான நொதி மூலக்கூற்று தொகைகளின் சராசரி நடத்தையைப் பற்றிக் கண்காணிக்கின்றன.[4][5]
நொதி மதிப்பீடுக்கான முன்னேற்ற வளைவின் ஒரு எடுத்துக்காட்டு மேலே காட்டப்பட்டுள்ளது. வினை தொடங்கிய பின்னர் ஒரு குறுகிய காலத்துக்குக் கிட்டத்தட்ட நேராக இருக்கும் துவக்க விகிதத்திலேயே நொதியானது ஆக்கப்பொருட்களைத் தயாரிக்கிறது. வினை தொடர்ந்திருக்க அடி மூலக்கூறு நுகரப்படும்போதே, விகிதாச்சாரம் தொடர்ச்சியாக குறைகிறது (அடி மூலக்கூறு இன்னமும் நிரம்புமட்டத்திலேயே இருக்கும் வரையில்). தொடக்க (மற்றும் பெருமதிப்பு) விகிதத்தை அளவிடுவதற்கு, மொத்த நிறைவேற்றலில் வினை வெறும் சில சதவிகிதமே முன்னேற்றம் கண்ட நிலையிலேயே நொதி மதிப்பீடுகள் மேற்கொள்ளப்படுகின்றன. தொடக்க விகித காலம், மதிப்பீடு நிலைமைகளைச் சார்ந்திருக்கிறது மற்றும் அவை கணப்பொழுதிலிருந்து பல மணிநேரங்கள் வரையில் நீட்டிக்கலாம். எனினும், திரவங்களை அதிவேகமாக கலப்பதற்கான சாதனங்கள், ஒரு வினாடிக்கும் குறைவான தொடக்க விகிதங்களின் மீது வேகமான இயக்கவியல் அளவீடுகளை அனுமதிக்கிறது.[6] முன்னரே நிலையான நிலையில் இருக்கும் இயக்கவியலை அளவிடுவதற்கு இந்த மிக விரைவான மதிப்பீடுகள் அத்தியாவசமாக இருக்கிறது, இவை கீழே விவாதிக்கப்பட்டுள்ளது.
பெரும்பாலான நொதி இயக்கவியல் ஆய்வுகள் இந்த ஆரம்பகட்ட, நொதி வினைகளின் தோராயமான நேரான பாகம் மீது கவனம் செலுத்துகிறது. எனினும், முழுமையான வினை வளைவை அளவிடுவதும் இந்தத் தரவை ஒரு நேரற்ற விகித சமன்பாட்டில் பொருத்துவதும் சாத்தியமானதே. நொதி வினையை இந்த வகையில் அளவிடுவதற்கு முன்னேற்ற-வளைவு பகுப்பாய்வு என்று பெயர்.[7] தொடக்க விகிதம் துல்லியமாக அளவிடப்படமுடியாமல் மிக விரைவாக இருக்கும்போது இந்த அணுகுமுறை விரைவு இயக்கவியலுக்கு ஒரு மாற்றாக மிகவும் பயனுடையதாக இருக்கும்.
ஒற்றை-அடி மூலக்கூறு இயக்கமுறைகளுடன் கூடிய நொதிகளில் உள்ளடங்கியிருப்பவை, டிரையோசுபாசுபேட்ஐசோமிரேசு அல்லது பைசுபோசுபோகிளைசிரேட் மூடேசு போன்ற ஐசோமிரேசுகள், அடினைலேட் சைக்ளேசு மற்றும் சுத்தியல்தலை ரிபோசைம் போன்ற மூலக்கூறக சிதைப்பிகள், ஆர்என்ஏ சிதைப்பி.[8] எனினும், ஒற்றை அடிமூலக்கூற்றை மட்டுமே கொண்டிருக்கும் சில நொதிகள் இந்த வகையான இயக்கமுறைகளின் கீழ் வருவதில்லை. இதற்கான ஒரு உதாரணமாக இருப்பது கேடலேசு, ஹைட்ரஜன் பெராக்சைடு அடி மூலக்கூற்றின் முதல் மூலக்கூறுடன் நொதி வினை புரியும்போது அது உயிர்வளியேற்றப்பட்டதாக ஆகிவிடுகிறது அதன் பின்னர் அது ஒரு அடி மூலக்கூற்றின் இரண்டாவது மூலக்கூறால் குறைக்கப்படுகிறது. ஒரு ஒற்றை அடி மூலக்கூறு ஈடுபட்டபோதிலும், ஒரு மாற்றியமைக்கப்பட்ட நொதி இடைநிலையின் இருப்பு என்பது கேடலேசுவின் இயக்கமுறை உண்மையிலேயே ஒரு பிங்-பாங் இயக்கமுறையாகும், ஒருவகை இயக்கமுறையான இது பன்னிலை-அடி மூலக்கூற்று வினைகள் பிரிவில் கீழே விவாதிக்கப்பட்டுள்ளது.
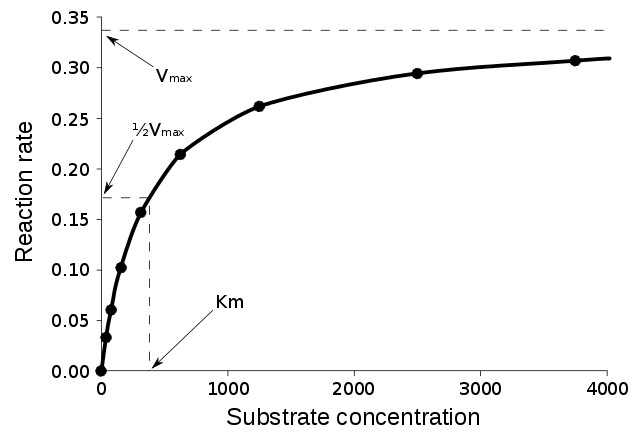
நொதி-வினையூக்கப்படுத்தப்பட்ட வினைகள் நிறைவுகொள்வதால் அவற்றின் வினையூக்கி விகிதம் அதிகரித்துவரும் அடி மூலக்கூற்றுக்கு ஒரு நேரோடியான பின்னூட்டத்தைக் காட்டுவதில்லை. வினையின் தொடக்க விகிதம் வரிசையான பல அடி மூலக்கூற்றுச் செறிவுகளின் மீது அளவிடப்பட்டால் ([S] என குறிப்பிடப்படுகிறது), வலப்புறம் காட்டப்பட்டுள்ளது போல் [S] அதிகரிக்கவும் வினை வீதமும் (v ) அதிகரிக்கும். எனினும், [S] உயர்ந்துகொண்டே போகவும் நொதி அடி மூலக்கூற்றுடன் நிறைவுகொள்கிறது மற்றும் விகிதமானது நொதியின் அதிகபட்ச விகிதமான V max ஐ அடையும்.
ஒற்றை-அடிமூலக்கூற்று வினையின் மிக்கேலிசு-மென்டென் இயக்கம் சார்ந்த மாதிரி வலப்புறம் காட்டப்பட்டுள்ளது. நொதி–அடி மூலக்கூற்று பல்கூட்டுத்தொகுதியான ES ஐ உருவாக்குவதற்கு நொதி E மற்றும் அடி மூலக்கூறு S ஆகியவற்றுக்கு இடையில் ஒரு தொடக்க இருமூலக்கூற்று வினை இருக்கிறது. ஒற்றை மூலக்கூற்று வினையின் நொதிக்குரிய இயக்கமுறை சிறிது சிக்கலாகவே இருந்தாலும், இந்த வினையை வெளிப்படையான ஒற்றை மூலக்கூற்று விகித நிலைஎண் k cat உடன் ஒரு ஒற்றை வினையூக்கும் படிநிலையின் மாதிரியாக ஆக்க அனுமதிக்கும் விகிதம்-முடிவுசெய்யும் ஒரு நொதி படிநிலை இருக்கிறது. வினைப் பாதை ஒன்று அல்லது பல்வேறு இடைநிலைகளைக் கடந்து முன்னேறினால், k cat பல்வேறு தொடக்கநிலை விகித மாறிலியாகச் செயல்படும், அதே நேரத்தில் ஒரு எளிமையான ஒற்றை தொடக்கநிலை வினையில் (எ-டு: எந்த இடைநிலைகளுமற்ற) அது தொடக்கநிலை ஒற்றை மூலக்கூற்று விகித மாறிலி k 2 க்கு ஒத்திருக்கும். வெளிப்படையான ஒற்றை மூலக்கூற்று விகித மாறிலி k cat கொள்முதல் எண் என்றும் அழைக்கப்படுகிறது மேலும் ஒரு வினாடிக்கு வினையூக்கும் நொதிக்குரிய வினைகளின் அதிகபட்ச எண்ணிக்கையைக் குறிக்கிறது.
மிக்கேலிசு-மென்டென் சமன்பாடு[9] (ஆரம்பகட்ட) வினை விகிதம் v 0 அடி மூலக்கூறு-பிணைப்பு சமநிலை மற்றும் விகித மாறிலி k 2
பின்வரும் மாறிலியுடன் எவ்வாறு சார்ந்திருக்கிறது என்பதை விளக்குகிறது.
இந்த மிக்கேலிசு-மென்டென் சமன்பாடுதான் பெரும்பாலான ஒற்றை-அடி மூலக்கூறு நொதி இயக்கவியல்களுக்கு அடிப்படையாக இருக்கிறது. இரு முக்கிய கற்பிதங்கள் இந்தச் சமன்பாட்டுக்குக் கீழிருப்புகளாக இருக்கிறது (எந்த இடைநிலை அல்லது ஆக்கப்பொருள் தடைகளோ ஈடுபடாமல் மற்றும் எந்தவித மாற்றுத்தூண்டுதல் அல்லது ஒத்துழைக்கும் தன்மை இல்லாமல் இயக்கமுறை மட்டுமே என்னும் பொதுவான கற்பிதம் அல்லாமல்). முதல் கற்பிதமாக இருப்பது அரையளவான-நிலைத்திருக்கும்-நிலையிலிருக்கும் கற்பிதம் (அல்லது போலி-நிலைத்திருக்கும்-நிலையிலான கற்பிதக் கொள்கை), அதாவது அடி மூலக்கூறு-கட்டுபடுத்தப்பட்ட நொதியின் செறிவு (அதனால் கட்டுப்படுத்தப்படாத நொதியும் கூட), ஆக்கப்பொருள் மற்றும் அடி மூலக்கூற்றை விட மிக மெதுவாக மாற்றம் கொள்கிறது மேலும் தொகுப்பின் காலப்போக்கில் ஏற்படும் இவ்வாறான மாற்றம் பூச்சியத்திற்குப் பொருத்தப்படலாம். . இரண்டாவது கற்பிதமாக இருப்பது, மொத்த நொதி செறிவும் காலப்போக்கில் மாற்றம் கொள்வதில்லை என்பதாகும், இவ்வாறுபாகுபடுத்தல் தோல்வி (தொடரமைப்புத் தவறு): {\displaystyle {[}E{]}_\text{tot} = {[}E{]} + {[}ES{]} \; \overset{!} } . முழுமையான விளக்கத்தை இங்கு காணலாம்.
மிக்கேலிசு மாறிலி K M அனுபவரீதியாக பின்வருமாறு வரையறுக்கப்பட்டிருக்கிறது, அதாவது நொதி வினையின் விகிதம் பாதியாக இருக்கும் V max செறிவாகும், இது [S] = K m வை மிக்கேலிசு-மென்டென் சமன்பாட்டுக்கு பதிலாக வைத்துச் சரிபார்க்கப்படலாம் மேலும் இது வரைபடமாகவும் பார்க்கப்படலாம். விகிதம் முடிவெடுக்கும் நொதி படிநிலை, அடி மூலக்கூறு கூட்டுப்பிரிவு () வுடன் ஒப்பீட்டளவில் நிதானமாக இருந்தால், மிக்கேலிசு மாறிலி K M தான் ஏறக்குறைய ES தொகுப்பின் கூட்டுப்பிரிவு மாறிலி K D ஆக இருக்கிறது.
உடன் ஒப்பிடுகையில் சிறியதாக இருந்தால் இந்தப் பதம் மற்றும் மிகக் குறைந்த ES தொகுப்பும் உருவாகிறது, இவ்வாறு . இதன் காரணமாக ஆக்கப்பொருள் தோற்றத்தின் விகிதம் இவ்வாறு அமையும்
இவ்வாறு ஆக்கப்பொருளின் உருவாக்க விகிதம் நொதிச் செறிவு மற்றும் அடி மூலக்கூற்று செறிவைச் சார்ந்திருக்கிறது, சமன்பாடு ஒத்திசைவான போலி-இரண்டாம் வரிசை விகித மாறிலி யுடன் இருமூலக்கூறு வினையை ஒத்திருக்கிறது. இந்த மாறிலி, வினையூக்கி பயன்திறனின் ஒரு அளவீடாகும். மிகவும் பயன்திறம் மிக்க நொதி 108 – 1010 M−1 s −1 என்னும் வீச்சில் ஒரு -ஐ அடைகிறது. இந்த நொதி எவ்வளவு திறன்மிக்கதாக இருக்கிறதென்றால், அவை அடிப்படை மூலக்கூறை எதிர்கொள்ளும் ஒவ்வொரு முறையும் அவை வினையை திறம்பட வினையூக்கப்படுத்துகிறது, இவ்வாறு அவை பயன்திறனுக்கான மேல்மட்ட கோட்பாட்டு வரையறையை (பரவல் எல்லை) எட்டியிருக்கிறது; இந்த நொதிகள் அவ்வப்போது கச்சிதமான நொதி என்று குறிப்பிடப்பட்டிருக்கிறது.[10]
மிக்கேலிசு-மென்டென் சமன்பாட்டால் கணித்துரைக்கப்பட்டு கண்காணிக்கப்பட்ட இயக்க வேக அளவுகள் அடி மூலக்கூற்றின் நேர வரிசைமுறை மறைதல் மற்றும் ஆக்கப்பொருளின் உற்பத்தி ஆகியவற்றை மிக்கேலிசு-மென்டென் சமன்பாட்டை முதல் வரிசைமுறை வேதி இயக்கவியல் சமன்பாட்டுக்குள் சேர்ப்பதன் மூலம் நேரடியாக ஒரு முன்மாதிரியாகப் பயன்படுத்தப்படலாம். எனினும், முதல் வரிசைமுறை வேதிய இயக்கவியலின் விவரணையில் இயூலரின் எண்ணைப் பயன்படுத்துவதில் தொடர்புடைய சிக்கலைப் புரிந்துகொள்வதால் மட்டுமே இது சாத்தியப்படும். அதாவது e -k என்பது ஒரு பிளவுப்பட்ட மாறிலி இது கணக்கீடுகளில் ஒரு ஒழுங்கான வழுவை அறிமுகப்படுத்துகிறது மற்றும் ஒவ்வொரு கால வரையறைக்குப் பின்னர் மீதமிருக்கும் அடி மூலக்கூற்றை பிரதிநிதிக்கும் ஒரு ஒற்றை மாறிலியாக மீண்டும் எழுதப்படமுடியும்.[11]
விர்ஜினியா பல்கலைக்கழகத்தில் ஒரு இடைவினை மிக்கேலிசு-மென்டென் இயக்கவியல் பயிற்சியைப் பயன்படுத்தி,[α] வேறுபடும் இயக்கவியல் மாறிலியுடன் கூடிய நொதியின் நடத்தை மீதான விளைவுகள் ஆராயப்படலாம்.
மேலே [S] க்கு எதிராக v யின் இடக்குறியீடு நேர்கோடாக இல்லை; கீழ் [S] யில் ஆரம்பத்தில் நேர்க்கோடாக இருந்தபோதிலும் அது உயர் [S] இல் நிறைவுகொள்ள வளைகிறது. கணினிகளில் நேர்ப்பாங்கற்ற வளைவு-பொருத்தும் நவீன யுகத்திற்கு முன்னர், இந்த நேர்பாங்கின்மை K M மற்றும் V max ஆகியவற்றைத் துல்லியமாக மதிப்பிடுவது கடினமாக்கியிருந்தது. இதனால் பல்வேறு ஆராய்ச்சியாளர்கள், லைன்வீவர்-பர்க் இடக்குறியீடு, இயேடி-ஹாஃப்ஸ்டீ வரைபடம் மற்றும் ஹேன்ஸ்-வூல்ஃப் இடக்குறியீடு போன்ற மிக்கேலிசு-மென்டென் சமன்பாட்டின் நேரியல்பாங்குகளை உருவாக்கினர். இந்த எல்லா நேர்க்கோட்டுப் பிரதிநிதித்துவங்களும் தரவுகளைக் காண்பதற்குப் பயன்படலாம், ஆனால் இயக்க அளவுருகளை முடிவு செய்வதற்கு எதையும் பயன்படுத்தக்கூடாது ஏனெனில் வளைகோட்டுத் தொடர்புப்போக்கு வழிமுறைகள் மூலம் மிகத் துல்லியமான் உறுதிப்பாட்டை அனுமதிக்கும் கணினி மென்பொருள் ஆயத்தமாக கிடைக்கப்பெறுகிறது.[12]
லைன்வீவர்-பர்க் இடக்குறியீடு அல்லது இரட்டை எதிரிடை இடக்குறியீடு தான இயங்கு தரவை விளக்குவதற்கான பொது வழிமுறை. மிக்கேலிசு-மென்டென் சமன்பாட்டின் இரு பக்கங்களின் எதிரிடைகளை எடுத்துக்கொள்வதன் மூலம் உருவாக்கப்படுகிறது. வலப்புறத்தில் காட்டியுள்ளதுபோல் இது மிக்கேலிசு-மென்டென் சமன்பாட்டின் நேர்க்கோட்டு வடிவம் மேலும் இது பின்வரும் சமன்பாட்டுடன் ஒரு நேர் கோட்டை உருவாக்குகிறது y = mx + c இதில் ஒரு y - இடைமறி 1/V max வுக்கு சமமானது மற்றும் -1/K M ஐ பிரதிநிதிக்கும் வரைபடத்தின் இடைமறிப்பான x உடனானது.
இயற்கையாகவே எந்தவொரு பரிசோதனைக்குரிய மதிப்பும் எதிர்மறையான 1/[S] இல் எடுத்துக்கொள்ளக்கூடாது; கீழ்நிலையிலுள்ள வரையறுக்கும் மதிப்பு 1/[S] = 0 (y -இடைமறி) ஒரு முடிவிலா அடி மூலக்கூற்று செறிவுடன் ஒத்திருக்கிறது, இங்கு வலப்புறத்தில் காட்டப்பட்டுள்ளதுபோல் 1/v=1/Vmax ஆக இருக்கிறது; இவ்வாறு, x -இடைமறி உடன்பாடான செறிவுகளில் எடுக்கப்பட்ட பரிசோதனைக்குரிய தரவின் ஒரு புறச் சொருகல் ஆகும். மிகப் பொதுவாகக் கூறுவதென்றால், லைன்வீவர்-பர்க் இடக்குறியீடு குறைந்த அடி மூலக்கூறு செறிவுகளிடத்தில் எடுக்கப்பட்ட அளவீடுகளின் முக்கியத்துவத்தைத் சரித்து விடுகிறது, இவ்வாறு V max மற்றும் K M. ஆகியவற்றின் செம்மையற்ற மதிப்பீடுகளை விளைவிக்கலாம்.[13] மிகவும் செம்மையான நேர்க்கோட்டு இடக்குறியீட்டு வழிமுறையாக இருப்பது இயேடி-ஹாஃப்ஸ்டீ இடக்குறியீடு. இந்நிலையில், v வுக்கு எதிராக v /[S] இடக்குறீயீடு செய்யப்படுகிறது. மூன்றாவது பொதுவான நேர்க்கோட்டு பிரதிநிதியான ஹேன்ஸ்-வூல்ஃப் இடக்குறியில் [S] க்கு எதிராக [S]/v இடக்குறியீடு செய்யப்படுகிறது. மொத்தத்தில், தரவு நெறிப்படுத்தல் பரிசோதனைக்குரிய வேலை அளவைக் குறைக்க உதவும் மற்றும் வெளிப்பாட்டின் நம்பகத்தன்மையை அதிகரிக்கச்செய்யும், மேலும் இது வரைகலை மற்றும் எண் பகுப்பாய்வுக்குப் பொருத்தமாக இருக்கும்.[14]
நொதி இயக்கவியலின் ஆய்வு இரு அடிப்படை காரணங்களுக்கு முக்கியமானதாக இருக்கிறது. முதலில், நொதி எவ்வாறு வேலை செய்கிறது என்பதை விவரிக்க உதவுகிறது, இரண்டாவதாக உயிரினங்களின் நொதி எவ்வாறு நடந்துகொள்கிறது என்பதைக் கணிப்பதற்கு உதவுகிறது. மேலே விவரிக்கப்பட்ட இயக்க மாறிலிகள், K M மற்றும் V max, வளர்ச்சிதைமாற்றத்தை கட்டுப்படுத்த நொதி எவ்வாறு இணைந்து வேலை செய்கிறது என்பதைப் புரிந்துகொள்ளும் முயற்சியில் முக்கியமானதாக இருக்கிறது.
எளிய அமைப்புகளுக்கும் கூட இந்த ஊகங்களைச் செய்வது முக்கியமானது அல்ல. உதாரணத்திற்கு ஆக்சாலோசிடேட் மைட்டோகான்ரியானுக்கு உள்ளாக மாலேடெ டீஹைட்ரோஜீனேசால் உருவாக்கப்படுகிறது. அதன் பின்னர் ஆக்சாலோசிடேட், சிட்ரேட் சிந்தேசு, பாசுபோயினோல்பைருவேட் கார்போக்சிகைனேஸ் அல்லது அஸ்பார்டேட் அமினோடிரான்சுஃபெரேசு ஆகியவற்றால் நுகரப்படலாம், அவை முறையே சிட்ரிக் அமில சுழற்சி, குளூகோனியோஜெனிசிசு அல்லது அசுபார்டிக் அமில உயிரியல் தொகுப்பை உண்ணுகின்றன. எவ்வளவு ஆக்சாலோசிடேட் எந்தப் பாதையில் செல்கின்றன என்பதைக் கணிக்க இயலச் செய்வதற்கு ஆக்சாலோசிடேட் பற்றியும் அத்துடன் இந்த ஒவ்வொரு நொதியின் செறிவு மற்றும் இயக்கவியல் பற்றிய அறிவையும் கொண்டிருக்க வேண்டிய தேவை இருக்கிறது. வளர்சிதைமாற்றத் தடவழியின் நடத்தையைக் கணிக்கும் இந்த நோக்கமானது ஒட்டுமொத்த உயிரினங்களின் கணக்கியல் மாதிரிகளுக்குள் பெரும் அளவிலான இயக்கவியல் மற்றும் மரபணு வெளிப்பாடு தரவின் சேர்க்கைகளில் அதன் மிகக் கடின வெளிப்பாட்டை அடைகிறது. எந்தவொரு நிறைநிலை உயிரிக்கும் இந்தக் குறிக்கோள் எதிர்காலத்தின் மிகத் தொலைவில் இருந்தபோதும், இதைச் சாதிப்பதற்கான முயற்சிகள் இப்போது பாக்டீரியாவில் மேற்கொள்ளப்படுகின்றன, எஸ்செரிச்சியா கோலி வளர்சிதைமாற்ற மாதிரிகளுடன் இப்போது அவை தயாரிக்கப்பட்டு பரிசோதிக்கப்படுகிறது.[15][16]
மிக எளிமையான நிலையையும் ஒருவர் கருத்தில் கொள்ளலாம்
நொதியுடன் கூடிய தொகுதி மற்றும் ஒரு நடுநிலைமை இருக்கும் இடங்களில் மற்றும் இரண்டாவது படிநிலையில் நடுநிலைமை ஒரு ஆக்கப்பொருளாக மாற்றப்படுகிறது. இந்த நிலைமையில் நம்மிடம் மிகவும் ஒத்த சமன்பாடு ஒன்று இருக்கிறது[17]
ஆனால் மாறிலிகள் வேறானவை
நாம் இதை ஒரு வரையறுக்கும் நிலை இல் பார்க்கிறோம், இவ்வாறு EI முதல் E + P வரையிலான இறுதி படிநிலை முந்தைய படிநிலையை விட வேகமாக இருந்தால் நாம் மீண்டும் அதே அசல் சமன்பாட்டைப் பெறுகிறோம். கணக்கியல் ரீதியாக அப்போது நம்மிடம் மற்றும் இருக்கிறது.
பன்முக-அடி மூலக்கூற்று வினைகள், அடி மூலக்கூறுகள் எவ்வாறு மற்றும் எந்த வரிசைமுறையில் பிணைகின்றன என்பதை விவரிக்கும் சிக்கலான விகிதச் சமன்பாடுகளைத் தொடர்கின்றன. அடி மூலக்கூறு A வின் செறிவு நிலையானதாக வைக்கப்பட்டு அடி மூலக்கூறு B யின் செறிவு வேறுபடத்தக்கதாக இருந்தால் இந்த வினைகளின் பகுப்பாய்வு மிகவும் எளிமையானதாகும். இந்நிலைமைகளின் கீழ் நொதியானது ஒரு ஒற்றை-அடி மூலக்கூற்று நொதி போலவே நடந்துகொள்கிறது மேலும் [S] ஆல் ஆன v அடி மூலக்கூறு B வுக்கு தெளிவான K M மற்றும் V max மாறிலிகளை வழங்குகிறது. A வின் வெவ்வேறு நிலையான செறிவுகளில் இந்த நடவடிக்கைகளின் ஒரு தொகுப்பு நிகழ்த்தப்பட்டால் இந்த தரவுகள் வினையின் இயக்கமுறை எது என்பதைக் கண்டறிவதற்குப் பயன்படுத்தப்படலாம். இரு அடி மூலக்கூறு A மற்றும் B யை எடுத்து அவற்றை இரு ஆக்கப்பொருள்களான P மற்றும் Q என மாற்றும் ஒரு நொதிக்கு இருவகையான இயக்கமுறைகள் இருக்கின்றன: டெர்னரி காம்ப்ளக்ஸ் மற்றும் பிங்-பாங்.
இந்த நொதியில், இரு அடிமூலக்கூறுகளும் ஒரே நேரத்தில் நொதியுடன் பிணைந்து EAB முந்நிலை தொகுப்பை உற்பத்தி செய்கின்றன. பிணைந்துகொள்ளும் வரிசைமுறை ஒழுங்கற்றமுறையில் (ஒழுங்கற்ற இயக்கமுறை) அல்லது அடி மூலக்கூறு ஒரு குறிப்பிட்ட வரிசைமுறையில் (ஒழுங்கு வரிசை இயக்கமுறை) இருக்கலாம். முந்நிலை-தொகுப்பு இயக்கமுறையுடன் கூடிய நொதியிலிருந்து v கீழ் [S] வளைவுகளின் (நிலையான A, மாறுபடும் B) ஒரு தொகுப்பு லைன்வீவர்-பர்க் இடக்குறியில் இடக்குறியீடு செயப்பட்டிருந்தால், உருவாகும் கோடுகளின் தொகுப்பு ஒன்றையொன்றுவெட்டும்.
முந்நிலை தொகுப்பு இயக்கமுறையுடன் கூடிய நொதியில் உள்ளடங்குபவை குளூடாதையோன்S - மாற்றுநொதி,[18] டிஹைட்ரோஃபோலேட் ரிடக்டேசு[19] மற்றும் டிஎன்ஏ பல்படியாக்கு நொதி.[20] இப்பின்வரும் இணைப்புகள் நொதி டிஹைட்ரோஃபோலேட் ரிடக்டேசு[β] மற்றும் டிஎன்ஏ பல்படியாக்கு நொதிகளின் முந்நிலை தொகுப்பு இயக்கமுறைகளின் குறும் அசைப்படங்களைக் காட்டுகின்றன.[γ].
வலப்புறத்தில் காட்டியுள்ளதுபோல், பிங்-பாங் இயக்கமுறையுடன் கூடிய நொதி இரு நிலைகளில் தன் இருப்பைக் கொண்டிருக்கலாம், அதாவது E மற்றும் ஒரு வேதியமுறையில் மாற்றம் கொண்ட வடிவமான நொதி E*; இந்த மாற்றியமைக்கப்பட்ட நொதி இடைநிலை நொதி என்று அறியப்படுகிறது. அத்தகைய இயக்கமுறைகளில் அடி மூலக்கூறு A பிணைந்துகொண்டு, ஒரு வேதியக் குழுவை வினைபுரியும் இடத்துக்கு மாற்றல் செய்வதன் மூலம் நொதியை E* ஆக மாற்றுகிறது, பின்னர் அது வெளியிடப்படுகிறது. முதல் அடி மூலக்கூறு வெளியிடப்பட்ட பிறகுதான் அடி மூலக்கூறு B பிணைந்துகொண்டு மாற்றியமைக்கப்பட்ட நொதியுடன் செயல்பட வைத்து, மாற்றியமைக்கப்படாத E வடிவத்தை மீண்டும்உயிர்ப்பிக்கமுடியும். பிங்-பாங் இயக்கமுறையுடன் கூடிய நொதியிலிருந்து v கீழ் [S] வளைவுகளின் (நிலையான A, மாறுபடும் B) ஒரு தொகுப்பு {1}லைன்வீவர்-பர்க் இடக்குறியில்{/1} இடக்குறியீடு செயப்பட்டிருந்தால், உருவாகும் வரித் தொகுப்பான இணைக் கோடுகள் உருவாகும். இது இரண்டாம்நிலை இடக்குறியீடு என அழைக்கப்படும்.
பிங்-பாங் இயக்கமுறைகளுடன் கூடிய நொதியில் உள்ளடங்கியிருப்பவை, தையோரிடாக்சின் பெராக்சிடேசு போன்ற சில ஆக்சிடோரிடக்டேசுகள்,[21] அசைல்நியூராமினேட் சைடைடிலைல்டிரான்சுஃபெரேசு போன்ற டிரான்சுஃபெரேசுகள்[22] மற்றும் டிரைபிசின், சைமோடிரைபிசின் போன்ற செரைன் புரோடேசுகள்.[23] செரைன் புரோடேசுகள் மிகப் பொதுவான மற்றும் பலவகைப்பட்ட நொதி குடும்பத்தைச் சார்ந்தவை, அவற்றில் செரிமான நொதிகள் (டிரைபிசின், கைமோடிரைபிசின் மற்றும் எலாசுடேசு), இரத்த உறைவு இடையிணைப்பின் பல்வேறு நொதிகள் மற்றும் பல உள்ளடங்கியிருக்கின்றன. இந்த செரைன் புரோடேசுகளில் E* இடைநிலை ஒரு அசைல்-நொதி வகையைச் சார்ந்தது, இது புறத அடி மூலக்கூற்றில் இருக்கும் புரத உட்பிணைப்பு மீது ஒரு செயல்படும் இட செரைன் எச்சத்தின் தாக்குதலால் உருவாகிறது. கைமோடிரைபிசின் இயக்கமுறையைக் காட்டும் ஒரு குறும் அசைப்படத்திற்கான இணைப்பு இங்குக் கொடுக்கப்பட்டிருக்கிறது.[δ]
சில நொதிகள் வளைந்த v கீழ் [S] இடக்குறியீட்டை உருவாக்குகிறது, இது செயல்படும் இடத்துக்கான அடி மூலக்கூற்றின் ஒருங்கிணைந்த பிணைப்பை அடிக்கடி சுட்டுகிறது. அப்படியென்றால் ஒரு அடிப்படை மூலக்கூறின் பிணைப்பு அடுத்துவரும் அடிப்படைக்குரிய மூலக்கூறைப் பாதிக்கிறது என்று பொருள். பல்வேறு ஊடாடு செயல்பாட்டுத் தளங்களைக் கொண்ட மல்டிமெரிக் நொதிகளில் இந்த நடத்தை மிகச் சாதாரணமானதுதான்.[24] இங்கு ஒத்துழைக்கும் இயக்கமுறை இரத்தச் சிவப்பணுவினுடையதை ஒத்திருக்கிறது, இங்கு ஒரு செயல்படுமிடத்துடன் அடி மூலக்கூறு பிணைந்துகொண்டு, அடிப்படை மூலக்கூறுக்கான செயல்படுமிடங்கள் இதர செயல்படுமிடங்களின் இணக்கத்தை மாற்றியமைக்கிறது. முதல் அடிப்படைக்குரிய மூலக்கூறு பிணைப்பு அடிமூலக்கூறுக்கான இதர செயல்படுமிடங்களின் இணக்கத்தை அதிகரிக்கும் போது உடன்பாடான ஒத்துழைக்கும்தன்மை ஏற்படுகிறது. முதல் அடிப்படைக்குரிய மூலக்கூறு பிணைப்பு இதர அடிப்படை மூலக்கூறுக்கான நொதியின் இணக்கத்தை குறைக்கும் போது எதிரமறையான ஒத்துழைக்கும்தன்மை ஏற்படுகிறது.
மாற்றுத்தூண்டு நொதிகளில் உள்ளடஙகியிருப்பவை, பாலூட்டிக்குரிய டைரோசைல் tRNA-சிந்தடேசும், இது எதிர்மறையான ஒத்துழைப்புத்தன்மையைக் காட்டுகிறது,[25] மற்றும் நுண்ணுயிரி ஆசுபார்டேடு டிரான்சுகார்பாமோயிலேசு[26] மற்றும் பாசுபோபிரக்டோகைனேசு,[27] இது உடன்பாடான ஒத்துழைப்புத்தன்மையைக் காட்டுகிறது.
ஒத்துழைப்புத்தன்மை வியக்கத்தகும் வகையில் சாதாரணமாகக் காணப்படுகிறது மேலும் நொதி தன்னுடைய அடி மூலக்கூறின் செறிவுகளில் ஏற்படும் மாற்றங்களுக்கான எதிர்ச்செயல்களைக் கட்டுப்படுத்த உதவக்கூடும். உடன்பாடான ஒத்துழைப்புத்தன்மை நொதியை [S] உடன் இன்னும் கூடுதலான உணர்ச்சிமிக்கதாக ஆக்குகிறது மேலும் அவற்றின் செயல்பாடுகள் அடி மூலக்கூறு செறிவின் குறுகிய பரப்பெல்லையில் பெரும் மாற்றங்களைக் காட்டலாம். இதற்கு நேரெதிராக எதிர்மாறான ஒத்துழைப்புத்தன்மை [S] இல் ஏற்படும் சிறு மாற்றங்களுக்கும் நொதியை உணர்வற்றதாக ஆக்குகிறது.
மிக்கேலிசு-மென்டென் அற்ற இயக்கவியலில் இருக்கும் ஒத்துழைப்புத்தன்மையை அளவறிதற்குரிய விகிதத்தை விவரிப்பதற்கு ஹில் சமன்பாடு[28] அடிக்கடி பயன்படுத்தப்படுகிறது. பெறப்பட்ட ஹில் குணகமான n , ஒரு செயல்படுமிடத்தின் அடி மூலக்கூறு பிணைப்பு மற்றொரு செயல்படுமிடத்தில் அடி மூலக்கூறு பிணைப்பை எந்த அளவுக்குப் பாதிப்படையச் செய்கிறது என்பதை அளவிடுகிறது. <1 இன் ஹில் குணகம் எதிர்மாறான ஒத்துழைப்புத்தன்மையைக் குறிக்கிறது மற்றும் >1 இன் குணகம் உடன்பாடான ஒத்துழைப்புத்தன்மையைக் குறிக்கிறது.
ஒரு நொதி அடி மூலக்கூறுடன் கலந்த பின்னர் அந்த முதல் பொழுதில் எந்த ஆக்கப்பொருளும் உருவாக்கப்படவில்லை மற்றும் எந்த இடைநிலைகளும் இருப்பதில்லை. விளைவின் அடுத்த சில கனநொடிகளின் மீதான ஆய்வுகள் முன்னரே நிலைத்த நிலையில் இருக்கும் இயக்கவியல்கள் என்றழைக்கப்படுகிறது. அதனால் முன்னரே நிலைத்த நிலையில் இருக்கும் இயக்கவியல்கள் நொதி–அடி மூலக்கூறு இடைநிலைகள் (ES அல்லது E* போன்றவை) அவற்றின் நிலைத்த நிலையில் இருக்கும் செறிவுகள் கிடைக்கப்பெறும் வரையில் அவற்றின் உருவாக்கம் மற்றும் நுகர்வின் மீது கவனம்செலுத்துகிறது.
இந்த அணுகுமுறை முதன் முதலில் சைமோடிரைபிசினால் வினையூக்கப்பட்ட நீர்ப்பகுப்பு வினைகளுக்குப் பொருத்தப்பட்டது.[29] ஒரு நொதி எந்த இயக்கமுறையை பின்பற்றுகிறது என்பதை ஆய்வு செய்வதில் ஒரு இடைநிலையின் கண்டுபிடிப்பு அவ்வப்போது ஒரு முக்கிய சாட்சியாக இருக்கிறது. உதாரணத்திற்கு, மேலே காட்டபட்டுள்ள பிங்-பாங் இயக்கமுறைகளில் விரைவான இயக்கவியல் அளவீடுகள் ஆக்கப்பொருள் P யின் வெளிப்பாட்டைப் பின்தொடர்ந்து மாற்றியமைக்கப்பட்ட நொதி இடைநிலை E* யின் உருவாக்கத்தை அளவிடுகிறது.[30] சைமோடிரைபிசின் வழக்கில், செயல்படுமிடங்களில் நியூக்ளியோபிலிக் செரைன் மற்றும் அசைல்-நொதி இடைநிலை உருவாக்கத்தால் அடி மூலக்கூறு மீதான தாக்குதலால் இந்த இடைநிலை தோன்றுகிறது.
வலப்புறத்தில் இருக்கும் தோற்றத்தில், வினைபுரியும் முதல் சில வினாடிகளிலேயே நொதி E* ஐ விரைவாக உருவாக்குகிறது. நிலைத்த நிலையை அடைந்தவுடன் விகிதம் குறைந்துவிடுகிறது. வினைபுரிதலின் இந்த விரைவான வெடிப்பு கட்டம் நொதியின் ஒரு ஒற்றை முழுத்தொகுதியை அளவிடுகிறது. இதன் விளைவாக, வரைபடத்தில் y மையக் கோட்டின் இடைமறியாக காட்டப்படும் இந்த வெடிப்பில் வெளியிடப்பட்ட ஆக்கப்பொருளின் அளவு, மதிப்பீட்டில் காணப்படும் செயல்பாட்டு நொதியின் அளவையும் கூட கொடுக்கிறது.[31]
நொதி இயக்கவியலை அளவிடும் ஒரு முக்கிய நோக்கமாக இருப்பது நொதி வினையின் வேதிய இயக்கமுறையை அளவிடுவதாகும், அதாவது அடி மூலக்கூறை ஆக்கப்பொருளாக மாற்றும் வேதியியல் படிநிலையின் வரிசைமுறையை அளவிடுவதாகும். மேலே விவாதிக்கப்பட்ட இயக்கவியல் அணுகுமுறைகள் எந்த விகிதத்தில் இடைநிலைகள் உருவாக்கப்படுகிறது மற்றும் உள்ளுக்குள்ளாக மாற்றப்படுகிறது என்பதைக் காட்டும், ஆனால் இந்த இடைநிலைகள் உண்மையிலேயே என்ன என்று அவற்றால் அடையாளங்காணமுடியாது.
பல்வேறு தீர்வு நிலைமைகளில் அல்லது சற்றே மாற்றியமைக்கப்பட்ட நொதி அல்லது அடி மூலக்கூறின் கீழ் எடுக்கப்படும் இயக்கவியல் அளவீடுகள், இந்த வேதிய இயக்கமுறை மீது அவ்வப்போது வெளிச்சம் போட்டுக் காட்டுகின்றன, ஏனெனில் வினையில் அவை விகிதம்-முடிவுசெய்யும் படிநிலை அல்லது இடைநிலையை வெளிப்படுத்துகிறது. உதாரணத்திற்கு, ஹைட்ரஜன் அணுவுக்கு சகப்பிணைப்பை உடைப்பது ஒரு பொதுவான விகிதம்-முடிவுசெய்யும் படிநிலையாகும். இயலக்கூடிய எந்த ஹைட்ரஜன் மாற்றல்கள் விகிதம் முடிவுசெய்யக்கூடியது என்பதை, ஒவ்வொரு ஹைட்ரஜனும் அதனுடைய திடப்பொருள் ஓரிடத் தனிமம் டியூடெரியம்மால் மாற்றியிடுவதால் ஏற்படும் இயக்கவியல் விளைவுகளை அளவிடுவதன் மூலம் காட்டலாம். முதன்மை இயக்கவியல் ஓரிடத் தனிமம் விளைவு காரணமாக இக்கட்டான ஹைட்ரஜன் மாற்றியிடப்படும்போது விகிதம் மாற்றம் கொள்ளும், இவ்வாறு ஏன் ஏற்படுகிறதென்றால் ஹைட்ரஜனுக்கான பிணைப்புகளை உடைப்பதைக் காட்டிலும் டியூடெரியமுக்கான பிணைப்பை உடைப்பது கடினமாக இருக்கிறது.[32] 13C/12C மற்றும் 18O/16O போன்ற இதர ஓரிடத் தனிம மாற்றுகளுடன் ஒத்த விளைவுகளை அளவிடவது கூட சாத்தியமானதே, ஆனால் இந்த விளைவுகள் இன்னும் நுண்ணியம் வாய்ந்தவை.[33]
இறுதி ஆக்கப்பொருளில் அடிப்படை மூலக்கூறின் பல்வேறு பாகங்களின் விளைவை வெளிப்படுத்துவதற்கும் கூட ஓரிடத் தனிமம் பயன்படுத்தப்படலாம். உதாரணத்திற்கு, இறுதி ஆக்கப்பொருளில் ஆக்சிஜன் அணுவின் மூலத்தைப் பிரித்தறிவது சிலநேரங்களில் கடினமாக இருக்கிறது; ஏனெனில் அது நீரிலிருந்து வந்திருக்கலாம் அல்லது அடி மூலக்கூறு பாகத்திலிருந்தும் வந்திருக்கலாம். வினையில் பங்குபெறும் பல்வேறு மூலக்கூறுகளுக்குள் ஆக்சிஜனின் திடப்பொருள் ஓரிடத் தனிமமான 18O வை ஒழுங்குமுறையில் மாற்றியிடுவதன் மூலமும் ஆக்கப்பொருளில் ஓரிடத் தனிமத்துக்காகப் பரிசோதிப்பதன் மூலமும் இது முடிவுசெய்யப்படுகிறது.[34] வெவ்வேறு pH நிலைமைகளின் கீழ் இயக்கவியல் மற்றும் ஓரிடத் தனிம விளைவுகளை ஆராய்வதன் மூலமும் வேதிய இயக்கமுறையை விளங்கச் செய்ய முடியும்,[35] உலோக அயனி அல்லது இதர சார்புக் காரணிகளை மாற்றியமைப்பதன் மூலமும்,[36] காப்புற்ற அமினோ அமில எச்சங்களான புலம்-வழிநடத்திய முடாஜெனிசிசு மூலமும் அல்லது அடி மூலக்கூறுகளின் ஒத்த அமைப்புச் செயலிகளின் முன்னிலையில் நொதியின் நடத்தையை ஆய்வு செய்வதன் மூலமும்[37] இது சாத்தியப்படும்.
நொதி மட்டுப்படுத்திகள் என்பது நொதிச் செயல்பாடுகளைக் குறைக்கும் அல்லது நீக்கும் மூலக்கூறுகளாகும், நொதியின் வினையூக்க விகிதத்தை அதிகரிக்கும் மூலக்கூறாக இருப்பதால் நொதி வினையூக்கிகள் நாணயத்தின் எதிர்ப் புறமாகக் கருதப்படும். இந்த இடையீட்டு வினைகள் மீளக்கூடியவை (அதாவது மட்டுப்படுத்திகளை நீக்குவது நொதிச் செயல்பாட்டை மீட்டெடுக்கும்) அல்லது மீளும் தன்மையற்றவை (அதாவது மட்டுப்படுத்திகள் நொதியை நிரந்தரமாக செயலிழக்கச் செய்யும்) என எதுவாகவும் இருக்கலாம்.
மரபுரீதியாக மீளூம் நொதி மட்டுப்படுத்திகள், K m மற்றும் V max மீதான தங்கள் விளைவுகளுக்கேற்ப, போட்டியானவை, போட்டியில்லாதவை, போட்டியற்றவை அல்லது கலவையானவை என வகைப்படுத்தப்பட்டிருக்கிறது. வலப்புறத்தில் காட்டப்பட்டுள்ள தோற்றம் அல்லது கீழே கொடுக்கப்பட்டுள்ள அட்டவணையில் காட்டப்பட்டுள்ளது போல் நொதி E யுடன், நொதி–அடி மூலக்கூற்றுத் தொகுதி ES உடன் அல்லது இரண்டுடனும் மட்டுப்படுத்திகள் பிணைவதால் இந்த வெவ்வேறு விளைவுகள் ஏற்படுகின்றன. மட்டுப்படுத்தி செறிவின் ஒரு செயல்பாடாக நொதி இயக்கவியலை ஆய்வு செய்வதன் மூலம் குறிப்பிட்ட வகை மட்டுப்படுத்தியை விளங்கிக்கொள்ளமுடியும். மட்டுப்படுத்தி செறிவுடன் கூடிய சிறப்புடைய வழிமுறைகளில் வேறுபடும் லைன்வீவர்-பர்கே மற்றும் இயேடி-ஹாஃப்ஸ்டீ இடக்குறியீடுகளை நான்கு வகையான மட்டுப்படுத்திகள் உருவாக்குகின்றன.[13] சுருக்கத்திற்கு இரண்டு அடையாளக் குறிகள் பயன்படுத்தப்படுகிறது:
இங்கு K i மற்றும் Ki முறையே நொதி மற்றும் நொதி–அடி மூலக்கூறு தொகுப்புக்குப் பிணைக்கும் கூட்டுப்பிரிவுமாறிலிகளாக இருக்கின்றன. மீளும் மட்டுப்படுத்திகளின் முன்னிலையில், நொதியின் தோற்றங்களான Km மற்றும Vmax முறையே (α/α') Km and (1/α') Vmax என பொதுவான வழக்குகளுக்குக் கீழே காட்டப்பட்டுள்ளது போல் ஆகின்றன.
| width="10%" align="center" | width="10%" align="center" | மட்டுப்படுத்தி வகைகள் | K m தோற்றம் | V max தோற்றம் |
| K i மட்டும் | () | போட்டியானவை | ||
| K i' மட்டும் | போட்டியில்லாதவை | |||
| K i = K i' | () | போட்டியற்றவை | ||
| K i ≠ K i' | () | கலவை |
நேர்கோடல்லாத பின்னடைவு மேலே இருக்கும் சமன்பாடு விகிதத்தில் நொதி இயக்கவியல் தரவில் பொருந்தி[38] கூட்டுப்பிரிவுமாறிலிகளான K i மற்றும் Ki ஆகியவற்றின் துல்லியமான மதிப்பீடுகளைப் பெறலாம்.
இதற்கு மாற்றாக மட்டுப்படுத்தலுக்கான வரையரைகளுக்கான ஆல்பா குறியீடு மட்டுப்படுத்தும் இயக்கவியலை உருமாதிரியாக்கும் மரபுவழிமுறையில் ஒரு சிக்கலை மூடிமறைக்கிறது. குறிப்பாக போட்டியற்ற வடிவிலான மட்டுப்படுத்திகள், மட்டுப்படுத்தி பிணைப்புகள் வினையின் அதிகபட்ச திசைவேகத்தை நேரடியாக பாதிக்கிறது என்னும் கோட்பாட்டைச் சார்ந்திருக்கிறது, எனினும் சித்தரிக்கப்பட்ட சொல்லாடல் அதிகபட்ச திசைவேகத்திற்கு நேர்மாறானது எனத் தெளிவாகத் தொடர்புப்படுத்துகிறது. ஒரு எளிய மாற்றிஒழுங்கமைத்தல் மட்டுப்படுத்தி பிணைப்பு மற்றும் அதிகபட்ச திசைவேகத்தில் குறைவு ஆகிவற்றுக்கிடையிலான நேரடி உறவை வெளிப்படுத்தும்.
ஒரு பூச்சியத்தைக் கீழே சேர்த்தல் ([I]-[I])
[I]+Ki ஆல் வகுத்தல்
மிக்கேலிசு-மென்டென் சமன்பாடு போலவே, இங்கு வினை விகிதம் அடி மூலக்கூறுடன் இடைவினைபுரியும் நொதித் தொகையின் சதவிகிதத்தைச் சார்ந்திருக்கிறது என்பதை இந்த குறியீட்டுமுறையும் வெளிப்படுத்துகிறது.
அடி மூலக்கூறால் பிணைக்கப்பட்ட நொதித் தொகையின் பின்னம்
மட்டுப்படுத்தியால் பிணைக்கப்பட்ட நொதித் தொகையின் பின்னம்
மட்டுப்படுத்துதலுடன் இடைவினைபுரியும் நொதித் தொகைகளின் சதவிகித விளைவாக ஏற்படுவதுதான் மட்டுப்படுத்துதலின் பாதிப்பாக இருக்கிறது. இந்தச் சமன்பாட்டில் தற்போதைய வடிவில் இருக்கும் ஓரே சிக்கல் என்னவென்றால், மட்டுப்படுத்தும் பிணைப்புடன் நொதி பூரணமான மட்டுப்படுதலை ஏற்றுக்கொள்கிறது ஆனால் உண்மையிலேயே அடி மூலக்கூறு மதிப்பின் 100% மட்டுப்படுத்தல் முதல் >0% மட்டுப்படுத்தல் வரை என பரந்து விரிந்த விளைவுகளைக் கொண்டிருக்கலாம். இதற்குப் பதிலளிக்கும் விதமாக, ஒரு டெல்டா V max பதத்தைச் சேர்ப்பதன் மூலம் வெவ்வேறு மட்டுப்படுதல் அளவை அனுமதிப்பதற்கு இந்தச் சமன்பாடு எளிதாக மாற்றியமைக்கப்படலாம்.
அல்லது
தொகையில் தனிப்பட்ட நொதியுடன் மட்டுப்படுத்தி இடைவினை புரியம்போது இருக்கும் எஞ்சிய நொதிக்குரிய் செயல்பாட்டை இந்த பதம் விளக்கலாம். எனினும் இந்தப் பதத்தை உள்சேர்ப்பது, இரண்டாம் நிலை V max பதம் ஆரம்பக்கட்ட பதத்தைவிட அதிகமாக இருக்கம் பட்சத்தில் வினையூக்கத்தின் இயல்தன்மையை அனுமதிக்கும் கூடுதல் மதிப்பைக் கொண்டிருக்கும். வினையூக்கத்தின் இயல்தன்மை மற்றும் குறியீடுக்குக் காரணம் கூறும் விதமாக மட்டுப்படுத்தி "I" ஐ இங்கு "X" என குறிப்பிடப்படும் ஒரு மாற்றியமைப்பியைக் கொண்டு மாற்றியிட்டு மீண்டும் எழுதப்படலாம்.
இந்தச் சொற்தொகுதி மிக்கேலிசு-மென்டென் சமன்பாட்டின் அதிகபட்ச திசைவேகத்திற்குத் தொடர்புடைய இயக்கவியல் விளைவுகளை எளிமையான வழிமுறையில் கையாளும் விளைவை ஏற்படுத்தும் அதே வேளையில், அது K m தொடர்புடைய விளைவுகளை விவரிப்பதற்குப் பயன்படத்தப்படும் சொல்லுக்கான சாத்தியமுள்ள சிக்கல்களையும் அழுந்தக்கூறுகிறது. அடி மூலக்கூறுக்கான நொதி இணக்கத்துடன் தொடர்புடைய K m பெரும்பாலான வழக்குகளில் நொதியின் பிணைப்பு இடத்திற்கான சாத்தியப்படும் மாற்றங்களுக்குத் தொடர்புடையதாக இருக்கவேண்டும், இது நொதி மட்டுப்படுத்தி இடைவினைகளிலிருந்து நேரடியாக ஏற்படும். இவ்வாறாக V max ஐ ஒழுங்குபடுத்துவதற்கு மேலே பரிந்துரைக்கப்பட்டதற்கு இணையான ஒரு பதம் பெரும்பாலான சூழல்களுக்கு ஏற்றதாக இருக்கவேண்டும்.:[39]
நொதி மட்டுப்படுத்திகளும் கூட மீளா அளவுக்கு நொதியை செயலிழக்கச் செய்யும், இது வழக்கமாக செயல்புரியும் இடத்து எச்சங்களை சகப்பிணைப்பாக மாற்றியமைப்பதன் மூலம் செய்யப்படுகிறது. தற்கொலை அடி மூலக்கூறு என்று அழைக்கப்படக்கூடிய இந்த வினைகள், அடுக்குக்குறித்தேய்வு சார்புகளைப் பின்பற்றுகின்றன மற்றும் அவை வழக்கமாக நிறைவுகொள்ளத்தக்கவை. நிறைவுகொள்ளலுக்கு கீழே, மட்டுப்படுத்தியைப் பொருத்தவரையில் அவை முதல் வரிசைமுறை இயக்கவியலைப் பின்பற்றுகின்றன.
நொதி–அடி மூலக்கூறு இடைவினைக்கான பிரபல மாதிரியாக இருப்பது தூண்டிய பொருத்த மாதிரி.[40] நொதி மற்றும் அடி மூலக்கூறுக்கிடையிலான ஆரம்பகட்ட இடைவினை ஒப்பீட்டளவில் மிகவும் பலவீனமாக இருப்பதாக இந்த உருமாதிரி பரிந்துரைக்கிறது, ஆனால் இந்தப் பலவீன இடைவினைகள் பிணைப்பைப் பலப்படுத்தும் நொதியில் இருக்கும் வெளிவடிவ அமைப்பு மாற்றங்களை விரைவிலேயே தூண்டிவிடுகின்றன. இந்த வெளிவடிவ அமைப்பு மாற்றங்கள், வினையால் மாற்றியமைக்கப்படும் அடி மூலக்கூறுகளில் இருக்கும் வேதியியல் பிணைப்புகளைச் செயல்படும் இடங்களில் இருக்கும் வினையூக்க எச்சங்களின் அருகிலும் கொண்டுவருகின்றன.[41] வெளிவடிவ அமைப்பு மாற்றங்கள், வட்டமுறையிருநிறங்காட்டுந்தன்மை அல்லது இரட்டை முனைவாக்கம் தலையீட்டுமானியைப் பயன்படுத்தி அளவிடப்படலாம். பிணைப்பு ஏற்பட்ட பின்னர், வினைக்கு ஒரு மாற்று வேதியியல் வழிப்பாதையை வழங்குவதன் மூலம் வினையின் தன்மைமாறு நிலையின் ஆற்றலை வினையூக்கியின் ஒன்று அல்லது கூடுதல் இயக்கமுறைகள் குறைக்கின்றன. வினையூக்கியின் இயக்கமுறைகளில் உள்ளடங்குபவை, பிணைப்பு இறுக்கம் மூலமான வினையூக்கி; அண்மை மற்றும் திசை அமைவு மூலம்; வினைபுரி இடத்து புரோட்டான் வழங்கி அல்லது ஏற்பிகள் மூலம்; சகஇணைப்பு வினையூக்கிகள் மற்றும் குவாண்ட்டம் டன்னலிங் மூலமான வினையூக்கி.[30][42]
ஒரு நொதியால் எம்முறையிலான வினையூக்கி பயன்படுத்தப்படுகிறது என்பதை நொதி இயக்கவியலால் நிரூபிக்கமுடியாது. எனினும், சில இயக்கவியல் தரவுகள் இதர தொழில்நுட்பங்களால் ஆராயப்படும் இயலும்தன்மைகளைப் பரிந்துரைக்க முடியும். உதாரணத்திற்கு, வெடிப்பு-கட்டம் முன்னரே-நிலைத்த-நிலையிலான இயக்கவியலுடன் கூடிய பிங்-பாங் இயக்கமுறை இந்த நொதியின் இயக்கமுறையில் சகஇணைப்பு வினையூக்கி முக்கியமானதாக இருக்கலாம் என பரிந்துரைக்கக்கூடும். இதற்கு மாற்றாக, K m மீதல்லாமல் V max மீதான திடமான pH விளைவு கண்டறிதல், வினையூக்கி ஏற்படுவதற்கு வினைபுரி இடத்திலிருக்கும் எச்சம் ஒரு குறிப்பிட்ட அயனியாகும் நிலையில் இருக்கவேண்டும் என்பதைக் குறிக்கலாம்.
α. ^ இணைப்பு: ஊடாடும் மிக்கேலிசு-மென்டென் இயக்கவியல் பயிற்சி (ஜாவா தேவைப்படுகிறது) பரணிடப்பட்டது 2007-03-08 at the வந்தவழி இயந்திரம்
β. ^ இணைப்பு: டைஹைட்ரோஃபோலேட் ரிடக்டேஸ் இயக்க முறை (Gif) பரணிடப்பட்டது 2006-08-20 at the வந்தவழி இயந்திரம்
Γ ^ இணைப்பு: டீஎன்ஏ பாலிமெரேஸ் இயக்கமுறை (Gif) பரணிடப்பட்டது 2006-05-14 at the வந்தவழி இயந்திரம்
Δ ^ இணைப்பு: சைமோட்ரைப்சின் இயக்கமுறை (ஃப்ளாஷ் தேவைப்படுகிறது) பரணிடப்பட்டது 2007-03-19 at the வந்தவழி இயந்திரம்
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
![{\displaystyle v_{0}={\frac {V_{\max[}{\mbox{S}}]}{K_{M}+[{\mbox{S}}]}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5b95905c4ce373fddfc860731fbe53d2dce324d8)
![{\displaystyle {\begin{aligned}K_{M}\ &{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{2}+k_{-1}}{k_{1}}}\approx K_{D}\\V_{\max }\ &{\stackrel {\mathrm {def} }{=}}\ k_{cat}{[}E{]}_{tot}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cdbe20c9acd46f16cd32277ef13fbae56435761b)
![{\displaystyle d{[}ES{]}/{dt}\;{\overset {!}{=}}\;0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1b3e6895e4506bf8353d75418cf27091eb1ef57e)
![{\displaystyle [S]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/292bbb82029aa583c5d2ac5fa1d7e4fedf537d8b)
![{\displaystyle [S]/(K_{M}+[S])\approx [S]/K_{M}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6824a6225dc4d79d295bbdb8f0517c0dd1f1f1c4)
![{\displaystyle [E]_{0}\approx [E]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/39febc25791edf75ee15e9d6b31e4e869bf46f9a)
![{\displaystyle v_{0}\approx {\frac {k_{cat}}{K_{M}}}[E][S]\qquad \qquad {\text{if }}[S]\ll K_{M}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1e3160718ec68c7c63d24a928c5bd7f0f16f1d93)
![{\displaystyle [S]=[S]_{0}(1-k)^{t}\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/93211e467eb88a4ed3ce4b1b8a64f3645c540709)
![{\displaystyle [S]=[S]_{0}(1-v/[S]_{0})^{t}\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fc767ed4ec3fb17dbb2b342b438ca22f3a0c5e15)
![{\displaystyle [S]=[S]_{0}(1-(V_{\max[}S]_{0}/(K_{M}+[S]_{0})/[S]_{0}))^{t}\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d29e711bf38226423c5d45b6d47738477796d98f)
![{\displaystyle {\frac {1}{v}}={\frac {K_{M}}{V_{\max[}{\mbox{S}}]}}+{\frac {1}{V_{\max }}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3dc9af4681099fefe2aa5a0bf39e9f837bb894d4)
![{\displaystyle {\begin{aligned}v_{0}&=k_{cat}{\frac {{[}S{]}{[}E{]}_{0}}{K_{M}^{\prime }+{[}S{]}}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7dfa1cb55ea7c262d15d08c58cafea0f402d2e44)
![{\displaystyle \alpha =1+{\frac {[{\mbox{I}}]}{K_{i}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7d05bffbc19ef9047581c87887ae0eea5c11e7fe)
![{\displaystyle \alpha ^{\prime }=1+{\frac {[{\mbox{I}}]}{K_{i}^{\prime }}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e8b2033b5725a8b85d7425d409192cf11885c199)
![{\displaystyle {\cfrac {V_{\max }}{1+{\cfrac {[I]}{K_{i}}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/77b235af32e059b205f8205c562158c86988b340)
![{\displaystyle {\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{K_{i}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/033f13695d07302c106ac09cbafc690d81f5a5b6)
![{\displaystyle {\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{[I]+K_{i}-[I]}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/42e34b0927bf9484b8a664e022d3fd6ba0ad2326)
![{\displaystyle {\cfrac {V_{\max }}{\cfrac {1}{1-{\cfrac {[I]}{[I]+K_{i}}}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b3c1e590a1ee697acaebbee65eea01ff1acdc12f)
![{\displaystyle V_{\max }-V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8c279152b9fce0341d0b79b769c617c038da50c5)
![{\displaystyle {\cfrac {[S]}{[S]+K_{m}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d4864d15c155b606d4e3c9e6318eda5ba0e38b38)
![{\displaystyle {\cfrac {[I]}{[I]+K_{i}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a1c9c3a9de93daeb179488d6523b7ea9a96e8cba)
![{\displaystyle V_{\max }-\Delta V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/90f5601fefd8114c165ac3dfb739e0642e62610c)
![{\displaystyle V_{\max }1-(V_{\max }1-V_{\max }2){\cfrac {[I]}{[I]+K_{i}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/eebe96aec4c5c5472dde69ce46cf75ed805676fb)
![{\displaystyle V_{\max }1-(V_{\max }1-V_{\max }2){\cfrac {[X]}{[X]+K_{x}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9d29eb761d8d80d1b27749d77cc921c022ce1fa7)
![{\displaystyle K_{m}1-(K_{m}1-K_{m}2){\cfrac {[X]}{[X]+K_{x}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/02d4b89078d0ef0508d2a49553de50dac82e43fe)
