Remove ads
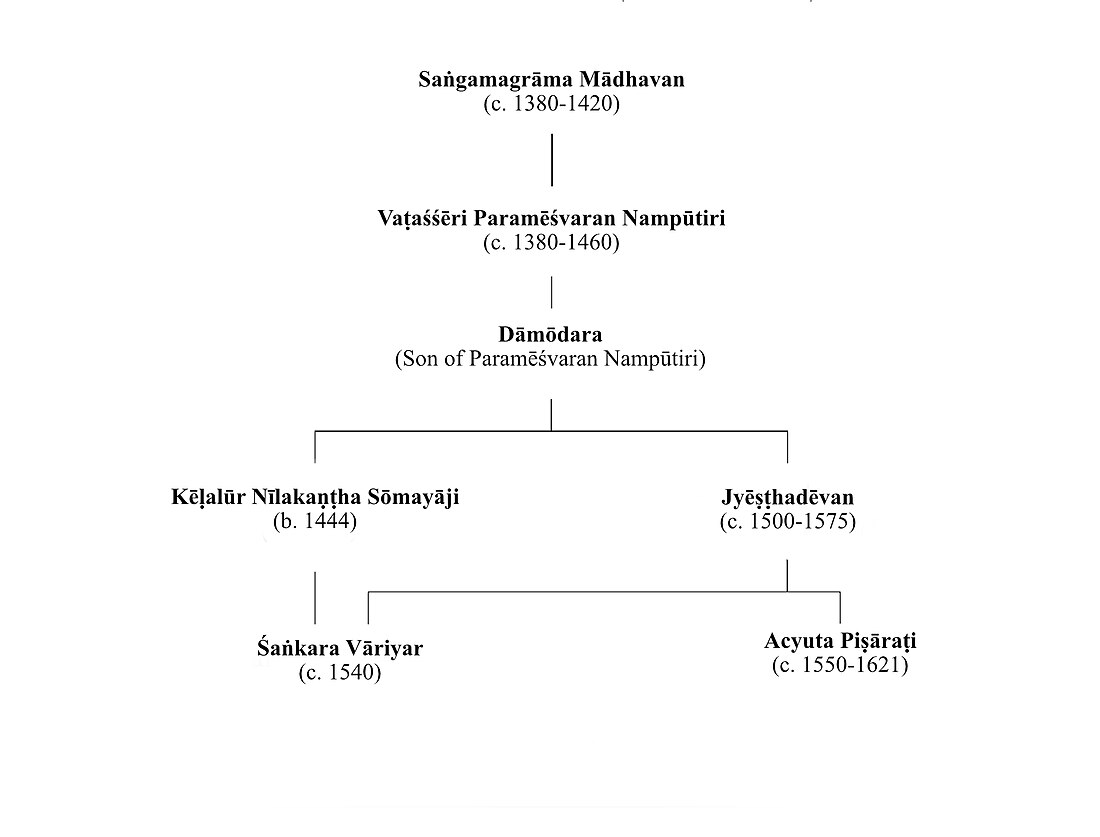
கேரள வானியல் மற்றும் கணிதவியல் பள்ளி, நடு மற்றும் வடக்கு கேரளாவின் வேட்டத்து நாட்டில் அமைந்த தற்கால மலப்புறம் மாவட்டத்தில் 14ம் நூற்றாண்டில் சங்கமகிராம மாதவன் என்பவரால் நிறுவப்பட்டது. இப்பள்ளி 18ம் நூற்றாண்டு வரை செயல்பட்டது. இப்பபள்ளியில் நுண்கணிதம் மற்றும் தொடர் கணிதம் கண்டுபிடிக்கப்பட்டது. இப்பள்ளியின் முக்கிய வானியல் மற்றும் கணிதவியல் அறிஞர்களில் புகழ்பெற்றவர்கள்: சங்கமகிராம மாதவன், வடசேரி பரமேஸ்வரன் நம்பூதிரி, தமோதர நம்பூதிரி, நீலகண்ட சோமயாஜி, ஜேஷ்டதேவர், சங்கர வாரியார் மற்றும் அச்யுத பிஷாரதி ஆவார்.
| கேரள வானியல் மற்றும் கணிதவியல் பள்ளி | |
|---|---|
 கேரள வானியல் மற்றும் கணிதவியல் பள்ளியின் குரு பரம்பரை | |
| அமைவிடம் | |
| நடு மற்றும் வடக்கு கேரளம், இந்தியா | |
| தகவல் | |
| வகை | வானியல், கணிதவியல், அறிவியல் |
| தொடக்கம் | 14ம் நூற்றாண்டு |
| நிறுவனர் | சங்கமகிராம மாதவன் |
| மூடல் | 18ம் நூற்றாண்டு |
Remove ads
நான்காம் நூற்றாண்டில் கேரளாவில் வாழ்ந்த ஜோதிடரும், வானவியலாளருமான வரருச்சி கடபயாதி எண் கணிதத்தை நடைமுறைப்படுத்தினார்.
லீலாவதியும், ஆர்யபாட்டியாவும் கேரளக் கணிதத்தில் உண்மையான நூல்களாகக் கருதப்பட்டது. கிபி 8ம் நூற்றாண்டில், சங்கரநாராயணன் என்ற வானியலாளர் மேற்பார்வையில் கொடுங்கல்லூரில் ஒரு கண்காணிப்பு நிலையம் இருந்தது. இதைத் தொடர்ந்து கேரளாவில் பாபரஹம் என்ற கணக்கீட்டு முறை உருவாக்கப்பட்டது. இதில் சில குறைபாடுகள் இருந்தது. இதைத் தீர்க்க, கிபி 14ம் நூற்றாண்டில் கேரளக் கணிதவியலாளர்கள் 2 முறைகளை முன்வைத்தனர்:
Remove ads
கோள்களின் இயக்கம் தொடர்பான கருத்துகளை மதிப்பாய்வு செய்ய முக்கோணவியலை ஜோத்பதி என்ற பெயரில் உருவாக்கப்பட்ட ஒரு கிளை ஆகும். இந்தக் கிளையானது கேரளக் கணிதவியலாளர்களான சங்கமகிராம மாதவன் மற்றும் நீலகண்ட சோமயாஜி ஆகியோரால் அட்சரேகை கணக்கீடு, நிலை நிர்ணயம், இயக்கம் போன்ற நோக்கங்களுக்காக உருவாக்கப்பட்டது.
விட்டத்தைப் பயன்படுத்தி அதன் சுற்றளவைக் கண்டறிய முடிவிலா தொடர் உருவாக்கப்பட்டது. இதற்கு வழிவகுத்த சில காரணிகள், சுற்றளவு மற்றும் விட்டம் பொதுவான வரம்பைக் கொண்டிருக்கவில்லை, இது முழுமையான மதிப்பைக் கண்டுபிடிக்க முடியாது என்பதைக் கண்டறிய வழிவகுத்தது.
இதன் முக்கியமான கண்டுபிடிப்பு முக்கோணவியல் செயல்பாடுகளுக்கான தொடர் விரிவாக்கம் ஆகும். சமஸ்கிருதத்தில் நீலகண்ட சோமயாஜி எழுதிய தந்திர சம்கிரஹாவில் விவரிக்கப்பட்டுள்ளது. அறியப்படாத ஒரு எழுத்தாளரால் எழுதப்பட்ட தந்திர சம்கிரஹ-வாக்கியம் என்ற புத்தகத்திலும் இது விவரிக்கப்பட்டுள்ளது. அதன் கொள்கைகள் ஆதாரம் இல்லாமல் எழுதப்பட்டன. ஆனால் ஒரு நூற்றாண்டுக்குப் பிறகு, மலையாளப் புத்தகமான லாஜிக்கல் லாங்குவேஜில் ஜேஷ்டதேவர்[1] (1500-1610) அவற்றுக்கான சான்றுகளை (சைன், கொசைன் மற்றும் தலைகீழ் தொடுகோடுகளுக்கான தொடர்) வழங்கினார். ஐரோப்பாவில் நுண்கணிதம் கண்டுபிடிக்கப்படுவதற்கு இரண்டு நூற்றாண்டுகளுக்கு முன்னர், தந்திரச் சுருக்கத்தின் விளக்கத்தில் ஆதாரங்கள் கொடுக்கப்பட்டுள்ளது. அவர்களின் கண்டுபிடிப்புகள் கேரளாவிற்கு வெளியே அறியப்பட்டவை என்பதற்கு எந்த ஆதாரமும் இல்லை.
Remove ads
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads