Bisektris

En bisektris till en vinkel ${\displaystyle \angle ABC}$ är en stråle från B genom en punkt D sådan att ${\displaystyle \angle ABD=\angle DBC}$. En bisektris delar en vinkel i två lika delar (bisektris betyder "dela i två delar"). En vinkel har endast en bisektris. Varje punkt på en vinkels bisektris har samma avstånd till vinkelns sidor. Om en stråle delar en vinkel mindre än ${\displaystyle 180^{\circ }}$ säger man att strålen är en inre bisektris. Den yttre bisektrisen är strålen som delar en vinkels supplementvinkel i två lika delar.

Bisektriserna till en triangel (röda linjer) skär varandra i en punkt

Konstruktion med passare och rätskiva.

För att konstruera en vinkels bisektris med passare och rätskiva dras en cirkel vars centrum är vertex^{[särskiljning behövs]}. Cirkeln korsar vinkelns sidor i två punkter. Med dessa två punkter som centrum, rita två cirklar med samma storlek som den första. Skärningspunkterna för cirklarna bestämmer en stråle som är vinkelns bisektris. Värt att notera är att en godtycklig vinkel^[1] inte kan delas i tre lika stora delar med endast passare och rätskiva (detta bevisades först av Pierre Wantzel).

Triangel

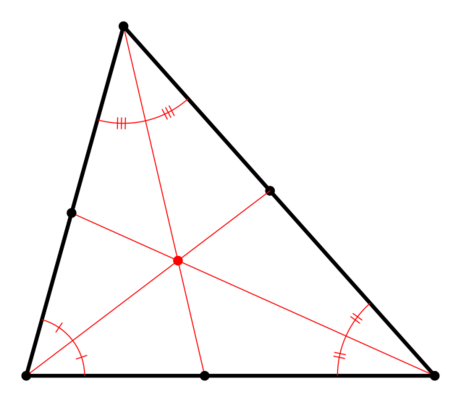
De tre bisektriserna till hörnen i en triangel skär varandra i en punkt, centrum för triangelns inskrivna cirkel. Bisektriserna till en triangel är cevianer. De tre skärningspunkterna med vinklarnas motstående sidor har de trilinjära koordinaterna ${\displaystyle (0,1,1),\ (1,0,1)}$ respektive ${\displaystyle (1,1,0)}$.^[2]

Bisektrissatsen

Figur 1: Bisektrissatsen: b/c = x/y. ${\displaystyle t_{\alpha }}$ betecknar bisektrisens längd

En bisektris delar motstående sida i samma proportioner som längderna av de sidor som bildar den delade vinkeln:

${\displaystyle {\frac {b}{c}}={\frac {x}{y}}\quad }$ (1)

Drag linjen CD parallell med sidan AB och dra ut bisektrisen till skärningspunkten med D (se figur 1). Då är triangeln ACD likbent eftersom dess vinklar i A och D är lika och sidan AC har således samma längd som CD. Trianglarna CDE och ABE är likformiga och sambandet (1) följer.

Bisektrisens längd

Om sidlängderna i en triangel är ${\displaystyle a,b,c,}$ är semiperimetern (halva omkretsen) ${\displaystyle s=(a+b+c)/2}$ och om ${\displaystyle A}$ är motstående hörn till sidan ${\displaystyle a}$, då är längden av bisektrisen till vinkeln ${\displaystyle \alpha }$ i ${\displaystyle A}$ (figur 1):

${\displaystyle t_{a}={\sqrt {bc\left(1-{\frac {a^{2}}{(b+c)^{2}}}\right)}}={\frac {2{\sqrt {b\,c\,s(s-a)}}}{b+c}}}$

Härledning

Med hjälp av bisektrissatsen får vi:

${\displaystyle a=x+y=x+{\frac {cx}{b}}\Leftrightarrow x={\frac {ab}{b+c}}}$ (1) och, likaledes,

${\displaystyle y={\frac {ac}{b+c}}}$ (2)

Stewarts sats ger:

${\displaystyle b^{2}y+c^{2}x=a({t_{a}}^{2}+xy)}$ (3)

Insättning av (1) och (2) i (3) ger

${\displaystyle b^{2}{\frac {ac}{b+c}}+c^{2}{\frac {ab}{b+c}}=a\left({t_{a}}^{2}+{\frac {ab}{b+c}}\cdot {\frac {ac}{b+c}}\right)=a\left({t_{a}}^{2}+{\frac {a^{2}bc}{(b+c)^{2}}}\right)\Leftrightarrow }$

${\displaystyle {\frac {b+c}{b+c}}\cdot abc=a\left({t_{a}}^{2}+{\frac {a^{2}bc}{(b+c)^{2}}}\right)\Leftrightarrow }$

${\displaystyle bc={t_{a}}^{2}+{\frac {a^{2}bc}{(b+c)^{2}}}\Leftrightarrow }$ (ur detta steg fås enkelt ${\displaystyle t_{a}={\sqrt {bc\left(1-{\frac {a^{2}}{(b+c)^{2}}}\right)}}}$.)

${\displaystyle {t_{a}}^{2}=bc-{\frac {a^{2}bc}{(b+c)^{2}}}={\frac {bc(b+c)^{2}-a^{2}bc}{(b+c)^{2}}}={\frac {bc((b+c)^{2}-a^{2})}{(b+c)^{2}}}}$ (4)

Insättning av ${\displaystyle s={\frac {a+b+c}{2}}\Leftrightarrow b+c=2s-a}$ ger vidare

${\displaystyle {t_{a}}^{2}={\frac {bc((2s-a)^{2}-a^{2})}{(b+c)^{2}}}-a^{2}={\frac {bc(4s^{2}-4sa+a^{2}-a^{2})}{(b+c)^{2}}}={\frac {4bcs(s-a)}{(b+c)^{2}}}\Leftrightarrow }$

${\displaystyle t_{a}={\frac {2{\sqrt {b\,c\,s(s-a)}}}{b+c}}}$

Tangentens längd fås också med hjälp av nedanstående trigonometriska funktion,^[3]

${\displaystyle t_{a}={\frac {2bc}{b+c}}\cos {\frac {\alpha }{2}}}$

Härledning

Fås ur (4) ovan, cosinussatsen i formen ${\displaystyle b^{2}+c^{2}-a^{2}=2bc\cdot \cos \alpha }$ och ${\displaystyle \cos \alpha =2\cdot \cos ^{2}{\frac {\alpha }{2}}-1}$ ty

${\displaystyle {\begin{aligned}bc((b+c)^{2}-a^{2})&=bc(b^{2}+c^{2}+2bc-a^{2})=bc(2bc\cdot \cos \alpha +2bc)=\\&=2b^{2}c^{2}(\cos \alpha +1)=2b^{2}c^{2}(2\cdot \cos ^{2}{\frac {\alpha }{2}}-1+1)=4b^{2}c^{2}\cdot \cos ^{2}{\frac {\alpha }{2}}\Rightarrow \end{aligned}}}$

${\displaystyle {t_{a}}^{2}={\frac {bc((b+c)^{2}-a^{2})}{(b+c)^{2}}}={\frac {4b^{2}c^{2}\cdot \cos ^{2}{\frac {\alpha }{2}}}{(b+c)^{2}}}\Leftrightarrow }$

${\displaystyle t_{a}={\frac {2bc\cdot \cos {\frac {\alpha }{2}}}{b+c}}}$

Om bisektrisen till vinkeln ${\displaystyle A}$ i triangeln ${\displaystyle ABC}$ har längden ${\displaystyle t_{a}}$ och delar motstående sida i två delar med längd ${\displaystyle x}$ och ${\displaystyle y,}$ då är

${\displaystyle t_{a}^{2}=bc-xy}$

där ${\displaystyle b}$ och ${\displaystyle c}$ är sidor motstående till hörnen ${\displaystyle B}$ och ${\displaystyle C}$.

Om bisektriserna till vinklarna ${\displaystyle A,}$ ${\displaystyle B}$ och ${\displaystyle C}$ har längderna ${\displaystyle t_{a},}$ ${\displaystyle t_{b}}$ och ${\displaystyle t_{c},}$ då är ^[4]

${\displaystyle {\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(a+c)^{2}}{ac}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}}$

Till tre bisektriser med givna längder finns alltid en och endast en triangel.^[5]

Referenser

Noter

1. Undantag finns för vissa givna vinklar; exempelvis vinklar som är heltalsmultipler av ${\displaystyle \pi /2^{N}}$. Dessa kan delas via en regelbunden sexhörning och successiva halveringar av dennas sidor. För att dela en rät vinkel: Sätt passaren i vinkeln och rita en cirkel som skär de båda vinkelbenen och placera sedan passaren i var och en av dessa skärningspunkter och avsätt cirkelns radie på cirkeln och vinkeln är delad i tre vinklar på vardera 30°. Även femhörningar (och sjuttonhörningar) kan användas.
2. Eric Weisstein, Angle bisector på Wolfram MathWorld.
3. Oxman, Victor, On the existence of triangles with given lengths of one side and two adjacent angle bisectors Arkiverad 23 april 2021 hämtat från the Wayback Machine., Forum Geometricorum 4, 2004, 215–218.
4. Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
5. För ett bevis se Beni Bogoşel, 2010, The Existence of a Triangle with Prescribed Angle Bisector Lengths.