Siksikan congcot

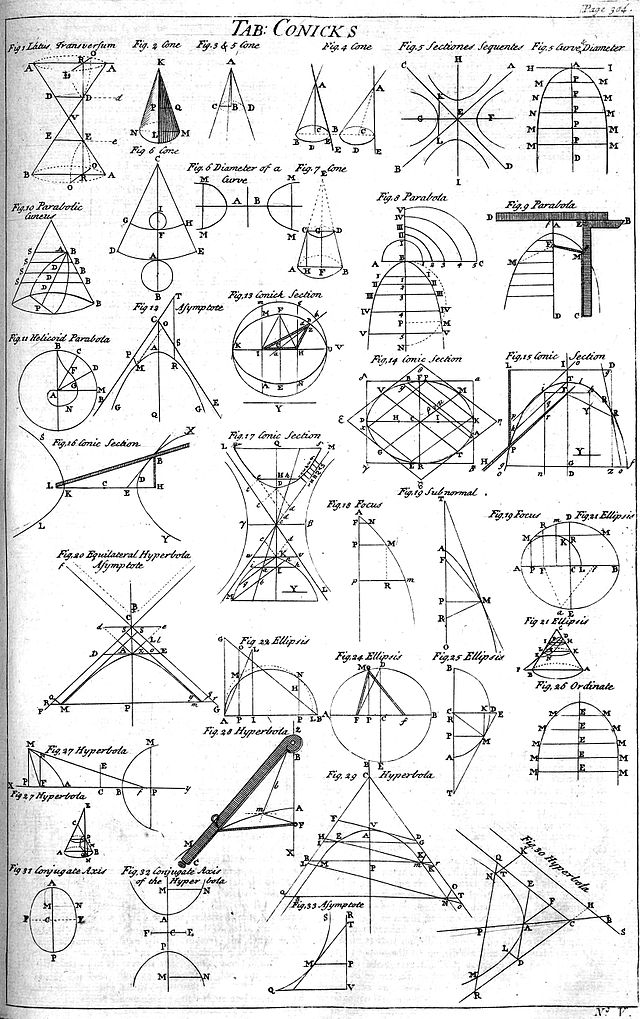
Dina matematika, siksikan congcot atawa keureutan congcot nyaéta lokus ti sakabéh titik anu ngabentuk kurva dua-diménsi, anu kabentuk ku siksikan tina hiji congcot ku hiji widang. Tilu jenis kurva anu mungkin bisa kawangun nyaéta Parabola, Élips, jeung Hiperbola. Apollonius ti Perga mangrupa matematikawan Yunani anu munggaran nalungtik siksikan congcot sacara sistematik dina awal abad ka-2 SM.

Jinis pasingan congcot:
1: Bunderan 2: Elips
3: Parabola 4: Hiperbola

Tabél Cylopedia

Géometri

Géometri siksikan congcot jeung jinis-jinisna

Lamun hayang ngarti kana géometri siksikan congcot, hiji congcot dianggap mibanda dua kulit anu ngawentang nepi ka teu kacumpon di dua-dua arah. Hiji generator mangrupa hiji gurat anu bisa dijieun dina kulit congcot, tur kabéh generator silih papotong-potong dina hiji titik anu disebut vértéks congcot.

Jinis-jinis siksikan congcot

Lamun hiji widang ngeureut congcot sajajar jeung hiji atawa hiji generator wungkul, mangka siksikanna téh parabola. Lamun widang panyiksik sajajar jeung dua generator, mangka siksikannana bakal motong kulit dua-duana jeung ngabentuk hiji hiperbola. Hiji élips kawangun upama widang panyiksikna teu sajajar jeung generator anu mana waé. Bunderan mah kasus husus dina élips, anu kawangun lamun widang panyiksik motong kabéh generator jeung panceg lempeng sumbu congcot.

Kasus dégenerasi

Kasus-kasus dégenerasi bakal kajadian lamun widang-widang panyiksik ngaliwatan vértéks congcot. Keureutan-keureutanna bisa mangrupa titik, gurat lempeng, jeung dua gurat lempeng anu silih papotong-potong. Hiji titik kacipta lamun widang panyiksik ngaliwatan vértéks congcot namung henteu motong generator saeutik-eutik acan. Kasus ieu mangrupa élips anu kadégenerasi. Upama widang panyiksik ngaliwatan vértéks congcot, jeung ngan aya hiji generator, mangka anu bakal kajadian nyaéta hiji gurat lempeng, jeung mangrupa parabola anu kadégenerasi. Hiji hiperbola kadégenerasi lamun widang panyiksik ngaliwat kana vértéks congcot jeung dua generator nepikeun méréan dua gurat lempeng anu silih papotong-potong.

Geometri analitis

Sacara géometri analitis, siksikan congcot bisa diwangenankeun minangka:

perenahna kalungguhan titik-titik dina hiji widang, sakituna, nepikeun jarak titik-titik éta kana hiji titik tetep F (anu disebut fokus) mibanda rasio anu puguh kana jarak titik-titik éta ka hiji gurat tetep L (disebut diréktriks) anu teu ngandung F[1].

Ékséntrisitas nyaéta rasio antara FP jeung P'P.Élips (e=1/2), parabola (e=1) jeung hiperbola (e=2) kalawan fokus (F) jeung diréktriks anu angger.

Rasio anu puguh éta disebut ékséntrisitas, dilambangkeun ku e, jeung mangrupa wilangan non-négatip. Pikeun e = 0, siksikan congcot éta téh nyaéta bunderan, 0 < e < 1 hiji élips, e = 1 hiji parabola, jeung e > 1 hiji hiperbola.

Koordinat Kartésius

Dina koordinat kartésius, grafik tina pasaruaan kuadrat jeung dua variabel osok ngahasilkeun siksikan congcot, jeung kabéh siksikan congcot bisa dihasilkeun maké cara ieu.

Upama nyampak pasaruaan kuadrat anu bentukna:

${\displaystyle ax^{2}+2hxy+by^{2}+2gx+2fy+c=0}$

mangka:

• Lamun h² = ab, pasaruaan ieu ngahasilkeun parabola.
• Lamun h² < ab, pasaruaan ieu ngahasilkeun elips.
• Lamun h² > ab, pasaruaan ieu ngahasilkeun hiperbola.
• Lamun a = b dan h = 0, pasaruaan ieu ngahasilkeun bunderan.
• Lamun a + b = 0, pasaruaan ieu ngahasilkeun hiperbola pasagi.

Bentuk pasaruaan umum

Bentuk pasaruaan umum minangka:

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}$

kacindekan:

• Lamun A = B = 0 mangka pasaruaanna mangrupa gurat lempeng/linear
• Lamun A = B = 0 tapi teu duanana mangka pasaruaanna mangrupa parabola/kuadrat
• Lamun A = B mangka pasaruaanna mangrupa bunderan
• Lamun A ≠ B jeung tandana positip mangka pasaruaanna mangrupa élips
• Lamun A ≠ B jeung tandana négatip mangka pasaruaanna mangrupa hiperbola

Saliwat siksikan congcot

Bunderan

Titik puseur (0,0): ${\displaystyle x^{2}+y^{2}=r^{2}}$

Titik puseur (h,k): ${\displaystyle (x-h)^{2}+(y-k)^{2}=r^{2}}$ atawa ${\displaystyle x^{2}+2hx+h^{2}+y^{2}+2ky+k^{2}-r^{2}=0}$

dengan ${\displaystyle x^{2}+y^{2}+Ax+By+C=0}$ mangka ${\displaystyle A=2h,B=2ksartaC=h^{2}+k^{2}-r^{2}}$

Parabola

	Vértikal	Horisontal
	Titik puseur (0,0)
Pasaruaan	${\displaystyle x^{2}=4py}$	${\displaystyle y^{2}=4px}$
Sumbu simétri	sumbu y	sumbu x
Fokus	${\displaystyle F(0,p)}$	${\displaystyle F(p,0)}$
Diréktris	${\displaystyle y=-p}$	${\displaystyle x=-p}$
	Titik puseur (h,k)
Pasaruaan	${\displaystyle (x-h)^{2}=4p(y-k)}$	${\displaystyle (y-k)^{2}=4p(x-h)}$
Sumbu simétri	${\displaystyle x=h}$	${\displaystyle y=k}$
Fokus	${\displaystyle F(h,k+p)}$	${\displaystyle F(h+p,k)}$
Diréktris	${\displaystyle y=k-p}$	${\displaystyle x=h-p}$

Élips

	Vértikal	Horisontal
	Titik puseur (0,0)
Pasaruaan	${\displaystyle {\frac {x^{2}}{b^{2}}}+{\frac {y^{2}}{a^{2}}}=1}$	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
Panjang sumbu mayor	${\displaystyle 2a}$	${\displaystyle 2a}$
Panjang sumbu minor	${\displaystyle 2b}$	${\displaystyle 2b}$
Panjang Latus Réktum	${\displaystyle L={\frac {2b^{2}}{a}}}$	${\displaystyle L={\frac {2b^{2}}{a}}}$
Fokus	${\displaystyle F(0,\pm c)}$	${\displaystyle F(\pm c,0)}$
Puncak	${\displaystyle P(0,\pm a)}$	${\displaystyle P(\pm a,0)}$
Diréktris	${\displaystyle y=\pm {\frac {a^{2}}{c}}}$	${\displaystyle x=\pm {\frac {a^{2}}{c}}}$
Ékséntrisitas	${\displaystyle e={\frac {c}{a}}}$	${\displaystyle e={\frac {c}{a}}}$
	Titik puseur (h,k)
Pasaruaan	${\displaystyle {\frac {(x-h)^{2}}{b^{2}}}+{\frac {(y-k)^{2}}{a^{2}}}=1}$	${\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}$
Panjang sumbu mayor	${\displaystyle 2a}$	${\displaystyle 2a}$
Panjang sumbu minor	${\displaystyle 2b}$	${\displaystyle 2b}$
Panjang Latus Réktum	${\displaystyle L={\frac {2b^{2}}{a}}}$	${\displaystyle L={\frac {2b^{2}}{a}}}$
Fokus	${\displaystyle F(h,k\pm c)}$	${\displaystyle F(h\pm c,k)}$
Puncak	${\displaystyle P(h,k\pm a)}$	${\displaystyle P(h\pm a,k)}$
Diréktris	${\displaystyle y=\pm {\frac {a^{2}}{c}}}$	${\displaystyle x=\pm {\frac {a^{2}}{c}}}$
Ékséntrisitas	${\displaystyle e={\frac {c}{a}}}$	${\displaystyle e={\frac {c}{a}}}$

anu mana ${\displaystyle c={\sqrt {a^{2}-b^{2}}}}$

Hiperbola

	Vértikal	Horisontal
	Titik puseur (0,0)
Pasaruaan	${\displaystyle {\frac {x^{2}}{b^{2}}}-{\frac {y^{2}}{a^{2}}}=1}$	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
Panjang sumbu mayor	${\displaystyle 2a}$	${\displaystyle 2a}$
Panjang sumbu minor	${\displaystyle 2b}$	${\displaystyle 2b}$
Panjang Latus Réktum	${\displaystyle L={\frac {2b^{2}}{a}}}$	${\displaystyle L={\frac {2b^{2}}{a}}}$
Fokus	${\displaystyle F(0,\pm c)}$	${\displaystyle F(\pm c,0)}$
Puncak	${\displaystyle P(0,\pm a)}$	${\displaystyle P(\pm a,0)}$
Asimtot	${\displaystyle y=\pm {\frac {a}{b}}x}$	${\displaystyle y=\pm {\frac {b}{a}}x}$
Ékséntrisitas	${\displaystyle e={\frac {c}{a}}}$	${\displaystyle e={\frac {c}{a}}}$
	Titik puseur (h,k)
Pasaruaan	${\displaystyle {\frac {(x-h)^{2}}{b^{2}}}-{\frac {(y-k)^{2}}{a^{2}}}=1}$	${\displaystyle {\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1}$
Panjang sumbu mayor	${\displaystyle 2a}$	${\displaystyle 2a}$
Panjang sumbu minor	${\displaystyle 2b}$	${\displaystyle 2b}$
Panjang Latus Rectum	${\displaystyle L={\frac {2b^{2}}{a}}}$	${\displaystyle L={\frac {2b^{2}}{a}}}$
Fokus	${\displaystyle F(h,k\pm c)}$	${\displaystyle F(h\pm c,k)}$
Puncak	${\displaystyle P(h,k\pm a)}$	${\displaystyle P(h\pm a,k)}$
Asimtot	${\displaystyle (y-k)=\pm {\frac {a}{b}}(x-h)}$	${\displaystyle (y-k)=\pm {\frac {b}{a}}(x-h)}$
Eksentrisitas	${\displaystyle e={\frac {c}{a}}}$	${\displaystyle e={\frac {c}{a}}}$

di mana ${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$

Pasaruaan gurat toél

ngagradién ${\displaystyle m}$ (${\displaystyle y=mx+c}$)

	Vértikal	Horisontal
	Titik puseur (0,0)
Bunderan	${\displaystyle y=mx\pm r{\sqrt {1+m^{2}}}}$
Parabola	${\displaystyle y=mx-pm}$	${\displaystyle y=mx+{\frac {p}{m}}}$
Elips	${\displaystyle y=mx\pm {\sqrt {b^{2}+a^{2}m^{2}}}}$	${\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}+b^{2}}}}$
Hiperbola	${\displaystyle y=mx\pm {\sqrt {b^{2}-a^{2}m^{2}}}}$	${\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}$
	Titik puseur (h,k)
Bunderan	${\displaystyle (y-k)=m(x-h)\pm r{\sqrt {1+m}}}$
Parabala	${\displaystyle (y-k)=m(x-h)-pm}$	${\displaystyle (y-k)=m(x-h)+{\frac {p}{m}}}$
Élips	${\displaystyle (y-k)=m(x-h)\pm {\sqrt {b^{2}+a^{2}m^{2}}}}$	${\displaystyle (y-k)=m(x-h)\pm {\sqrt {a^{2}m^{2}+b^{2}}}}$
Hiperbola	${\displaystyle y=mx\pm {\sqrt {b^{2}-a^{2}m^{2}}}}$	${\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}$

Lamun pasaruaan gurat lempeng ngagradién sajajar mangka ${\displaystyle m_{2}=m_{1}}$

Lamun pasaruaan gurat lempeng ngagradién panceg lempeng mangka ${\displaystyle m_{2}={\frac {-1}{m_{1}}}}$

ngaliwatan titik ${\displaystyle (x_{1},y_{1})}$

ku cara bagi adil

	Vertikal	Horisontal
	Titik puseur (0,0)
Bunderan	${\displaystyle xx_{1}+yy_{1}=r^{2}}$
Parabola	${\displaystyle xx_{1}=2py+2py_{1}}$	${\displaystyle yy_{1}=2px+2px_{1}}$
Élips	${\displaystyle {\frac {xx_{1}}{b^{2}}}+{\frac {yy_{1}}{a^{2}}}=1}$	${\displaystyle {\frac {xx_{1}}{a^{2}}}+{\frac {yy_{1}}{b^{2}}}=1}$
Hiperbola	${\displaystyle {\frac {xx_{1}}{b^{2}}}-{\frac {yy_{1}}{a^{2}}}=1}$	${\displaystyle {\frac {xx_{1}}{a^{2}}}-{\frac {yy_{1}}{b^{2}}}=1}$
	Titik puseur (h,k)
Bunderan	${\displaystyle (x-h)(x_{1}-h)+(y-k)(y_{1}-k)=r^{2}}$ atawa ${\displaystyle xx_{1}+yy_{1}+{\frac {1}{2}}Ax+{\frac {1}{2}}Ax_{1}+{\frac {1}{2}}By+{\frac {1}{2}}By_{1}+C=0}$
Parabola	${\displaystyle (x-h)(x_{1}-h)=2p(y-k)+2p(y_{1}-k)}$	${\displaystyle (y-k)(y_{1}-k)=2p(x-h)+2p(x_{1}-h)}$
Élips	${\displaystyle {\frac {(x-h)(x_{1}-h)}{b^{2}}}+{\frac {(y-k)(y_{1}-k)}{a^{2}}}=1}$	${\displaystyle {\frac {(x-h)(x_{1}-h)}{a^{2}}}+{\frac {(y-k)(y_{1}-k)}{b^{2}}}=1}$
Hiperbola	${\displaystyle {\frac {(x-h)(x_{1}-h)}{b^{2}}}-{\frac {(y-k)(y_{1}-k)}{a^{2}}}=1}$	${\displaystyle {\frac {(x-h)(x_{1}-h)}{a^{2}}}-{\frac {(y-k)(y_{1}-k)}{b^{2}}}=1}$

Lamun titik ${\displaystyle (x_{1},y_{1})}$ nyampak di jero bentukna mangka aya 1 pasaruaan gurat toél (1 léngkah).

Lamun titik ${\displaystyle (x_{1},y_{1})}$ nyampak di luar bentukna mangka aya 2 pasaruaan gurat toél (2 léngkah).

Conto:

Titik puseur (0,0)

• Tangtukeun pasaruaan gurat toél anu ngagradién 2 kana ${\displaystyle y^{2}=16x}$!

jawab:

${\displaystyle y^{2}=16x->y^{2}=4(4x)jadip=4}$

${\displaystyle y=2x+{\frac {4}{2}}->y=2x+2}$

• Tangtukeun pasaruaan gurat toél anu ngaliwatan (4,8) kana ${\displaystyle y^{2}=16x}$!

jawab:

${\displaystyle y^{2}-16x=0mangkaasupkeun(4,8)(8)^{2}-16(4)=0=0}$ (jero)

ku cara bagi adil

${\displaystyle yy_{1}=2px+2px_{1}}$

${\displaystyle 8y=8x+8(4)}$

${\displaystyle 8y=8x+32}$ (dibagi 8)

${\displaystyle y=x+4}$

• Tangtukeun pasaruaan gurat toél anu ngaliwatan (1,5) kana ${\displaystyle y^{2}=16x}$!

jawab:

${\displaystyle y^{2}-16x=0mangkaasupkeun(1,5)(5)^{2}-16(1)=9>0}$ (luar)

ku cara bagi adil

${\displaystyle yy_{1}=2px+2px_{1}}$

${\displaystyle 5y=8x+8(1)}$

${\displaystyle 5y=8x+8}$

${\displaystyle y={\frac {8}{5}}x+{\frac {8}{5}}}$

asupkeun ${\displaystyle y^{2}=16x}$

${\displaystyle ({\frac {8}{5}}x+{\frac {8}{5}})^{2}=16x}$

${\displaystyle {\frac {64}{25}}x^{2}+{\frac {128}{25}}x+{\frac {64}{25}}-16x=0}$

${\displaystyle {\frac {64}{25}}x^{2}+{\frac {128}{25}}x+{\frac {64}{25}}-{\frac {400}{25}}x=0}$

${\displaystyle {\frac {64}{25}}x^{2}-{\frac {272}{25}}x+{\frac {64}{25}}=0}$ (dibagi 16/25)

${\displaystyle 4x^{2}-17x+4=0}$

mangka urang néangan niléy x

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

${\displaystyle x={\frac {17\pm {\sqrt {289-256}}}{8}}}$

${\displaystyle x={\frac {17\pm {\sqrt {33}}}{8}}}$

${\displaystyle x_{1}={\frac {17+{\sqrt {33}}}{8}}}$ atawa ${\displaystyle x_{2}={\frac {17-{\sqrt {33}}}{8}}}$

mangka urang néangan niléy y

pikeun ${\displaystyle x_{1}}$

${\displaystyle y_{1}={\frac {8}{5}}({\frac {17+{\sqrt {33}}}{8}})+{\frac {8}{5}}}$

${\displaystyle y_{1}={\frac {17}{5}}+{\frac {\sqrt {33}}{5}}+{\frac {8}{5}}}$

${\displaystyle y_{1}=5+{\frac {\sqrt {33}}{5}}}$

jadi ${\displaystyle ({\frac {17+{\sqrt {33}}}{8}},5+{\frac {\sqrt {33}}{5}})}$

pikeun ${\displaystyle x_{2}}$

${\displaystyle y_{2}={\frac {8}{5}}({\frac {17-{\sqrt {33}}}{8}})+{\frac {8}{5}}}$

${\displaystyle y_{2}={\frac {17}{5}}-{\frac {\sqrt {33}}{5}}+{\frac {8}{5}}}$

${\displaystyle y_{2}=5-{\frac {\sqrt {33}}{5}}}$

jadi ${\displaystyle ({\frac {17-{\sqrt {33}}}{8}},5-{\frac {\sqrt {33}}{5}})}$

balik deui ku cara bagi adil

pikeun pasaruaan toél kahiji

${\displaystyle yy_{1}=2px+2px_{1}}$

${\displaystyle (5+{\frac {\sqrt {33}}{5}})y=8x+8({\frac {17+{\sqrt {33}}}{8}})}$

${\displaystyle (5+{\frac {\sqrt {33}}{5}})y=8x+17+{\sqrt {33}}}$

pikeun pasaruaan toél kadua

${\displaystyle yy_{2}=2px+2px_{2}}$

${\displaystyle (5-{\frac {\sqrt {33}}{5}})y=8x+8({\frac {17-{\sqrt {33}}}{8}})}$

${\displaystyle (5-{\frac {\sqrt {33}}{5}})y=8x+17-{\sqrt {33}}}$

Titik puseur (h,k)

• Tangtukeun pasaruaan gurat toél ${\displaystyle y^{2}-6y-8x+9=0}$ ngaliwatan pasaruaan anu panceg lempeng ${\displaystyle y-2x-5=0}$!

jawab: robah jadi bentuk anu basajan

${\displaystyle y^{2}-6y-8x+9=0}$

${\displaystyle y^{2}-6y+9=8x}$

${\displaystyle (y-3)^{2}=8x}$

téangan gradién pasaruaan ${\displaystyle y-2x-5=0}$

${\displaystyle y-2x-5=0}$

${\displaystyle y=2x+5}$

gradién (${\displaystyle m_{1}}$) = 2 ku sabab panceg lempeng ngajadi ${\displaystyle m_{2}=-{\frac {1}{2}}}$

téang ${\displaystyle p}$

${\displaystyle (y-3)^{2}=8x->(y-3)^{2}=4(2x)jadip=2}$

${\displaystyle y=-{\frac {1}{2}}x+{\frac {2}{-{\frac {1}{2}}}}->y=-{\frac {1}{2}}x-4}$

• Tangtukeun pasaruaan gurat toél ${\displaystyle y^{2}-6y-8x+9=0}$ anu ordinatna 6!

jawab: robah jadi bentuk anu basajan

${\displaystyle y^{2}-6y-8x+9=0}$

${\displaystyle y^{2}-6y+9=8x}$

${\displaystyle (y-3)^{2}=8x}$

téangan absis anu mana ordinat 6

${\displaystyle (y-3)^{2}=8x}$

${\displaystyle (6-3)^{2}=8x}$

${\displaystyle 9=8x}$

${\displaystyle x={\frac {9}{8}}}$

ku cara bagi adil

${\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}$

${\displaystyle (y-3)(6-3)=4x+4({\frac {9}{8}})}$

${\displaystyle (y-3)3=4x+{\frac {9}{2}}}$

${\displaystyle 3y-9=4x+{\frac {9}{2}}}$

${\displaystyle 3y=4x+{\frac {27}{2}}}$

${\displaystyle y={\frac {4}{3}}x+{\frac {27}{6}}}$

• Tangtukeun pasaruaan gurat toél anu ngaliwatan (1,6) kana ${\displaystyle y^{2}-6y-8x+9=0}$!

robah jadi bentuk anu basajan

${\displaystyle y^{2}-6y-8x+9=0}$

${\displaystyle y^{2}-6y+9=8x}$

${\displaystyle (y-3)^{2}=8x}$

${\displaystyle (y-3)^{2}-8x=0mangkaasupkeun(1,6)(6-3)^{2}-8(1)=9-8=1>0}$ (luar)

ku cara bagi adil

${\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}$

${\displaystyle (y-3)(6-3)=4x+4(1)}$

${\displaystyle (y-3)3=4x+4}$

${\displaystyle 3y-9=4x+4}$

${\displaystyle 3y=4x+13}$

${\displaystyle y={\frac {4}{3}}x+{\frac {13}{3}}}$

mangka asupkeun ${\displaystyle (y-3)^{2}=8x}$

${\displaystyle ({\frac {4}{3}}x+{\frac {13}{3}}-3)^{2}=8x}$

${\displaystyle ({\frac {4}{3}}x+{\frac {4}{3}})^{2}=8x}$

${\displaystyle {\frac {16}{9}}x^{2}+{\frac {32}{9}}x+{\frac {16}{9}}-8x=0}$

${\displaystyle {\frac {16}{9}}x^{2}-{\frac {40}{9}}x+{\frac {16}{9}}=0}$ (dibagi 8/9)

${\displaystyle 2x^{2}+5x+2=0}$

mangka urang néangan niléy x

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

${\displaystyle x={\frac {5\pm {\sqrt {25-16}}}{4}}}$

${\displaystyle x={\frac {5\pm {\sqrt {9}}}{4}}}$

${\displaystyle x_{1}={\frac {5+{\sqrt {9}}}{4}}=2}$ atau ${\displaystyle x_{2}={\frac {5-{\sqrt {9}}}{4}}={\frac {1}{2}}}$

mangka urang néangan niléy y

pikeun ${\displaystyle x_{1}}$

${\displaystyle y_{1}={\frac {4}{3}}(2)+{\frac {13}{3}}={\frac {8}{3}}+{\frac {13}{3}}=7}$

jadi ${\displaystyle (2,7)}$

untuk ${\displaystyle x_{2}}$

${\displaystyle y_{2}={\frac {4}{3}}({\frac {1}{2}})+{\frac {13}{3}}={\frac {2}{3}}+{\frac {13}{3}}=5}$

jadi ${\displaystyle ({\frac {1}{2}},5)}$

balik deui ku cara bagi adil

pikeun pasaruaan toél kahiji

${\displaystyle (y-k)(y_{1}-k)=2px+2px_{1}}$

${\displaystyle (y-3)(7-3)=4x+4(2)}$

${\displaystyle (y-3)4=4x+8}$

${\displaystyle 4y-12=4x+8}$

${\displaystyle 4y=4x+20}$ (dibagi 4)

${\displaystyle y=x+5}$

pikeun pasaruaan toél kadua

${\displaystyle (y-k)(y_{2}-k)=2px+2px_{2}}$

${\displaystyle (y-3)(5-3)=4x+4({\frac {1}{2}})}$

${\displaystyle (y-3)2=4x+2}$

${\displaystyle 2y-6=4x+2}$

${\displaystyle 2y=4x+8}$ (dibagi 2)

${\displaystyle y=2x+4}$