Интеграл

Интеграл је један од најважнијих појмова математичке анализе. Постоји више врста интеграла, међу којима су најпознатији неодређени, одређени, Стилтјесов и други.

Одређени интеграл функције може се представити као обележена поља области ограничена графом функције.

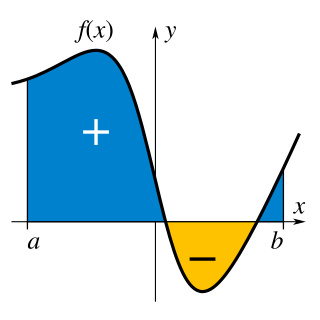
Неодређени интеграл се уводи као функција у извесном смислу инверзна диференцирању, односно као скуп свих примитивних функција за функцију која се интеграли. Одређени (или Риманов) интеграл се уводи помоћу тзв. интегралних сума. Иако је проучавање ових интеграла у почетку текло независно, чувена је формула која успоставља везу између њих - Њутн-Лајбницова формула.

Неодређени интеграл

Под неодређеним интегралом назива се скуп свих примитивних функција функције ${\displaystyle f(x)}$ и означава се са:

${\displaystyle \int f(x)\,dx,}$

где се ${\displaystyle f(x)}$ назива „подинтегралном функцијом (интеграндом)”, док је ${\displaystyle f(x)\,dx}$ „подинтегрални израз”.

Одређени интеграл

Збир површина нормалних одсечака приближава се траженој површини испод криве када ширина одсечака (на апсциси) тежи нули.

Да би се могао увести појам одређеног интеграла, пре свега је потребно увести појмове поделе сегмента, параметра поделе, скупа изабраних тачака поделе и Дарбуове суме.

Под поделом сегмента ${\displaystyle [a,b]}$ се сматра било који коначан непразан скуп са елементима ${\displaystyle x_{0},x_{1},...,x_{n}}$, где је ${\displaystyle x_{0}=a,x_{n}=b}$ и ${\displaystyle x_{i-1}<x_{i},i=1,...,n}$. Параметар ове поделе јесте ${\displaystyle max(x_{i}-x_{i-1})}$ за ${\displaystyle i=1,...,n}$. Скуп изабраних тачака ове поделе је скуп са елементима ${\displaystyle \xi _{1},\xi _{2},...,\xi _{n}}$ за које важи ${\displaystyle {x_{i-1}}\leq \xi _{i}\leq x_{i}}$ за све ${\displaystyle i=1,...,n}$. Дарбуова сума функције ${\displaystyle f}$ са датом поделом ${\displaystyle P}$ и скупом изабраних тачака ${\displaystyle \xi }$ је ${\displaystyle \sum _{i=1}^{n}f(\xi _{i})\cdot (x_{i}-x_{i-1})}$.

Сада је, по дефиницији, одређени интеграл функције ${\displaystyle f}$ на сегменту ${\displaystyle [a,b]}$ таква константа ${\displaystyle I}$ за коју важи

${\displaystyle (\forall \epsilon >0)(\exists \delta >0)(\forall P,\xi )\lambda (P)<\delta \implies |S(f,P,\xi )-I|<\epsilon }$,

где су ${\displaystyle P}$ — подела сегмента ${\displaystyle [a,b]}$, ${\displaystyle \xi }$ — скуп изабраних тачака поделе ${\displaystyle P}$, ${\displaystyle \lambda (P)}$ — параметар поделе ${\displaystyle P}$ и ${\displaystyle S(f,P,\xi )}$ — Дарбуова сума функције ${\displaystyle f}$ при подели ${\displaystyle P}$ и скупу изабраних тачака ${\displaystyle \xi }$. Тада се каже да је ${\displaystyle f}$ интеграбилна на ${\displaystyle [a,b]}$. Број ${\displaystyle I}$ који задовољава горенаведени критеријум се означава са

${\displaystyle \int _{a}^{b}f(x)dx}$.

Важно је назначити да немају све функције одређени интеграл на неком сегменту. Таква је Вајерштрасова функција која реалан број пресликава у 1 ако и само ако је рационалан и није 0, а иначе у 0. Испоставља се да је потребан и довољан услов да нека буде интеграбилна на неком сегменту њена прекидност у коначно много (или ни у једној) тачака тог сегмента.

Основна теорема интегралног рачуна

Основна теорема интегралног рачуна (која се често назива Њутн-Лајбницовом формулом) даје везу одређеног и неодређеног интеграла. Њом је доказано да се вредност одређеног интеграла може рачунати помоћу неодређеног интеграла (антидеривације) по формули:

${\displaystyle \int _{a}^{b}\!f(x)\,dx=F(b)-F(a)\,}$

где је примитивна функција (антидеривација) функције .

Методе интегрирања

За разлику од деривирања, интегрирање је знатно сложенији поступак. Док се познавањем таблице деривација елементарних функција и правила за деривирање (збира, разлике, производа, количника и сложене функције) може деривирати свака функцију, код интегрирања поступак није тако једноставан. Интегрирање познаје само два (елементарна) правила:

• Правило за интегрирање функције помножене скаларом

${\displaystyle \int A\cdot f(x)\,dx=A\cdot \int f(x)\,dx}$

• Правило за интегрирање збира и разлике функција

${\displaystyle \int (f(x)\pm g(x))\,dx=\int f(x)\,dx\pm \int g(x)\,dx}$

Не постоје правила за интегрирање производа, количника или сложене функције, а многи интеграли су доказано нерјешиви помоћу елементарних функција, попут интеграла ${\displaystyle \int e^{x^{2}}\,dx}$.

Три основне методе које се користе за решавање интеграла су^[1]:

• Метода непосредне интеграције је метода у којој је циљ да се подинтегрална функција запише на математички еквивалентан начин, који омогућава интегрирање помоћу таблице основних интеграла. На пример, не постоји правило за интегрирање умношка ${\displaystyle \int (x\cdot {\sqrt {x}})\,dx}$, али ако се подинтегрална функција запише свођењем израза на заједничку базу x, ${\displaystyle \int x^{\frac {3}{2}}\,dx}$, интеграл се решавамо уз помоћ таблице основних интеграла.
• Метода супституције је метода којом се део или цела подинтегрална функција замењује једноставнијим изразом.
• Метода парцијалне интеграције је метода чија је основна формула изведена из формуле за деривирање умношка. Смисао методе је, према поступку описаном формулом, део подинтегралне функције деривирати, а део интегрисати (отуда и назив парцијална интеграција). Циљ је да се добије једноставнији облик интеграла.

Неправи интеграл

Пример конвергентног неправог интеграла. Иако функција само тежи нули када се x повећава, скуп означен плавом бојом има површину једнаку неправом интегралу који износи 1.

Неправи интеграл је проширење концепта интеграла на полуотворене сегменте или на интервал ${\displaystyle (a,b)}$, с тим да рубна тачка може бити бесконачна и функција у околини тачке може бити неограничена.^[2]

Размотримо функцију ${\displaystyle x\mapsto e^{-x}}$. Помоћу неправог интеграла може се скупу испод графа те функције, и изнад осе x, на ${\displaystyle [0,+\infty )}$ доделити његова површина и то на овај начин:

${\displaystyle \int _{0}^{+\infty }e^{-x}dx=\lim _{B\to +\infty }\int _{0}^{B}e^{-x}dx.}$

У том случају написани лимес се назива неправим интегралом. Ако постоји тај лимес онда се каже да интеграл конвергира. Обично се у литератури неправи интеграл записује исто као и обичан интеграл, па читатељ треба испитивањем подинтегралне функције и граница интеграције да утврди о којем је интегралу реч.

Види још

• Неодређени интеграл
• Таблични интеграли
• Површински интеграл
• Запремински интеграл
• Списак интеграла рационалних функција
• Списак интеграла ирационалних функција
• Списак интеграла експоненцијалних функција
• Списак интеграла логаритамских функција
• Списак интеграла тригонометријских функција
• Списак интеграла хиперболичких функција
• Списак интеграла инверзних тригонометријских функција

Референце

1. „Tehnike integrisanja” (PDF). Архивирано из оригинала (PDF) 21. 09. 2013. г. Приступљено 22. 11. 2019.
2. Svetozar Kurepa: Matematička analiza 2 funkcije jedne varijable, Tehnička knjiga, Zagreb, 1971. (str. 231-234)

Литература

• Milton Abramowitz and Irene Stegun, editors. (1968). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.CS1 одржавање: Текст вишка: списак аутора (веза).
• I.S. Gradshteyn (И. С. Градштейн), I.M. Ryzhik (И. М. Рыжик); Alan Jeffrey, Daniel Zwillinger, editors. Table of Integrals, Series, and Products. ISBN 978-0-12-373637-6., seventh edition. Academic Press. 2007. . Errata. (Several previous editions as well.)
• A.P. Prudnikov (А. П. Прудников), Yu.A. Brychkov (Ю. А. Брычков), O.I. Marichev (О. И. Маричев). Integrals and Series. ISBN 978-2-88124-097-3.. First edition (Russian), volume 1–5, Nauka, 1981−1986. First edition (English, translated from the Russian by N.M. Queen), volume 1–5, Gordon & Breach Science Publishers/CRC Press, 1988–1992. . Second revised edition (Russian), volume 1–3, Fiziko-Matematicheskaya Literatura, 2003.
• Yu.A. Brychkov (Ю. А. Брычков). Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas. ISBN 978-1-58488-956-4.. Russian edition, Fiziko-Matematicheskaya Literatura, 2006. English edition, Chapman & Hall/CRC Press. 2008. .
• Daniel Zwillinger. CRC Standard Mathematical Tables and Formulae (31st изд.). ISBN 978-1-58488-291-6.. Chapman & Hall/CRC Press. 2002. . (Many earlier editions as well.)
• Hirsch, Meyer (1810). Integraltafeln: oder, Sammlung von Integralformeln. Duncker und Humblot.
• Hirsch, Meyer (1823). Integral Tables: Or, A Collection of Integral Fomulæ. W. Baynes & Son.
• David Bierens de Haan, Nouvelles Tables d'Intégrales définies (Engels, Leiden, 1862)
• Peirce, Benjamin Osgood (1800). A short table of integrals. Ginn & Company.
• Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd изд.). Wiley. ISBN 978-0-471-00005-1.
• Bourbaki, Nicolas (2004). Integration I. Springer Verlag. ISBN 978-3-540-41129-1.. In particular chapters III and IV.
• Burton, David M. (2005). The History of Mathematics: An Introduction (6th изд.). McGraw-Hill. стр. 359. ISBN 978-0-07-305189-5.
• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. стр. 247—252. ISBN 978-0-486-67766-8.
• Dahlquist, Germund; Björck, Åke (2008), „Chapter 5: Numerical Integration”, Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, Архивирано из оригинала 15. 6. 2007. г.
• Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications (1st изд.). John Wiley & Sons. ISBN 978-0-471-80958-6.
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, стр. §231
  Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, стр. 200—201
• Heath, T. L., ур. (2002). The Works of Archimedes. Dover. ISBN 978-0-486-42084-4.
  (Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H. (1953), „Integration in abstract spaces”, Bulletin of the American Mathematical Society, 59 (2): 111—139, ISSN 0273-0979, doi:10.1090/S0002-9904-1953-09694-X
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989). „Chapter 5: Numerical Quadrature”. Numerical Methods and Software. Prentice Hall. ISBN 978-0-13-627258-8.
• Kallio, Bruce Victor (1966), A History of the Definite Integral (PDF) (M.A. thesis), University of British Columbia, Архивирано из оригинала (PDF) 05. 03. 2014. г., Приступљено 22. 11. 2019
• Katz, Victor J. (2004). A History of Mathematics, Brief Version. Addison-Wesley. ISBN 978-0-321-16193-2.
• Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel, ур., Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
• Lieb, Elliott; Loss, Michael (2001), Analysis, Graduate Studies in Mathematics, 14 (2nd изд.), American Mathematical Society, ISBN 978-0821827833
• Miller, Jeff, Earliest Uses of Symbols of Calculus, Приступљено 22. 11. 2009
• O’Connor, J. J.; Robertson, E. F. (1996), A history of the calculus, Приступљено 9. 7. 2007
• Rudin, Walter (1987). „Chapter 1: Abstract Integration”. Real and Complex Analysis (International изд.). McGraw-Hill. ISBN 978-0-07-100276-9.
• Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised изд.), New York: Dover
• Shea, Marilyn (мај 2007), Biography of Zu Chongzhi, University of Maine, Архивирано из оригинала 14. 06. 2010. г., Приступљено 9. 1. 2009
• Siegmund-Schultze, Reinhard (2008), „Henri Lebesgue”, Ур.: Gowers, Timothy; June Barrow-Green; Leader, Imre, Princeton Companion to Mathematics, Princeton University Press.
• Stoer, Josef; Bulirsch, Roland (2002). „Topics in Integration”. Introduction to Numerical Analysis (3rd изд.). Springer. ISBN 978-0-387-95452-3..
• W3C (2006), Arabic mathematical notation
• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K. D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Johnson, William Woolsey (1909) Elementary Treatise on Integral Calculus, link from HathiTrust.
• Kowalk, W. P., Integration Theory Архивирано на сајту (27. фебруар 2012), University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P. S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) — a cookbook of definite integral techniques

Спољашње везе

• Теорија и задаци на
• Риманови редови - Интеграција функција (Џава симулација)
• Функција, извод и интеграл (Џава симулација)
• Интегратор Волфрам рисрча
• Калкулатор функција од WIMS
• Hazewinkel Michiel, ур. (2001). „Integral”. Encyclopaedia of Mathematics. Springer. 978-1556080104.