Diofantove jednačine

Diofantova jednačina je algebarska jednačina s dve ili više nepoznatih s celobrojnim koeficijentima u kojoj se traže celobrojna ili racionalna rešenja. Ime je dobila po Diofantu koji je prvi sistematski proučavao takve jednačine.^[1] Linearna Diofantova jednačina izjednačava zbir dva ili više monoma, svaki stepena 1 u jednoj od promenljivih, sa konstantom. Eksponencijalna Diofantova jednačina je ona u kojoj eksponenti na članovima mogu biti nepoznati.

Pronalaženje svih pravih trouglova sa celobrojnim dužinama stranica ekvivalentno je rešavanju Diofantove jednačine a² + b² = c².

Primeri

U sledećim Diofantovim jednačinama, w, x, y, i z su nepoznate, a ostalim slovima su date konstante:

ax + by = 1	Ovo je linearna Diofantova jednačina.
w3 + x3 = y3 + z3	Najmanje netrivijalno rešenje u pozitivnim celobrojnim brojevima je 123 + 13 = 93 + 103 = 1729. Poznato je po tome što mu je dato evidentno svojstvo 1729. godine, broj taksija (takođe nazvan Hardi–Ramanudžanov broj), po Ramanudžanu i Hardiju tokom sastanka 1917.[2] Postoji beskonačno mnogo netrivijalnih rešenja.[3]
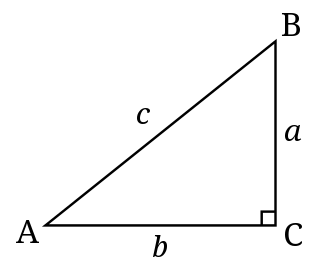
xn + yn = zn	Za n = 2 postoji beskonačno mnogo rešenja (x, y, z): Pitagorinih trojki. Za veće celobrojne vrednosti od n, poslednja Fermaova teorema (koju je inicijalno objavio Fermat 1637. i dokazao Endru Vajls 1995[4]) navodi da ne postoje pozitivna celobrojna rešenja (x, y, z).
x2 − ny2 = ±1	Ovo je Pelova jednačina, koja je dobila ime po engleskom matematičaru Džonu Pelu. Nju je studirao Bramagupta u 7. veku, kao i Fermat u 17. veku.
4/n = 1/x + 1/y + 1/z	Erdos-Štrausova hipoteza navodi da, za svaki pozitivni celi broj n ≥ 2, postoji rešenje u x, y, i z, sva od kojih su pozitivni celi brojevi. Iako se obično ne navodi u polinomnom obliku, ovaj primer je ekvivalentan polinomskoj jednačini 4xyz = yzn + xzn + xyn = n(yz + xz + xy).
x4 + y4 + z4 = w4	Ojler je pogrešno pretpostavio da nema netrivijalnih rešenja. Elkis je dokazao da ima beskonačno mnogo netrivijalnih rešenja, a Fraj je računarskom pretragom odredio najmanje netrivijalno rešenje.[5]

Linearne Diofantove jednačine

Diofantova linearna jednačina je jednačina oblika:

${\displaystyle ax+by=c}$

gdje su i neki celi brojevi.

Primer

${\displaystyle x=-{\frac {5}{3}}y}$

Kako je x ceo broj to je y deljivo sa 3

${\displaystyle y=3t}$

odnosno

${\displaystyle x=-5t}$

${\displaystyle (x,y)=(-5t,3t)}$

Teorema

Diofantova jednačina ${\displaystyle ax+by=c}$, gde su ${\displaystyle a}$,${\displaystyle b}$,${\displaystyle c}$ celi brojevi ${\displaystyle a^{2}+b^{2}\neq 0,}$ ima celobrojna rešenja ako i samo ako ${\displaystyle M(a,b)}$ deli ${\displaystyle c}$.

Ako su ${\displaystyle x_{0}}$ i ${\displaystyle y_{0}}$ rešenja te jednačine onda su sva rešenja oblika

${\displaystyle x=x_{0}+{\frac {b}{d}}t}$

${\displaystyle y=y_{0}+{\frac {a}{d}}t}$

Rešenje ${\displaystyle (x_{0},y_{0})}$ naziva se partikularno rešenje Diofantove jednačine. Opšte rešenje je zbir partikularnog rešenja i rešenja homogene jednačine ${\displaystyle ax+by=0}$

Primer

${\displaystyle 3x+5y=8}$

Partikularno rešenje je ${\displaystyle (1,1)}$, a rešenja pripadne homogene jednačine su ${\displaystyle (-5t,3t)}$, ${\displaystyle t\in Z}$

Rešenja jednačine su parovi ${\displaystyle (1-5t,1+3t)}$ za ${\displaystyle t\in Z}$ Za pronalaženje partikularnog rešenja Diofantove jednačine korististi se Euklidov algoritam pomoću kojeg određuju celi brojevi ${\displaystyle k}$ i ${\displaystyle l}$ za koje vredi ${\displaystyle ax+by=d}$, gde je ${\displaystyle d=M(a,b)}$, a zatim množenjem sa ${\displaystyle {\frac {c}{d}}}$ dobija se partikularno rešenje.

Primer

${\displaystyle 1000x-123y=5}$

${\displaystyle 1000=8*123+16}$

${\displaystyle 123=7*16+11}$

${\displaystyle 16=1*11+5}$

${\displaystyle 11=2*5+1}$

pa je

${\displaystyle 16=1000-8*123}$

${\displaystyle 11=123-7*16}$

${\displaystyle 5=16-1*11}$

${\displaystyle 1=11-2*5}$

U poslednju jednakost se uvrsti izraz za broj 5 iz pretposlednje jednakosti

${\displaystyle 1=11-2*5=11-2*(16-11*1)=3*11-2*16}$

${\displaystyle 1=3*(123-16*7)-2*16=3*123-23*16}$

${\displaystyle 1=3*123-23*(1000-8*123)=-23*1000+187*123}$

tj.

${\displaystyle 1=-23*1000+187*123}$ ${\displaystyle /*5}$

${\displaystyle 5=-115*1000+935*123}$

${\displaystyle x_{0}=-115}$

${\displaystyle y_{0}=-935}$

${\displaystyle x=123t}$

${\displaystyle y=1000t}$

Rešenje date jednadnačine je

${\displaystyle x=-115+123t}$

${\displaystyle y=-935+1000t}$ ${\displaystyle t\in Z}$

Primer

Za prevoz neke robe raspolaže se vrećama od 40 kg i 60 kg. Koliko treba uzeti jednih, a koliko drugih da se preveze 500 kg robe

Zadatak se može rešiti Ojlerovom metodom

${\displaystyle 40x+60y=500}$

${\displaystyle 2x+3y=25}$ za ${\displaystyle x\geq 0}$ i ${\displaystyle y\geq 0}$

${\displaystyle x={\frac {25-3y}{2}}=12-y+{\frac {1-y}{2}}}$

${\displaystyle {\frac {1-y}{2}}=u}$ ${\displaystyle u\ Z}$

${\displaystyle 2u+y=1}$

${\displaystyle y=1-2u}$

${\displaystyle x=12-(1-2u)+u=11+3u}$

Rešenja jednadčine su parovi ${\displaystyle (x,y}$) gde je ${\displaystyle x=11+3u}$ i ${\displaystyle y=1-2u}$

${\displaystyle -{\frac {11}{3}}\leq u\leq {\frac {1}{2}}=>u=-3,-2,-1,0}$

Traženi parovi ${\displaystyle (x,y}$) su ${\displaystyle (2,7)}$ ${\displaystyle (5,5)}$ ${\displaystyle (8,3)}$ i ${\displaystyle (11,1)}$

Nelinearne Diofantove jednačine

Ne postoji univerzalna metoda rešavanja ovih jednačina, ali zato postoji niz metoda kojima se rešavaju neki specijalni tipovi nelinearnih Diofantovih jednačina. Neki od tih metoda su:

1. metod faktorizacije
2. metod razlomka
3. metod poslednje cifre
4. metod kongruencije
5. metod zbira potencija s parnim eksponentima
6. metod nejednakosti

Metod faktorizacije

Metod faktorizacije sastoji se u tome da se jedna strana jednačine zapiše u obliku proizvoda celobrojnih vrednosti, pa uzimajući u obzir drugu stranu jednačine posmatraju se mogući slučajevi.

${\displaystyle xy+x-3y-3=0}$

(${\displaystyle x-3)(y+1)=3}$

Ovo je moguće za

x-3	y+1
1	3
-1	-3
3	1
-3	-1

odnosno

x	y
4	2
2	-4
6	0
0	-2

Metod razlomka

Osnovna ideja ovog metoda slična je kao kod metode faktorizacije, samo što se sada jedna stranu jednačine zapisuje u obliku razlomka dve celobrojne vrednosti, dok druga strane jednačine ima takođe celobrojnu vrednost. Zbog toga nazivnik tog razlomka mora deliti brojnik, što daje klasifikaciju mogućih slučajeva. Spomenuti razlomak se u praksi najčešće dobija tako da se jedna nepoznata izrazi kao racionalna funkcija druge.

${\displaystyle xy+2y=x}$

${\displaystyle y(x+2)=x}$

${\displaystyle y={\frac {x}{x+2}}=1-{\frac {2}{x+2}}}$

${\displaystyle x\ {\begin{Bmatrix}-1,-3,0,-4\end{Bmatrix}}}$

${\displaystyle y\ {\begin{Bmatrix}-1,3,0,-2\end{Bmatrix}}}$

Metod poslednje cifre

Metod poslednje cifre je podmetod metoda ostataka koji koristi ispitivanje ostataka pri deljenju brojem 10. Preciznije, razdvajanje slučajeva se vrši posmatranjem zadnje cifre nekih delova jednačine, te njihovim usklađivanjem.

${\displaystyle x^{2}+5y=199519941993}$

Kvadrat celog broja završava cifrom 0, 1, 4, 5, 6, ili 9, a broj ${\displaystyle 5y}$ sa 0 ili 5, pa zbir na levoj strani završava sa 0, 1, 4, 5, 6, ili 9, a ne sa 3. Jednačina nema rešenja.

Metod kongruencije

${\displaystyle x^{2}-4y=1995}$

${\displaystyle 1995}$ neparan, a ${\displaystyle 4y}$ paran, pa je ${\displaystyle x}$ neparan

${\displaystyle x=2k-1}$

${\displaystyle (2k-1)^{2}-4y=1995}$

${\displaystyle 4k^{2}-4k+1-4y=1995}$

${\displaystyle 4(k^{2}+k-y)=1994}$

Jednačina nema rešenja, jer 1994 nije deljivo sa 4

Metod zbira potencija s parnim eksponentima

Metod zbira je sličan metodu faktorizacije, samo što se sada jedna strana jednačine zapisuje u obliku zbira (najčešće nenegativnih) celih brojeva.

${\displaystyle x^{2}+y^{2}+2x-4y+8=0}$

${\displaystyle (x+1)^{2}+(y-2)^{2}=13}$

${\displaystyle (x+1)^{2}=9}$

${\displaystyle (y-2)^{2}=4}$

${\displaystyle (x,y)\in {\begin{Bmatrix}(1,5),(2,4)\end{Bmatrix}}}$

Metod nejednakosti

Ovaj metod se često koristi da bi se smanjio skup mogućih rešenja date jednačine, a zatim se na tom smanjenom skupu razlikuju slučajevi. Na tom smanjenom skupu razlikuju se slučajevi. Metod nejednakosti se često koristi i u kombinaciji s nekim drugom metodom za rešavanje nelinearnih Diofantovih jednačina

${\displaystyle 3^{x}+4^{x}=5^{x}}$

${\displaystyle x=2}$

${\displaystyle 3^{x}+4^{x}=5^{x}}$ ${\displaystyle /:5^{x}}$

${\displaystyle ({\frac {3}{5}})^{x}+({\frac {4}{5}})^{x}=1}$

za ${\displaystyle x<2}$

${\displaystyle ({\frac {3}{5}})^{x}+({\frac {4}{5}})^{x}>1}$

za ${\displaystyle x>2}$

${\displaystyle ({\frac {3}{5}})^{x}+({\frac {4}{5}})^{x}<1}$

Jednačina ima samo jedno rešenje ${\displaystyle x=2}$

Pelove i pelovske jednačine

Neka je zadata jednačina

${\displaystyle x^{2}+y^{2}=z^{2}}$

Uređena trojka (x,y,z) koja zadovoljava zadatu jednačinu se naziva Pitagorina trojka. Ako su brojevi x y z relativno prosti onda je to primitivna Pitagorina trojka

U svakoj primitivnoj Pitagorinoj trojci tačno je jedan od brojeva ${\displaystyle x}$,${\displaystyle y}$ neparan. Za ${\displaystyle x}$,${\displaystyle y}$ parne se ne bi radilo o primitivnoj Pitagorinoj trojci

Diofantova jednačina oblika

${\displaystyle x^{2}-dy^{2}=a}$ gde je ${\displaystyle d\in N}$ i nije potpun kvadrat je Pelova jednačina.

Pelova jednačina ima beskonačno mnogo rešenja u skupu prirodnih brojeva. Ako se pronađe najmanje (osnovno) rešenje ${\displaystyle (x_{e},y_{e})}$, preostala rešenja ${\displaystyle (x_{n},y_{n})}$ se mogu generisati na sledeće načine

1.  :${\displaystyle x_{n}+y_{n}{\sqrt {d}}}$ ${\displaystyle =(x_{n}+y_{n}{\sqrt {d}})^{n}}$
2.  :${\displaystyle x_{n+1}=2x_{n}x_{e}-x_{n-1}}$ i ${\displaystyle y_{n+1}=2x_{n}y_{e}-y_{n-1}}$ za ${\displaystyle (x_{0},y_{0})=(1,0)}$ i ${\displaystyle (x_{1},y_{1})=(x_{e},y_{e})}$
3.  :${\displaystyle x_{n+1}=x_{e}x_{n}+y_{e}dy_{n}}$ i ${\displaystyle y_{n+1}=x_{e}y_{n}+y_{e}dx_{n}}$

Jednačina

${\displaystyle x^{2}-dy^{2}=1}$ je Pelovska jednačina (jednačina Pelovog oblika)

Za razliku od Pelove jednačine ova jednačina nema uvek celobrojno rešenje.^[6]

Erdos–Štrausova hipoteza

Ovom hipotezom je pretpostavljeno da za sve prirodne brojeve ${\displaystyle n\geq 2}$ postoji racionalni broj ${\displaystyle 4/n}$ koji se može iskazati kao zbir tri jedinična razlomka s pozitivnim, celobrojnim nazivnicima kako sledi:

${\displaystyle {\frac {4}{n}}={\frac {1}{x}}+{\frac {1}{y}}+{\frac {1}{z}}.\,}$

Primer

za ${\displaystyle n=1801}$, postoji rešenje jednačine gde je ${\displaystyle x=451}$, ${\displaystyle y=295364}$ i ${\displaystyle z=3249004}$.

Pomnože li se obe strane jednačine sa ${\displaystyle nxyz}$, nalazi se Diofantova jednačina oblika:

${\displaystyle 4xyz=n(xy+xz+yz).\,}$ ^[7]

Reference

1. Mordell, L. J. (1969). Diophantine equations. Pure and Applied Mathematics. 30. Academic Press. ISBN 978-0-12-506250-3. Zbl 0188.34503.
2. „Quotations by Hardy”. Gap.dcs.st-and.ac.uk. Архивирано из оригинала 16. 7. 2012. г. Приступљено 20. 11. 2012.
3. Everest, G.; Ward, Thomas (2006), An Introduction to Number Theory, Graduate Texts in Mathematics, 232, Springer, стр. 117, ISBN 9781846280443.
4. Wiles, Andrew (1995). „Modular elliptic curves and Fermat's Last Theorem” (PDF). Annals of Mathematics. Annals of Mathematics. 141 (3): 443—551. JSTOR 2118559. OCLC 37032255. doi:10.2307/2118559. Архивирано из оригинала (PDF) 10. 07. 2023. г. Приступљено 06. 09. 2020.
5. Noam Elkies (1988). „On A⁴ + B⁴ + C⁴ = D⁴” (PDF). Mathematics of Computation. 51 (184): 825—835. JSTOR 2008781. MR 0930224. doi:10.2307/2008781.
6. „Diofantske jednadžbe / Pelove i pelovske jednadžbe” (PDF). Архивирано из оригинала (PDF) 8. 4. 2016. г. Приступљено 28. 12. 2018.
7. 4-parametrowa seria rozwiązań równania Erdősa-Strausa

Literatura

• Schmidt, Wolfgang M. (1991). Diophantine approximations and Diophantine equations. Lecture Notes in Mathematics. 1467. Berlin: Springer-Verlag. ISBN 978-3-540-54058-8. Zbl 0754.11020.
• Shorey, T. N.; Tijdeman, R. (1986). Exponential Diophantine equations. Cambridge Tracts in Mathematics. 87. Cambridge University Press. ISBN 978-0-521-26826-4. Zbl 0606.10011.
• Smart, Nigel P. (1998). The algorithmic resolution of Diophantine equations. London Mathematical Society Student Texts. 41. Cambridge University Press. ISBN 978-0-521-64156-2. Zbl 0907.11001.
• Stillwell, John (2004). Mathematics and its History (Second изд.). Springer Science + Business Media Inc. ISBN 978-0-387-95336-6.
• Dickson, Leonard Eugene (2005) [1920]. History of the Theory of Numbers. Volume II: Diophantine analysis. Mineola, NY: Dover Publications. ISBN 978-0-486-44233-4. MR 0245500. Zbl 1214.11002.
• Mordell, L. J. (1969). Diophantine equations. Pure and Applied Mathematics. 30. Academic Press. ISBN 0-12-506250-8. Zbl 0188.34503.
• Bashmakova, Izabella G. "Diophante et Fermat," Revue d'Histoire des Sciences 19 (1966), pp. 289–306
• Bashmakova, Izabella G. Diophantus and Diophantine Equations. Moscow: Nauka 1972 [in Russian]. German translation: Diophant und diophantische Gleichungen. Birkhauser, Basel/ Stuttgart, 1974. English translation: Diophantus and Diophantine Equations. Translated by Abe Shenitzer with the editorial assistance of Hardy Grant and updated by Joseph Silverman. The Dolciani Mathematical Expositions, 20. Mathematical Association of America, Washington, DC. 1997.
• Bashmakova, Izabella G. “Arithmetic of Algebraic Curves from Diophantus to Poincaré” Historia Mathematica 8 (1981), 393-416.
• Bashmakova, Izabella G., Slavutin, E.I. History of Diophantine Analysis from Diophantus to Fermat. Moscow: Nauka 1984 [in Russian].
• Bashmakova, Izabella G. “Diophantine Equations and the Evolution of Algebra,” American Mathematical Society Translations 147 (2), 1990, pp. 85–100. Translated by A. Shenitzer and H. Grant.
• Rashed, Roshdi, Houzel, Christian. Les Arithmétiques de Diophante : Lecture historique et mathématique, Berlin, New York : Walter de Gruyter, 2013.
• Rashed, Roshdi, Histoire de l’analyse diophantienne classique : D’Abū Kāmil à Fermat, Berlin, New York : Walter de Gruyter.

Spoljašnje veze

• .
• Hazewinkel Michiel, ур. (2001). „Diophantine equations”. Encyclopaedia of Mathematics. Springer. 978-1556080104.
• Diofantske jenačine Архивирано на сајту (11. јун 2012)