Риманова хипотеза

Риманова хипотеза је претпоставка о дистрибуцији нетривијалних нула Риманове зета-функције ${\displaystyle \zeta (s)\,}$. Први пут је формулисана у раду Бернарда Римана из 1859: О броју простих бројева испод задате величине ( ). Од тада, и поред огромних напора, овај проблем и даље остаје нерешен.

Реални део (у црвеној) и имагинарни део (у плавој боји) Риманове зета-функције на критичној линији Re(s) = 1/2. Првих неколико имагинарних нула се може видети за вредности Im(s) = ±14,135, ±21,022 и ±25,011.

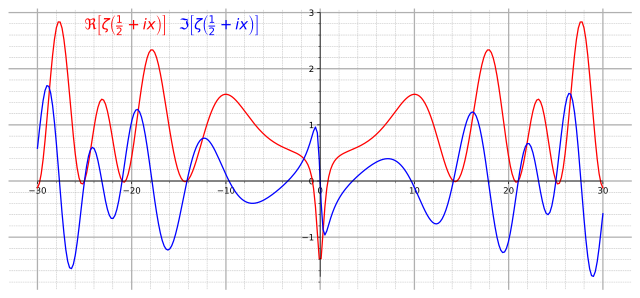
Риманова зета-функција је дефинисана за све комплексне бројеве ≠ 1, и има тривијалне нуле у парним негативним целим бројевима (). Риманова хипотеза каже да се све нетривијалне нуле налазе на једној правој у комплексној равни, конкретно:

Реални део било које нетривијалне нуле Риманове зета-функције је ½, односно све нетривијалне нуле се налазе на критичној линији ½ + .

Историјат

Рад из 1859. је Риманов једини оглед у теорији бројева, али је хипотеза изнета у њему један од најзначајнијих нерешених проблема у савременој математици, пре свега зато што се доста важних резултата ослања на важење ове хипотезе (рецимо у криптографији, факторизацији целих бројева и полинома).

Легенда каже да се копија сакупљених Риманових радова у Хурвицовој (енгл. ) библиотеци након његове смрти сама отварала на страни на којој се налазио исказ Риманове хипотезе.

Давид Хилберт је на Другом међународном конгресу математичара у Паризу, 8. августа 1900. године поставио проблем Риманове хипотезе као један од двадесеттри Хилбертова проблема (проблем број осам). За Хилберта је Риманова хипотеза имала посебан значај, када су га питали шта би најпре урадио након 500-годишњег сна, Хилберт је одговорио да би прво питао да ли је Риманова хипотеза доказана.

Годфри Харолд Харди (енгл. ) је 1914. године доказао да се на критичној линији ½ + налази бесконачно много нула.

Риманова хипотеза је један од седам Миленијумских проблема Математичког института Клеј.

Покушаји доказивања

Риманова хипотеза је као и Последња Фермаова теорема била инспирација за небројене покушаје доказивања, где су подједнако неуспешни били и врхунски и математичари аматери. Када је 1995. године енглески математичар Ендру Вајлс извео доказ Фермаове последње теореме - фокус математичке заједнице је преусмерен на Риманову хипотезу, најистакнутији нерешени проблем у математици данас. Овде су набројани значајни неуспешни покушаји у новом миленијуму.

Мати Питканен () у септембру 2001, повукао доказ због грешке у новембру исте године.^[1]

Карлос Кастро (), и Хорге Махеха () су у серији радова од 2001. до 2006. године пробали да изграде теорију (користећи суперсиметрије и квантномеханички приступ) која би омогућила доказивање Риманове хипотезе. Њихов приступ је одбачен.^[2]

Каида Ши () у јулу 2003. године, доказ садржавао грешку.^[3]

Луј д'Бранж () у јулу 2004. године, нађен контрапример.^[4] Аутор је касније објавио Извињење за доказ Риманове Хипотезе.^[5]

Јинжу Хан () у јуну 2007. године, доказ садржавао грешку.^[6]

Андреј Мадрецки () у јулу 2007. године, доказ садржавао грешку.^[7]

Лев Аизенберг () у децембру 2007. године, повукао доказ због грешке у јануару 2008. године.^[8]

Ксиан-Јин Ли () у јулу 2008. године, неколико дана касније је повукао доказ због грешке (на страни 29).^[9]

Мајкл Атија је предложио доказ Риманове хипотезе 2018. године.^[10]

Потрага за нулама Риманове зета-функције

Дуго се веровало да је Риманова хипотеза резултат дубоке интуиције и осећаја за проблем. Карл Лудвиг Сигел () је, међутим, у тридесетим годинама 20. века анализирајући Риманове рукописе пронашао рачун за првих неколико нула на критичној правој, на неколико децималних цифара тачности.

Риманова хипотеза је нумерички проверена за првих 10¹³ нула (за вредности на критичној линији до 2,4·10¹²). Овај резултат су 2004. године добили Ксавијер Гордон () и Патрик Демишел () користећи Одлизко-Шонаге () алгоритам^[11] из 1988. године.

Све познате вредности за нуле на критичној линији су по свему судећи ирационални бројеви.

Све познате нуле су првог реда. Иако постојење нула вишег реда не би оповргло Риманову хипотезу - изазвало би озбиљне проблеме за доста савремених рачунских техника.

Референце

1. „Мати Питканен (), Корак ближе доказу Риманове хипотезе”. arXiv:math/0109072 ., Приступљено 24. 4. 2013.
2. „Карлос Кастро () и Хорге Махеха (), Последњи кораци ка доказу Риманове хипотезе”. arXiv:hep-th/0208221 ., Приступљено 24. 4. 2013.
3. „Каида Ши (), Геометријски доказ уопштене Риманове хипотезе”. arXiv:math/0308001 ., Приступљено 24. 4. 2013.
4. „Луј д'Бранж (), Риманова зета-функција” (PDF). Приступљено 24. 4. 2013.
5. „Луј д'Бранж (), Извињење за доказ Риманове хипотезе” (PDF). Приступљено 24. 4. 2013.
6. „Јинжу Хан (), Истраживање осмог Хилбертовог проблема”. arXiv:0706.1929 ., Приступљено 24. 4. 2013.
7. „Андреј Мадрецки (), Кратак доказ Риманове хипотезе преко Брауновог кретања”. arXiv:0707.4196 ., Приступљено 24. 4. 2013.
8. „Лев Аизенберг (), Линделофова хипотеза је тачна док Риманова није”. arXiv:0801.0114 ., Приступљено 24. 4. 2013.
9. „Ксиан-Јин Ли (), Доказ Риманове Хипотезе”. arXiv:0807.0090 ., Приступљено 24. 4. 2013.
10. Британац решио математички проблем стар 160 година („Политика”, 24. септембар 2018)
11. Odlyzko, A. M.; Schönhage, A. (1988). „Fast Algorithms for Multiple Evaluations of the Riemann Zeta Function”. Transactions of the American Mathematical Society. 309 (2): 797—809. JSTOR 2000939. doi:10.1090/S0002-9947-1988-0961614-2.

Литература

• Artin, Emil (1924), „Quadratische Körper im Gebiete der höheren Kongruenzen. II. Analytischer Teil”, Mathematische Zeitschrift, 19 (1): 207—246, doi:10.1007/BF01181075
• Backlund, R. J. (1914), „Sur les Zéros de la Fonction ζ(s) de Riemann”, C. R. Acad. Sci. Paris, 158: 1979—1981
• Beurling, Arne (1955), „A closure problem related to the Riemann zeta-function”, Proceedings of the National Academy of Sciences of the United States of America, 41 (5): 312—314, Bibcode:1955PNAS...41..312B, MR 0070655, PMC 528084 , PMID 16589670, doi:10.1073/pnas.41.5.312
• Bohr, H.; Landau, E. (1914), „Ein Satz über Dirichletsche Reihen mit Anwendung auf die ζ-Funktion und die L-Funktionen”, Rendiconti del Circolo Matematico di Palermo, 37 (1): 269—272, doi:10.1007/BF03014823
• Bombieri, Enrico (2000), The Riemann Hypothesis – official problem description (PDF), Clay Mathematics Institute, Архивирано из оригинала (PDF) 22. 12. 2015. г., Приступљено 2008-10-25 Reprinted in Borwein et al. 2008.
• Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea, ур. (2008), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, ISBN 978-0-387-72125-5, doi:10.1007/978-0-387-72126-2
• Borwein, Peter; Ferguson, Ron; Mossinghoff, Michael J. (2008), „Sign changes in sums of the Liouville function”, Mathematics of Computation, 77 (263): 1681—1694, Bibcode:2008MaCom..77.1681B, MR 2398787, doi:10.1090/S0025-5718-08-02036-X 
• de Branges, Louis (1992), „The convergence of Euler products”, Journal of Functional Analysis, 107 (1): 122—210, MR 1165869, doi:10.1016/0022-1236(92)90103-P 
• Broughan, Kevin (2017), Equivalents of the Riemann Hypothesis, Cambridge University Press, ISBN 978-1108290784
• Burton, David M. (2006), Elementary Number Theory, Tata McGraw-Hill Publishing Company Limited, ISBN 978-0-07-061607-3
• Cartier, P. (1982), „Comment l'hypothèse de Riemann ne fut pas prouvée”, Seminar on Number Theory, Paris 1980–81 (Paris, 1980/1981), Progr. Math., 22, Boston, MA: Birkhäuser Boston, стр. 35—48, MR 693308
• Connes, Alain (1999), „Trace formula in noncommutative geometry and the zeros of the Riemann zeta function”, Selecta Mathematica. New Series, 5 (1): 29—106, MR 1694895, arXiv:math/9811068 , doi:10.1007/s000290050042
• Connes, Alain (2000), „Noncommutative geometry and the Riemann zeta function”, Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, стр. 35—54, MR 1754766
• Connes, Alain (2016), „An Essay on the Riemann Hypothesis”, Ур.: Nash, J. F.; Rassias, Michael, Open Problems in Mathematics, New York: Springer, стр. 225—257, arXiv:1509.05576 , doi:10.1007/978-3-319-32162-2_5
• Conrey, J. B. (1989), „More than two fifths of the zeros of the Riemann zeta function are on the critical line”, J. Reine Angew. Math., 1989 (399): 1—16, MR 1004130, doi:10.1515/crll.1989.399.1
• Conrey, J. Brian (2003), „The Riemann Hypothesis” (PDF), Notices of the American Mathematical Society: 341—353 Reprinted in Borwein et al. 2008.
• Conrey, J. B.; Li, Xian-Jin (2000), „A note on some positivity conditions related to zeta and L-functions”, International Mathematics Research Notices, 2000 (18): 929—940, MR 1792282, arXiv:math/9812166 , doi:10.1155/S1073792800000489
• Deligne, Pierre (1974), „La conjecture de Weil. I”, Publications Mathématiques de l'IHÉS, 43: 273—307, MR 0340258, doi:10.1007/BF02684373
• Deligne, Pierre (1980), „La conjecture de Weil : II”, Publications Mathématiques de l'IHÉS, 52: 137—252, doi:10.1007/BF02684780
• Deninger, Christopher (1998), „Some analogies between number theory and dynamical systems on foliated spaces”, Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), Documenta Mathematica, стр. 163—186, MR 1648030
• Dudek, Adrian W. (2014-08-21), „On the Riemann hypothesis and the difference between primes”, International Journal of Number Theory, 11 (3): 771—778, Bibcode:2014arXiv1402.6417D, ISSN 1793-0421, arXiv:1402.6417 , doi:10.1142/S1793042115500426
• Dyson, Freeman (2009), „Birds and frogs” (PDF), Notices of the American Mathematical Society, 56 (2): 212—223, MR 2483565
• Edwards, H. M. (1974), Riemann's Zeta Function, New York: Dover Publications, ISBN 978-0-486-41740-0, MR 0466039
• Fesenko, Ivan (2010), „Analysis on arithmetic schemes. II”, Journal of K-theory, 5 (3): 437—557, doi:10.1017/is010004028jkt103
• Ford, Kevin (2002), „Vinogradov's integral and bounds for the Riemann zeta function”, Proceedings of the London Mathematical Society, Third Series, 85 (3): 565—633, MR 1936814, arXiv:1910.08209 , doi:10.1112/S0024611502013655
• Franel, J.; Landau, E. (1924), „Les suites de Farey et le problème des nombres premiers" (Franel, 198–201); "Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel (Landau, 202–206)”, Göttinger Nachrichten: 198—206
• Ghosh, Amit (1983), „On the Riemann zeta function—mean value theorems and the distribution of |S(T)|”, J. Number Theory, 17: 93—102, doi:10.1016/0022-314X(83)90010-0 
• Gourdon, Xavier (2004), The 10¹³ first zeros of the Riemann Zeta function, and zeros computation at very large height (PDF)
• Gram, J. P. (1903), „Note sur les zéros de la fonction ζ(s) de Riemann” (PDF), Acta Mathematica, 27: 289—304, doi:10.1007/BF02421310
• Hadamard, Jacques (1896), „Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques”, Bulletin de la Société Mathématique de France, 14: 199—220, doi:10.24033/bsmf.545  Reprinted in Borwein et al. 2008.
• Hardy, G. H. (1914), „Sur les Zéros de la Fonction ζ(s) de Riemann”, C. R. Acad. Sci. Paris, 158: 1012—1014, JFM 45.0716.04 Reprinted in Borwein et al. 2008.
• Hardy, G. H.; Littlewood, J. E. (1921), „The zeros of Riemann's zeta-function on the critical line”, Math. Z., 10 (3–4): 283—317, doi:10.1007/BF01211614
• Haselgrove, C. B. (1958), „A disproof of a conjecture of Pólya”, Mathematika, 5 (2): 141—145, ISSN 0025-5793, MR 0104638, Zbl 0085.27102, doi:10.1112/S0025579300001480 Reprinted in Borwein et al. 2008.
• Haselgrove, C. B.; Miller, J. C. P. (1960), Tables of the Riemann zeta function, Royal Society Mathematical Tables, Vol. 6, Cambridge University Press, ISBN 978-0-521-06152-0, MR 0117905 Review
• Hutchinson, J. I. (1925), „On the Roots of the Riemann Zeta-Function”, Transactions of the American Mathematical Society, 27 (1): 49—60, JSTOR 1989163, doi:10.2307/1989163 
• Ingham, A.E. (1932), The Distribution of Prime Numbers, Cambridge Tracts in Mathematics and Mathematical Physics, 30, Cambridge University Press. Reprinted (1990) 978-0-521-39789-6, MR1074573
• Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (Second edition), New York: Springer, ISBN 0-387-97329-X
• Ivić, A. (1985), The Riemann Zeta Function, New York: John Wiley & Sons, ISBN 978-0-471-80634-9, MR 0792089 (Reprinted by Dover 2003)
• Ivić, Aleksandar (2008), „On some reasons for doubting the Riemann hypothesis”, Ур.: Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea, The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, стр. 131—160, ISBN 978-0-387-72125-5, arXiv:math.NT/0311162 
• Karatsuba, A. A. (1984a), „Zeros of the function ζ(s) on short intervals of the critical line”, Izv. Akad. Nauk SSSR, Ser. Mat. (на језику: руски), 48 (3): 569—584, MR 0747251
• Karatsuba, A. A. (1984b), „Distribution of zeros of the function ζ(1/2 + it)”, Izv. Akad. Nauk SSSR, Ser. Mat. (на језику: руски), 48 (6): 1214—1224, MR 0772113
• Karatsuba, A. A. (1985), „Zeros of the Riemann zeta-function on the critical line”, Trudy Mat. Inst. Steklov. (на језику: руски) (167): 167—178, MR 0804073
• Karatsuba, A. A. (1992), „On the number of zeros of the Riemann zeta-function lying in almost all short intervals of the critical line”, Izv. Ross. Akad. Nauk, Ser. Mat. (на језику: руски), 56 (2): 372—397, Bibcode:1993IzMat..40..353K, MR 1180378, doi:10.1070/IM1993v040n02ABEH002168
• Karatsuba, A. A.; Voronin, S. M. (1992), The Riemann zeta-function, de Gruyter Expositions in Mathematics, 5, Berlin: Walter de Gruyter & Co., ISBN 978-3-11-013170-3, MR 1183467, doi:10.1515/9783110886146
• Keating, Jonathan P.; Snaith, N. C. (2000), „Random matrix theory and ζ(1/2 + it)”, Communications in Mathematical Physics, 214 (1): 57—89, Bibcode:2000CMaPh.214...57K, MR 1794265, doi:10.1007/s002200000261
• Knauf, Andreas (1999), „Number theory, dynamical systems and statistical mechanics”, Reviews in Mathematical Physics. A Journal for Both Review and Original Research Papers in the Field of Mathematical Physics, 11 (8): 1027—1060, Bibcode:1999RvMaP..11.1027K, MR 1714352, doi:10.1142/S0129055X99000325
• von Koch, Niels Helge (1901), „Sur la distribution des nombres premiers”, Acta Mathematica, 24: 159—182, doi:10.1007/BF02403071
• Kurokawa, Nobushige (1992), „Multiple zeta functions: an example”, Zeta functions in geometry (Tokyo, 1990), Adv. Stud. Pure Math., 21, Tokyo: Kinokuniya, стр. 219—226, MR 1210791
• Lapidus, Michel L. (2008), In search of the Riemann zeros, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4222-5, MR 2375028, doi:10.1090/mbk/051
• Шаблон:Eom
• Lehmer, D. H. (1956), „Extended computation of the Riemann zeta-function”, Mathematika. A Journal of Pure and Applied Mathematics, 3 (2): 102—108, MR 0086083, doi:10.1112/S0025579300001753
• Leichtnam, Eric (2005), „An invitation to Deninger's work on arithmetic zeta functions”, Geometry, spectral theory, groups, and dynamics, Contemp. Math., 387, Providence, RI: Amer. Math. Soc., стр. 201—236, MR 2180209, doi:10.1090/conm/387/07243.
• Levinson, N. (1974), „More than one-third of the zeros of Riemann's zeta function are on σ = 1/2”, Adv. Math., 13 (4): 383—436, MR 0564081, doi:10.1016/0001-8708(74)90074-7
• Littlewood, J. E. (1962), „The Riemann hypothesis”, The scientist speculates: an anthology of partly baked idea, New York: Basic books
• van de Lune, J.; te Riele, H. J. J.; Winter, D. T. (1986), „On the zeros of the Riemann zeta function in the critical strip. IV”, Mathematics of Computation, 46 (174): 667—681, JSTOR 2008005, MR 829637, doi:10.2307/2008005 
• Massias, J.-P.; Nicolas, Jean-Louis; Robin, G. (1988), „Évaluation asymptotique de l'ordre maximum d'un élément du groupe symétrique”, Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica, 50 (3): 221—242, MR 960551, doi:10.4064/aa-50-3-221-242 
• Mazur, Barry; Stein, William (2015), Prime Numbers and the Riemann Hypothesis
• Montgomery, Hugh L. (1973), „The pair correlation of zeros of the zeta function”, Analytic number theory, Proc. Sympos. Pure Math., XXIV, Providence, R.I.: American Mathematical Society, стр. 181—193, MR 0337821 Reprinted in Borwein et al. 2008.
• Montgomery, Hugh L. (1983), „Zeros of approximations to the zeta function”, Ур.: Erdős, Paul, Studies in pure mathematics. To the memory of Paul Turán, Basel, Boston, Berlin: Birkhäuser, стр. 497—506, ISBN 978-3-7643-1288-6, MR 820245
• Montgomery, Hugh L.; Vaughan, Robert C. (2007), Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, 97, Cambridge University Press, ISBN 978-0-521-84903-6
• Nicely, Thomas R. (1999), „New maximal prime gaps and first occurrences”, Mathematics of Computation, 68 (227): 1311—1315, Bibcode:1999MaCom..68.1311N, MR 1627813, doi:10.1090/S0025-5718-99-01065-0 , Архивирано из оригинала 30. 12. 2014. г., Приступљено 25. 07. 2020.
• Nyman, Bertil (1950), On the One-Dimensional Translation Group and Semi-Group in Certain Function Spaces, PhD Thesis, University of Uppsala: University of Uppsala, MR 0036444
• Odlyzko, A. M.; te Riele, H. J. J. (1985), „Disproof of the Mertens conjecture”, Journal für die reine und angewandte Mathematik, 1985 (357): 138—160, MR 783538, doi:10.1515/crll.1985.357.138, Архивирано из оригинала 2012-07-11. г.
• Odlyzko, A. M. (1987), „On the distribution of spacings between zeros of the zeta function”, Mathematics of Computation, 48 (177): 273—308, JSTOR 2007890, MR 866115, doi:10.2307/2007890 
• Odlyzko, A. M. (1990), „Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results”, Séminaire de Théorie des Nombres de Bordeaux, Série 2, 2 (1): 119—141, MR 1061762, doi:10.5802/jtnb.22 
• Odlyzko, A. M. (1992), The 10²⁰-th zero of the Riemann zeta function and 175 million of its neighbors (PDF) This unpublished book describes the implementation of the algorithm and discusses the results in detail.
• Odlyzko, A. M. (1998), The 10²¹st zero of the Riemann zeta function (PDF)
• Ono, Ken; Soundararajan, K. (1997), „Ramanujan's ternary quadratic form”, Inventiones Mathematicae, 130 (3): 415—454, Bibcode:1997InMat.130..415O, doi:10.1007/s002220050191
• Patterson, S. J. (1988), An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics, 14, Cambridge University Press, ISBN 978-0-521-33535-5, MR 933558, doi:10.1017/CBO9780511623707
• Platt, David; Trudgian, Tim (2020), The Riemann hypothesis is true up to ${\displaystyle 3\cdot 10^{12}}$, arXiv:2004.09765v1 
• Radziejewski, Maciej (2007), „Independence of Hecke zeta functions of finite order over normal fields”, Transactions of the American Mathematical Society, 359 (5): 2383—2394, MR 2276625, doi:10.1090/S0002-9947-06-04078-5 , „There are infinitely many nonisomorphic algebraic number fields whose Dedekind zeta functions have infinitely many nontrivial multiple zeros.”
• Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5
• Riemann, Bernhard (1859), „Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse”, Monatsberichte der Berliner Akademie. In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953). Original manuscript (with English translation). Reprinted in Borwein et al. 2008 and Edwards 1974
• Riesel, Hans; Göhl, Gunnar (1970), „Some calculations related to Riemann's prime number formula”, Mathematics of Computation, 24 (112): 969—983, JSTOR 2004630, MR 0277489, doi:10.2307/2004630
• Riesz, M. (1916), „Sur l'hypothèse de Riemann”, Acta Mathematica, 40: 185—190, doi:10.1007/BF02418544 
• Robin, G. (1984), „Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann”, Journal de Mathématiques Pures et Appliquées, Neuvième Série, 63 (2): 187—213, MR 774171
• Rosser, J. Barkley; Yohe, J. M.; Schoenfeld, Lowell (1969), „Rigorous computation and the zeros of the Riemann zeta-function. (With discussion)”, Information Processing 68 (Proc. IFIP Congress, Edinburgh, 1968), Vol. 1: Mathematics, Software, Amsterdam: North-Holland, стр. 70—76, MR 0258245
• Rudin, Walter (1973), Functional Analysis, 1st edition (January 1973), New York: McGraw-Hill, ISBN 0-070-54225-2
• Salem, Raphaël (1953), „Sur une proposition équivalente à l'hypothèse de Riemann”, Les Comptes rendus de l'Académie des sciences, 236: 1127—1128, MR 0053148
• Sarnak, Peter (2005), Problems of the Millennium: The Riemann Hypothesis (2004) (PDF), Clay Mathematics Institute, Приступљено 2015-07-28 Reprinted in Borwein et al. 2008.
• Schoenfeld, Lowell (1976), „Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II”, Mathematics of Computation, 30 (134): 337—360, JSTOR 2005976, MR 0457374, doi:10.2307/2005976
• Schumayer, Daniel; Hutchinson, David A. W. (2011), „Physics of the Riemann Hypothesis”, Reviews of Modern Physics, 83 (2): 307—330, Bibcode:2011RvMP...83..307S, arXiv:1101.3116 , doi:10.1103/RevModPhys.83.307
• Selberg, Atle (1942), „On the zeros of Riemann's zeta-function”, SKR. Norske Vid. Akad. Oslo I., 10: 59 pp, MR 0010712
• Selberg, Atle (1946), „Contributions to the theory of the Riemann zeta-function”, Arch. Math. Naturvid., 48 (5): 89—155, MR 0020594
• Selberg, Atle (1956), „Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series”, J. Indian Math. Soc. (N.S.), 20: 47—87, MR 0088511
• Serre, Jean-Pierre (1969—1970), „Facteurs locaux des fonctions zeta des varietés algébriques (définitions et conjectures)”, Séminaire Delange-Pisot-Poitou, 19
• Sheats, Jeffrey T. (1998), „The Riemann hypothesis for the Goss zeta function for F_q[T]”, Journal of Number Theory, 71 (1): 121—157, MR 1630979, arXiv:math/9801158 , doi:10.1006/jnth.1998.2232
• Siegel, C. L. (1932), „Über Riemanns Nachlaß zur analytischen Zahlentheorie”, Quellen Studien zur Geschichte der Math. Astron. Und Phys. Abt. B: Studien 2: 45—80 Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.
• Speiser, Andreas (1934), „Geometrisches zur Riemannschen Zetafunktion”, Mathematische Annalen, 110: 514—521, JFM 60.0272.04, doi:10.1007/BF01448042, Архивирано из оригинала 2015-06-27. г.
• Spira, Robert (1968), „Zeros of sections of the zeta function. II”, Mathematics of Computation, 22 (101): 163—173, JSTOR 2004774, MR 0228456, doi:10.2307/2004774 
• Stein, William; Mazur, Barry (2007), What is Riemann's Hypothesis? (PDF), Архивирано из оригинала (PDF) 2009-03-27. г.
• Suzuki, Masatoshi (2011), „Positivity of certain functions associated with analysis on elliptic surfaces”, Journal of Number Theory, 131 (10): 1770—1796, doi:10.1016/j.jnt.2011.03.007 
• Titchmarsh, Edward Charles (1935), „The Zeros of the Riemann Zeta-Function”, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, The Royal Society, 151 (873): 234—255, Bibcode:1935RSPSA.151..234T, JSTOR 96545, doi:10.1098/rspa.1935.0146 
• Titchmarsh, Edward Charles (1936), „The Zeros of the Riemann Zeta-Function”, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, The Royal Society, 157 (891): 261—263, Bibcode:1936RSPSA.157..261T, JSTOR 96692, doi:10.1098/rspa.1936.0192 
• Titchmarsh, Edward Charles (1986), The theory of the Riemann zeta-function (2nd изд.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853369-6, MR 882550
• Trudgian, Timothy (2011), „On the success and failure of Gram's Law and the Rosser Rule”, Acta Arithmetica, 125 (3): 225—256, doi:10.4064/aa148-3-2
• Turán, Paul (1948), „On some approximative Dirichlet-polynomials in the theory of the zeta-function of Riemann”, Danske Vid. Selsk. Mat.-Fys. Medd., 24 (17): 36, MR 0027305 Reprinted in Borwein et al. 2008.
• Turing, Alan M. (1953), „Some calculations of the Riemann zeta-function”, Proceedings of the London Mathematical Society, Third Series, 3: 99—117, MR 0055785, doi:10.1112/plms/s3-3.1.99
• de la Vallée-Poussin, Ch.J. (1896), „Recherches analytiques sur la théorie des nombers premiers”, Ann. Soc. Sci. Bruxelles, 20: 183—256
• de la Vallée-Poussin, Ch.J. (1899—1900), „Sur la fonction ζ(s) de Riemann et la nombre des nombres premiers inférieurs à une limite donnée”, Mem. Couronnes Acad. Sci. Belg., 59 (1) Reprinted in Borwein et al. 2008.
• Weil, André (1948), Sur les courbes algébriques et les variétés qui s'en déduisent, Actualités Sci. Ind., no. 1041 = Publ. Inst. Math. Univ. Strasbourg 7 (1945), Hermann et Cie., Paris, MR 0027151
• Weil, André (1949), „Numbers of solutions of equations in finite fields”, Bulletin of the American Mathematical Society, 55 (5): 497—508, MR 0029393, doi:10.1090/S0002-9904-1949-09219-4  Reprinted in Oeuvres Scientifiques/Collected Papers by Andre Weil 0-387-90330-5
• Weinberger, Peter J. (1973), „On Euclidean rings of algebraic integers”, Analytic number theory ( St. Louis Univ., 1972), Proc. Sympos. Pure Math., 24, Providence, R.I.: Amer. Math. Soc., стр. 321—332, MR 0337902
• Wiles, Andrew (2000), „Twenty years of number theory”, Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, стр. 329—342, ISBN 978-0-8218-2697-3, MR 1754786
• Zagier, Don (1977), „The first 50 million prime numbers” (PDF), Math. Intelligencer, Springer, 0: 7—19, MR 643810, doi:10.1007/BF03039306, Архивирано из оригинала (PDF) 2009-03-27. г.
• Zagier, Don (1981), „Eisenstein series and the Riemann zeta function”, Automorphic forms, representation theory and arithmetic (Bombay, 1979), Tata Inst. Fund. Res. Studies in Math., 10, Tata Inst. Fundamental Res., Bombay, стр. 275—301, MR 633666
• Sabbagh, Karl (2003a), The greatest unsolved problem in mathematics, Farrar, Straus and Giroux, New York, ISBN 978-0-374-25007-2, MR 1979664
• Sabbagh, Karl (2003b), Dr. Riemann's zeros, Atlantic Books, London, ISBN 978-1-843-54101-1
• du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, MR 2060134
• Rockmore, Dan (2005), Stalking the Riemann hypothesis, Pantheon Books, ISBN 978-0-375-42136-5, MR 2269393
• Derbyshire, John (2003), Prime Obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, MR 1968857
• Watkins, Matthew (2015), Mystery of the Prime Numbers, Liberalis Books, ISBN 978-1782797814, MR 0000000
• Frenkel, Edward (2014), The Riemann Hypothesis Numberphile, Mar 11, 2014 (video)

Спољашње везе

• Миленијумски проблеми Математичког Института Клеј (), (2000), објава награде од милион долара за решење Миленијумских проблема.
• Фототипија рукописа Римановог рада из 1859. године Архивирано на сајту (18. август 2014), у којем се први пут помиње Риманова хипотеза.
• , текст посвећен Римановој хипотези на сајту .
• Apostol, Tom, Where are the zeros of zeta of s?
• Borwein, Peter, The Riemann Hypothesis (PDF), Архивирано из оригинала (PDF) 2009-03-27. г.
• Conrad, K. (2010), Consequences of the Riemann hypothesis
• Conrey, J. Brian; Farmer, David W, Equivalences to the Riemann hypothesis, Архивирано из оригинала 2010-03-16. г.
• Gourdon, Xavier; Sebah, Pascal (2004), Computation of zeros of the Zeta function
• Odlyzko, Andrew, Home page
• Odlyzko, Andrew (2002), Zeros of the Riemann zeta function: Conjectures and computations (PDF) Slides of a talk
• Pegg, Ed (2004), Ten Trillion Zeta Zeros, Math Games website.
• Pugh, Glen, Java applet for plotting Z(t)
• Rubinstein, Michael, algorithm for generating the zeros, Архивирано из оригинала 2007-04-27. г..
• du Sautoy, Marcus (2006), Prime Numbers Get Hitched, Seed Magazine, Архивирано из оригинала 2017-09-22. г., Приступљено 2006-03-27
• Stein, William A., What is Riemann's hypothesis, Архивирано из оригинала 2009-01-04. г.
• de Vries, Andreas (2004), The Graph of the Riemann Zeta function ζ(s), a simple animated Java applet.
• Watkins, Matthew R. (2007-07-18), Proposed proofs of the Riemann Hypothesis