Експоненцијална функција

Експоненцијална функција је једна од најважнијих функција у математици. Она има облик ${\displaystyle f(x)=ab^{x},}$, где је b позитивни реални број, и у коме се аргумент x јавља као експонент. За реалне бројеве c и d, функција облика ${\displaystyle f(x)=ab^{cx+d}}$ је исто тако експоненцијална функција, јер се може написати као ${\displaystyle ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}}$. Осим ако није другачије назначено, термин се генерално односи на функцију позитивне вредности реалне променљиве, иако се може проширити на комплексне бројеве или генерализовати на друге математичке објекте као што су матрице или Лијеве алгебре. Експоненцијална функција је настала из појма експоненцијације (поновљено множење), али модерне дефиниције (постоји неколико еквивалентних карактеризација) дозвољавају да се ригорозно прошири на све реалне аргументе, укључујући ирационалне бројеве. Њена свеприсутна појава у чистој и примењеној математици навела је математичара Валтера Рудина на мишљење да је експоненцијална функција „најважнија функција у математици“.^[1][2]

Експоненцијална функција је скоро равна (споро се пење) за негативне вредности x, а онда брзо расте за позитивне вредности x.

Експоненцијалне функције са базама 2 и 1/2

Као функције реалне променљиве, експоненцијалне функције су јединствено окарактерисане чињеницом да је брзина раста такве функције (тј. њеног деривата) директно пропорционална вредности функције. Константа пропорционалности овог односа је природни логаритам базе b:

${\displaystyle {\frac {d}{dx}}b^{x}=b^{x}\log _{e}b.}$

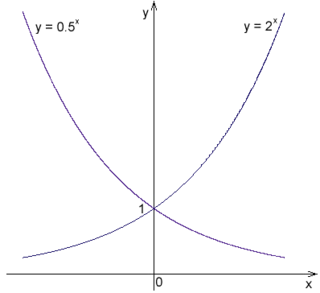
За b = 1 реална експоненцијална функција је константа и њен извод је нула, јер је ${\displaystyle \log _{e}b=0,}$ за позитивно a и b > 1 реалне експоненцијалне функције су монотоно растуће (као што је приказано за b = e и b = 2), јер је извод већи од нуле за све аргументе, и за b < 1 оне су монотоно опадајуће (као што је приказано за b = 1/2), јер је извод мањи од нуле за све аргументе.

Природна експоненцијална функција се означава се као () или , при чему је e = 2.71828..., што је заправо Неперова константа, основа природног логаритма. Извод ове функције је она сама:

${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\log _{e}e=e^{x}.}$

Експоненцијална функција је реална функција једне променљиве, дефинисана за све реалне бројеве, која је увек позитивна и растућа. Никада не додирује -осу, мада јој је -оса једина асимптота. Њена инверзна функција, природни логаритам, је дефинисана само за позитивне вредности променљиве .

Будући да промена базе експоненцијалне функције само доводи до појаве додатног константног фактора, рачунски је погодно редуковати проучавање експоненцијалних функција у математичкој анализи на проучавање ове одређене функције, конвенционално зване „природна експоненцијална функција”,^[3][4] или једноставно, „експоненцијална функција” и означава се са

${\displaystyle x\mapsto e^{x}}$ or ${\displaystyle x\mapsto \exp(x).}$

Док су обе ознаке уобичајене, прва нотација се обично користи за једноставније експоненте, док се друга ознака обично користи када је експонент компликован израз.

Експоненцијална функција задовољава фундаментални идентитет множења

${\displaystyle e^{x+y}=e^{x}e^{y},}$ for all ${\displaystyle x,y\in \mathbb {R} .}$

Овај идентитет обухвата комплексне експонената. Може се показати да је свако континуирано, ненулто решење функцијске једначине ${\displaystyle f(x+y)=f(x)f(y)}$ експоненцијална функција, ${\displaystyle f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto b^{x},}$ with ${\displaystyle b>0.}$ Фундаментални мултипликативни идентитет, заједно са дефиницијом e као e¹, показује да је ${\displaystyle e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ terms}}}}$ за природне бројеве n и повезује експоненцијалну функцију са елементарним појмом експоненцијације. Аргумент експоненцијалне функције може бити било који реални или комплексни број или потпуно другачија врста математичког објекта (на пример, матрица).

Њена свеприсутна појава у чистој и примењеној математици навела је математичара В. Рудина на мишљење да је експоненцијална функција „најважнија функција у математици”.^[1] У примењеним ситуацијама, експоненцијалне функције моделују однос у којем константна промена у независној променљивој даје исту пропорционалну промену (тј. процентуално повећање или смањење) у зависној променљивој. Ово је широко заступљено у природним и друштвеним наукама; стога се експоненцијална функција појављује у мноштву различитих контекста унутар физике, хемије, инжењерства, математичке биологије и економије.

Графикон функције ${\displaystyle y=e^{x}}$ је нагнут нагоре, и повећава се брже са порастом x. Графикон увек лежи изнад x-осе, али може бити произвољно близу негативног x; стога је x-оса хоризонтална асимптота. Нагиб тангенте на графикону у свакој тачки једнак је њеној y-координати у тој тачки, као што следи из њене функције извода (види горе). Њена инверзна функција је природни логаритам, означен са ${\displaystyle \log ,}$^[5] ${\displaystyle \ln ,}$^[6] или ${\displaystyle \log _{e};}$ због тога, неки стари текстови^[7] наводе експоненцијалну функцију као антилогаритам.

Формална дефиниција

Главни чланак: Карактеристике експоненцијалне функције

Експоненцијална функција (у плавом), и сума првих n + 1 чланова њене серија (у црвеном).

Експоненцијална функција може се дефинисати на доста еквивалентних начина, преко бесконачних редова. Одређеније, може се дефинисати преко степених редова:^[1]

${\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }$

У овим дефиницијама, ${\displaystyle n!}$ означава факторијел броја , а је или произвољан реалан број, комплексан број, елемент Банахове алгебре (на пример, квадратна матрица). Пошто је радијус конвергенције ових степених редова бесконачан, ова дефиниција је заправо применљива на све комплексне бројеве ${\displaystyle z\in \mathbb {C} }$ (погледајте доле за проширење ${\displaystyle \exp(x)}$ на комплексну раван). Константа e се тада може дефинисати као ${\textstyle e=\exp(1)=\sum _{k=0}^{\infty }(1/k!).}$

Диференцијација члан по члан овог степеног реда показује да је ${\displaystyle (d/dx)(\exp x)=\exp x}$ за свако реално x, што доводи до још једне заједничке карактеризације ${\displaystyle \exp(x)}$ као јединственог решења диференцијалне једначине

${\displaystyle y'(x)=y(x),}$

задовољавајући иницијални услов ${\displaystyle y(0)=1.}$

На основу ове карактеризације, правило ланца^[8][9] показује да њена инверзна функција, природни логаритам, задовољава ${\displaystyle (d/dy)(\log _{e}y)=1/y}$ за ${\displaystyle y>0,}$ или ${\textstyle \log _{e}y=\int _{1}^{y}{\frac {1}{t}}\,dt.}$ Ова релација доводи до мање уобичајене дефиниције реалне експоненцијалне функције${\displaystyle \exp(x)}$ као решења по ${\displaystyle y}$ једначине

${\displaystyle x=\int _{1}^{y}{\frac {1}{t}}\,dt.}$

Помоћу биномне теореме и дефиниције степеног реда, експоненцијална функција се такође може дефинисати као следећи лимит:^[10]

${\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$

Својства

Употребом природног логаритма, може се дефинисати нешто генералнија експоненцијална функција. Функција

${\displaystyle \!\,a^{x}=e^{x\ln a}}$

дефинисана за свако > 0, и за сваки реалан број се назива експоненцијална функција за основу .

Приметимо да горња једнакост важи за = , пошто је

${\displaystyle \!\,e^{x\ln e}=e^{x\left(1\right)}=e^{x}.}$

Експоненцијалне функције „сједињују“ сабирање и множење, што се види следећим експоненцијалним законима:

${\displaystyle \!\,a^{0}=1}$

${\displaystyle \!\,a^{1}=a}$

${\displaystyle \!\,a^{x+y}=a^{x}a^{y}}$

${\displaystyle \!\,a^{xy}=\left(a^{x}\right)^{y}}$

${\displaystyle \!\,{1 \over a^{x}}=\left({1 \over a}\right)^{x}=a^{-x}}$

${\displaystyle \!\,a^{x}b^{x}=(ab)^{x}}$

Горње важи за све позитивне реалне бројеве и , и за све реалне бројеве и . Изрази који укључују разломке и кореновање често могу бити упрошћени коришћењем експоненцијалне нотације јер:

${\displaystyle {1 \over a}=a^{-1}}$

и, за свако > 0, реалан број , и цео број  > 1:

${\displaystyle {\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}}$

За сваку реалну константу важи:

${\displaystyle f'(0)=\lim _{h\to 0}{\frac {e^{ch}-1}{h}}=c}$

за ${\displaystyle f(x)=e^{ch}}$

Изводи и диференцијалне једначине

Значај експоненцијалне функције у математици и науци уопште углавном потиче од својстава њеног извода. Конкретније,

${\displaystyle {d \over dx}e^{x}=e^{x}}$

Види се да је извод самом себи, што је јединствено својство међу свим реалним функцијама. Други начини да се каже исто ово укључују:

• Нагиб графика експоненцијалне функције у било којој тачки једнак је вредности функције у тој тачки.
• Стопа пораста експоненцијалне функције у тачки једнака је вредности функције у тој тачки.
• Експоненцијална функција је решење диференцијалне једначине ${\displaystyle y'=y}$.

Заправо, огроман број диференцијалних једначина има решење у експоненцијалним функцијама, укључујући Шредингерову једначину и Лапласову једначину, као и једначине простог хармонијског кретања.

За експоненцијалне функције осталих основа важи:

${\displaystyle {d \over dx}a^{x}=(\ln a)a^{x}}$

Према томе, свака експоненцијална функција је константни умножак сопственог извода.

Уколико је раст или опадање променљиве пропорционално њеној величини – као у случају неограниченог раста становништва, радиоактивног распада, сложене камате – онда се та променљива може писати као константа помножена експоненцијалном функцијом времена.

Даље, за било коју диференцијабилну функцију () важи:

${\displaystyle {d \over dx}e^{f(x)}=f'(x)e^{f(x)}}$

Нумеричка вредност

Да бисмо добили нумеричку вредност експоненцијалне функције, бесконачни ред можемо написати као:

${\displaystyle e^{x}={1 \over 0!}+x\,\left({1 \over 1!}+x\,\left({1 \over 2!}+x\,\left({1 \over 3!}+\cdots \right)\right)\right)}$

${\displaystyle =1+{x \over 1}\left(1+{x \over 2}\left(1+{x \over 3}\left(1+\cdots \right)\right)\right)}$

Овај израз брзо конвергира уколико је мање од 1.

Да бисмо ово остварили, можемо искористити следећу једнакост.

${\displaystyle e^{x}\,}$	${\displaystyle =e^{z+f}\,}$
	${\displaystyle =e^{z}\times \left[{1 \over 0!}+f\,\left({1 \over 1!}+f\,\left({1 \over 2!}+f\,\left({1 \over 3!}+\cdots \right)\right)\right)\right]}$

• где је ${\displaystyle z}$ цео део од ${\displaystyle x}$
• где је ${\displaystyle f}$ део иза покретног зареза од ${\displaystyle x}$
• следи, ${\displaystyle f}$ је увек мање од 1 и збир ${\displaystyle f}$ и ${\displaystyle z}$ даје ${\displaystyle x}$.

Вредност константе се може претходно израчунато множећи самим собом пута.

На комплексној равни

Када се посматра као функција комплексне променљиве, експоненцијална функција задржава своја битна својства:

${\displaystyle \!\,e^{z+w}=e^{z}e^{w}}$

${\displaystyle \!\,e^{0}=1}$

${\displaystyle \!\,e^{z}\neq 0}$

${\displaystyle \!\,{d \over dz}e^{z}=e^{z}}$

за свако и .

Оваква експоненцијална функција је холоморфна, са имагинарном периодом ${\displaystyle 2\pi i}$ и може се написати и као:

${\displaystyle \!\,e^{a+bi}=e^{a}(\cos b+i\sin b)}$

где су и реални бројеви. Ова формула повезује експоненцијалну функцију са тригонометријским функцијама и хиперболичким функцијама. Овим се види да се све елементарне функције осим полиномијалних потомци експоненцијалне функције у једном или другом смислу.

Погледајте и Ојлерову формулу.

Матрице и Банахова алгебра

Дефиниција експоненцијалне функције дата изнад може се користити и за сваку Банахову алгебру, и одређеније за квадратне матрице. У овом случају имамо:

${\displaystyle \ e^{x+y}=e^{x}e^{y}{\mbox{ if }}xy=yx}$

${\displaystyle \ e^{0}=1}$

${\displaystyle \ e^{x}}$ има инверз и он је ${\displaystyle \ e^{-x}}$

извод ${\displaystyle \ e^{x}}$ у тачки ${\displaystyle \ x}$ је она матрица која пресликава ${\displaystyle \ u}$ у ${\displaystyle \ ue^{x}}$.

Референце

1. Rudin, Walter (1987). Real and complex analysis (3rd изд.). New York: McGraw-Hill. стр. 1. ISBN 978-0-07-054234-1.
2. Weisstein, Eric W. „Exponential Function”. mathworld.wolfram.com (на језику: енглески). Приступљено 2020-08-28.
3. Goldstein, Lay; Schneider, Asmar (2006). Brief calculus and its applications (11th изд.). Prentice–Hall. ISBN 978-0-13-191965-5.
4. Courant; Robbins (1996). Stewart, ур. What is Mathematics? An Elementary Approach to Ideas and Methods (2nd revised изд.). Oxford University Press. стр. 448. ISBN 978-0-13-191965-5. „This natural exponential function is identical with its derivative. This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…”
5. In pure mathematics, the notation log x generally refers to the natural logarithm of x or a logarithm in general if the base is immaterial.
6. The notation ln x is the ISO standard and is prevalent in the natural sciences and secondary education (US). However, some mathematicians (e.g., Paul Halmos) have criticized this notation and prefer to use log x for the natural logarithm of x.
7. Converse; Durrell (1911). Plane and spherical trigonometry. C. E. Merrill Co. стр. 12. „Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm) ...”
8. Rodríguez, Omar Hernández; López Fernández, Jorge M. (2010). „A Semiotic Reflection on the Didactics of the Chain Rule”. The Mathematics Enthusiast. 7 (2): 321—332. S2CID 29739148. doi:10.54870/1551-3440.1191 . Приступљено 2019-08-04.
9. Rodríguez, Omar Hernández; López Fernández, Jorge M. (2010). „A Semiotic Reflection on the Didactics of the Chain Rule”. The Mathematics Enthusiast. 7 (2): 321—332. S2CID 29739148. doi:10.54870/1551-3440.1191 . Приступљено 2019-08-04.
10. Eli Maor, e: the Story of a Number, p.156.

Литература

• Walter Rudin, Principles of Mathematical Analysis, 3rd edition (McGraw–Hill, 1976), chapter 8.
• Edwin Hewitt and Karl Stromberg, (1965). Real and Abstract Analysis. Springer..

Спољашње везе

• Hazewinkel Michiel, ур. (2001). „Exponential function”. Encyclopaedia of Mathematics. Springer. 978-1556080104.
• „Complex exponential function”. PlanetMath.
• „Derivative of exponential function”. PlanetMath.
• Weisstein, Eric W. „Exponential Function”. MathWorld.