V geometriji in kristalogarfiji je Bravaisova mreža neskončen niz točk, ki jih generira niz diskretnih translacijskih operacij, zapisanih z enačbo:
- R = n1a1 + n2a2 + n3a3
ni so poljubna cela števila, ai pa osnovni vektorji, ki ležijo na različnih ravninah in povezujejo mrežo. Mreža je v katerem koli položaju vektorja R popolnoma enaka.
Mreže so dobile ime po njihovem avtorju, francoskemu fiziku in mineralogu Augustu Bravaisu.[1]
Kristal je zgrajen iz istovrstnih ali raznovrstnih atomov, ki se ponavljajo v vsaki mrežni točki. Kristal, gledan iz katere koli mrežne točke, izgleda popolnoma enako.
Bravaisovi mreži se pogosto obravnavata kot ekvivalentni, če imata izomorfno simetrijsko grup. V tridimenzionalnem prostoru je v tem smislu možnih 14 Bravaisovih mrež. 14 možnih simetrijskih grup Bravaisovih mrež je 14 od 230 prostorskih grup.
V 0-dimenzionalnem in 1-dimenzionalnem prostoru sta samo po ena Bravaisova mreža. V 2-dimenzionalnem prostoru je pet Bravaisovih mrež: poševna, pravokotna, centrirano pravokotna, heksagonalna in kvadratna.[2]
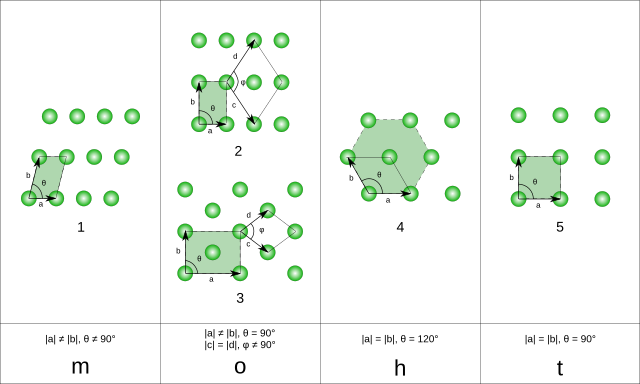
V treh dimenzijah je 14 Bravaisovih mrež, ki nastanejo s kombiniranjem sedmih mrežnih (aksialnih) sistemov s centriranji mreže.
Mreža ima lahko naslednja centriranja:
- enostavno centriranje (P): mrežne točke so samo na ogliščih osnovne celice
- telesno centriranje (I): dodatna mrežna točka je v središču celice
- ploskovno centriranje (F): po ena dodatna mrežna točka je v središču vsake ploskve celice
- centriranje na samo eni ploskvi (centriranje A, B ali C): dodatna mrežna točka je v središču ene od ploskev celice
Za opis mrež niso potrebne vse kombinacije kristalnih sistemov in centriranj. Celotno število možnih kombinacij je 7 × 6 = 42, vendar je med njimi nekaj takih, ki so enakovredne. Monoklinsko mrežo I se na primer lahko z drugačno izbiro kristalnih osi opiše kot monoklinsko mrežo C. Na podoben način se vse A- ali B-centrirane mreže lahko opišejo s centriranjem C- ali P-. Število kombinacij se zato zmanjša na 14 Bravaisovih mrež, ki so prikazane v naslednji preglednici.
| 7 mrežnih sistemov | 14 Bravaisovih mrež | |||
| Triklinski | P | |||
 | ||||
| Monoklinski | P | C | ||
 |
 | |||
| Ortorombski | P | C | I | F |
 |
 |
 |
 | |
| Tetragonalni | P | I | ||
 |
 | |||
| Romboedrični |
P | |||
 | ||||
| Heksagonalni | P | |||
 | ||||
| Kubični |
P | I | F | |
 |
 |
 | ||
Volomen osnovne celice se izračuna z enačbo a • b × c, pri čemer so a, b in c mrežni vektorji. Bravaisove mreže imajo naslednje volumne:
| Mrežni sistem | Enačba za izračun prostornine | |||
| Triklinski | ||||
| Monoklinski | ||||
| Ortorombski | ||||
| Tetragonalni | ||||
| Romboedrični | ||||
| Heksagonalni | ||||
| Kubični | ||||
V štirih dimenzijah je 52 Bravaisovih mrež. 21 mrež je osnovnih, 31 pa centriranih.[3]
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.






