Hypercube

In geometry, a hypercube is a kind of polytope. It is an analogue of a square (n = 2) or a cube (n = 3) in another number of dimensions (which is known as n-dimensional). A hypercube is a closed, compact, convex figure that is made of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.

Perspective projections

Cube (3-cube)	Tesseract (4-cube)

An n-dimensional hypercube is also called an n-cube or an n-dimensional cube. The term "measure polytope" is also used, notably in the work of H. S. M. Coxeter (originally from Elte, 1912),^[1] but it has been superseded.

The hypercube is the special case of a hyperrectangle (also called an n-orthotope), where all of its parts are equal.

A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2ⁿ points in Rⁿ with each coordinate equal to 0 or 1 is called "the" unit hypercube. A unit hypercube's longest diagonal in n dimension is equal to ${\displaystyle {\sqrt {n}}}$.

Construction

A diagram showing how to create a tesseract from a point.

An animation showing how to create a tesseract from a point.

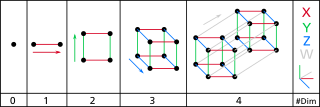
A hypercube can be made by making a copy of the last hypercube and moving it into the next dimension, then connecting the two objects. They are as follows:

0 – A point is a hypercube of dimension zero.

1 – If one moves a copy of the point by one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one.

2 – If one moves a copy of this line segment in a perpendicular direction from itself; it sweeps out a 2-dimensional square.

3 – If one moves a copy of the square by one unit length in the direction perpendicular to the plane it lies on, it will make a 3-dimensional cube.

4 – If one moves a copy of the cube by one unit length into the fourth dimension, it makes a 4-dimensional unit hypercube (a unit tesseract).

This can be done in any number of dimensions. This process of sweeping out the polytopes can be formalized mathematically as a Minkowski sum: the d-dimensional hypercube is the Minkowski sum of d mutually perpendicular unit-length line segments, and is therefore an example of a zonotope.

The 1-skeleton of a hypercube is a hypercube graph.

Related pages

• Simplex - the n-dimensional analogue of the triangle
• Hyperrectangle - the general case of the hypercube, where the base is a rectangle.