Уравнение Сакура — Тетроде

Уравнение Сакура — Тетроде или формула Сакура — Тетроде описывает энтропию одноатомного идеального газа^[1].

Он назван в честь Хьюго Мартина Тетроде^[2] (1895—1931) и Отто Сакура^[3] (1880—1914), которые разработали его независимо как решение газовой статистики Больцмана и уравнений энтропии примерно 1912 году^[4].

Формула

Уравнение Сакура — Тетроде выражает энтропию ${\displaystyle S}$ одноатомного идеального газа с точки зрения его термодинамического состояния, в частности, его объёма ${\displaystyle V}$, внутренней энергии ${\displaystyle U}$, и числа частиц ${\displaystyle N}$^[1]:

${\displaystyle {\frac {S}{k_{\rm {B}}N}}=\ln \left[{\frac {V}{N}}\left({\frac {4\pi m}{3h^{2}}}{\frac {U}{N}}\right)^{3/2}\right]+{\frac {5}{2}},}$

где ${\displaystyle k_{\mathrm {B} }}$ — постоянная Больцмана, ${\displaystyle m}$ — масса частицы газа и ${\displaystyle h}$ — постоянная Планка.

Уравнение также можно выразить через тепловую длину волны ${\displaystyle \Lambda }$:

${\displaystyle {\frac {S}{k_{\rm {B}}N}}=\ln \left({\frac {V}{N\Lambda ^{3}}}\right)+{\frac {5}{2}},}$

Функциональные зависимости энтропии от температуры классических и квантовых идеальных газов (ферми-газ, бозе-газ) в трёх измерениях. Хотя все они находятся в близком согласии при высоких температурах, они расходятся при низких температурах, когда классическая энтропия (уравнение Сакура — Тетроде) начинает приближаться к отрицательным значениям.

Вывод уравнения Сакура — Тетроде см. в парадоксе Гиббса. Об ограничениях, налагаемых на энтропию идеального газа только термодинамикой, см. Статью об идеальном газе.

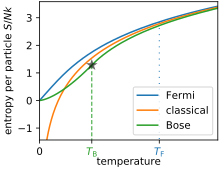
Приведённые выше выражения предполагают, что газ находится в классическом режиме и описывается статистикой Максвелла — Больцмана (с «правильным счётом Больцмана»). Из определения тепловой длины волны это означает, что уравнение Сакура — Тетроде справедливо только тогда, когда

${\displaystyle {\frac {V}{N\Lambda ^{3}}}\gg 1.}$

Энтропия, предсказываемая уравнением Сакура — Тетроде, стремится к отрицательной бесконечности, когда температура приближается к нулю.

Константа Сакура — Тетрода

Константа Сакура — Тетрода, обозначаемая S₀/R, равна S/k_BN, оцененная при температуре T = 1 К, при стандартном давлении (100 кПа или 101,325 кПа), на один моль идеального газа, состоящего из частиц с массой, равной атомной постоянной массы. Рекомендуемое значение CODATA 2018 года:

S ₀ / R = −1,15170753706 ± (45) для p ^o = 100 кПа^[5]

S ₀ / R = −1,16487052358 ± (45) для p ^o = 101,325 кПа.^[6]

Теоретико-информационная интерпретация

В дополнение к термодинамическму взгляду на энтропию, инструменты теории информации могут быть использованы для рассмотрения информационной энтропии. В частности, можно вывести уравнение Сакура — Тетроде в терминах теории информации. Общая энтропия представлена как сумма четырёх отдельных энтропий, то есть четырёх различных источников недостающей информации. Это позиционная неопределённость, неопределённость импульса, квантовомеханический принцип неопределённости и неразличимость частиц^[7]. Суммируя четыре части, уравнение Сакура — Тетрода задаётся следующим образом:

${\displaystyle {\begin{aligned}{\frac {S}{k_{\rm {B}}N}}&=[\ln V]+\left[{\frac {3}{2}}\ln \left(2\pi emk_{\rm {B}}T\right)\right]+[-3\ln h]+\left[-{\frac {\ln N!}{N}}\right]\\&\approx \ln \left[{\frac {V}{N}}\left({\frac {2\pi mk_{\rm {B}}T}{h^{2}}}\right)^{\frac {3}{2}}\right]+{\frac {5}{2}}\end{aligned}}}$

При выводе используется приближение Стирлинга: ${\displaystyle \ln N!\approx N\ln N-N}$. Строго говоря, использование размерных аргументов для логарифмов неверно, однако их использование представляет собой «сокращение», созданное для простоты. Если бы каждый логарифмический аргумент был разделён на неопределённую стандартную величину, выраженную через неопределённую стандартную массу, длину и время, ир эти стандартные значения сократились бы в конечном результате, что привело бы к тому же выводу. Отдельные члены энтропии не будут абсолютными, а скорее будут зависеть от выбранных стандартов и будут отличаться для разных стандартов на аддитивную величину.

Примечания

1. Schroeder, Daniel V. (1999), An Introduction to Thermal Physics, Addison Wesley Longman, ISBN 0-201-38027-7
2. H. Tetrode (1912) «Die chemische Konstante der Gase und das elementare Wirkungsquantum» (The chemical constant of gases and the elementary quantum of action), Annalen der Physik 38: 434—442. See also: H. Tetrode (1912) "Berichtigung zu meiner Arbeit: «Die chemische Konstante der Gase und das elementare Wirkungsquantum» " Архивная копия от 6 января 2018 на Wayback Machine (Correction to my work: «The chemical constant of gases and the elementary quantum of action»), Annalen der Physik 39: 255—256.
3. Сакур опубликовал свои выводы в следующей серии статей:

   1. O. Sackur (1911) «Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme» (The application of the kinetic theory of gases to chemical problems), Annalen der Physik, 36: 958—980.
   2. O. Sackur, «Die Bedeutung des elementaren Wirkungsquantums für die Gastheorie und die Berechnung der chemischen Konstanten» (The significance of the elementary quantum of action to gas theory and the calculation of the chemical constant), Festschrift W. Nernst zu seinem 25jährigen Doktorjubiläum gewidmet von seinen Schülern (Halle an der Saale, Germany: Wilhelm Knapp, 1912), pages 405—423.
   3. O. Sackur (1913) «Die universelle Bedeutung des sog. elementaren Wirkungsquantums» (The universal significance of the so-called elementary quantum of action), Annalen der Physik 40: 67-86.
4. Grimus, Walter (2013). "100th anniversary of the Sackur–Tetrode equation". Annalen der Physik. 525 (3): A32—A35. arXiv:1112.3748. Bibcode:2013AnP...525A..32G. doi:10.1002/andp.201300720. ISSN 0003-3804.
5. 2018 CODATA Value: Sackur–Tetrode constant  (неопр.). The NIST Reference on Constants, Units, and Uncertainty. NIST (20 мая 2019). Дата обращения: 20 мая 2019. Архивировано 29 июня 2019 года.
6. 2018 CODATA Value: Sackur–Tetrode constant  (неопр.). The NIST Reference on Constants, Units, and Uncertainty. NIST (20 мая 2019). Дата обращения: 20 мая 2019. Архивировано 29 июня 2019 года.
7. Ben-Naim, Arieh (2008), A Farewell to Entropy: Statistical Thermodynamics Based on Information, World Scientific, ISBN 978-981-270-706-2, Дата обращения: 12 декабря 2017.