Loading AI tools
область математики Из Википедии, свободной энциклопедии
Прикладна́я матема́тика — область математики, рассматривающая применение математических методов, алгоритмов в других областях науки и техники. Примерами такого применения будут: численные методы, математическая физика, линейное программирование, оптимизация и исследование операций, моделирование сплошных сред (Механика сплошных сред), биоматематика и биоинформатика, теория информации, теория игр, теория вероятностей и статистика, финансовая математика и актуарные расчёты, криптография, а следовательно комбинаторика и в некоторой степени конечная геометрия, теория графов в приложении к сетевому планированию, и во многом то, что называется информатикой. В вопросе о том, что является прикладной математикой, нельзя составить чёткую логическую классификацию. Математические методы обычно применяются к специфическому классу прикладных задач путём составления математической модели.
| Наука | |
| Прикладная математика | |
|---|---|
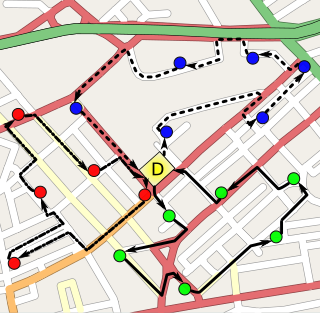
По ироническому утверждению В. И. Арнольда, разница между чистой и прикладной математикой не научная, а социальная и заключается в том, что чистому математику платят за открытие математических фактов, в то время как прикладному математику платят за решение практических задач. Арнольд также замечает, что в России почти каждый математик сочетал «чистую» и «прикладную» математику.

Исторически, прикладная математика состояла в основном из прикладного анализа, прежде всего теории дифференциальных уравнений; теории приближений (в широком смысле, включающей асимптотические методы, вариационные методы и численный анализ); и прикладная теория вероятностей. Эти области математики имели непосредственное отношение к развитию ньютоновской физики, и различие между математиками и физиками не было чётко выражено до середины XIX века. Это оставило педагогический след в Соединённых Штатах Америки: до начала XX века такие предметы, как классическая механика, часто преподавались на факультетах прикладной математики в американских университетах, а не на факультетах физики, а механику жидкости всё ещё преподают на факультетах прикладной математики. В настоящее время финансовая математика преподаётся на математических факультетах в университетах, и считается разделом прикладной математики[1]. Инженерные и компьютерные факультеты традиционно применяют прикладную математику.

Сегодня термин «прикладная математика» используется в более широком смысле. Он включает в себя классические области, отмеченные выше, а также другие области, которые становятся всё более важными в приложениях. Даже такие области, как теория чисел, которая является частью чистой математики, ныне важны в приложениях (таких как криптография), хотя они, как правило, не считаются частью прикладной математики как таковой. Иногда термин «применимая математика» используется для различия между традиционной прикладной математикой, которая развивалась наряду с физикой, и многими областями математики, которые применимы к современным задачам в современном мире.
Нет единого мнения о том, что представляют собой различные разделы прикладной математики. Классификация затрудняется из-за того, что математика и наука меняются со временем, а также из-за того, что университеты организуют кафедры, курсы и степени. Логическая классификация прикладной математики больше основана на социологии специалистов, использующих математику, чем на вопросе определения точного характера математики.
Многие математики проводят различие между «прикладной математикой», которая связана с математическими методами, и «приложениями математики» в науке и технике. Биолог, использующий популяционную модель и применяющий известную математику, занимается не прикладной математикой, а скорее её применением; однако математические биологи поставили проблемы, которые стимулировали рост чистой математики. Математики Пуанкаре и Арнольд, отрицают существование «прикладной математики» и утверждают, что существуют только «приложения математики». Точно так же и нематематики смешивают прикладную математику и приложения математики. Использование и развитие математики для решения производственных задач также называют «промышленной математикой»[1].
Успех современных численных математических методов и программного обеспечения привёл к появлению вычислительной математики, вычислительной науки и вычислительной техники, которые используют высокопроизводительные вычисления для моделирования явлений и решения проблем в науке и технике. Они часто считаются междисциплинарными.

Исторически, математика была наиболее важной в естественных науках и технике. Однако после Второй мировой войны вне физических наук возникли новые области математики, такие как теория игр и теория социального выбора, которые выросли из экономических задач.
С появлением компьютера появились новые приложения: изучение и использование самой новой компьютерной технологии (информатика) для изучения проблем, возникающих в других областях науки (вычислительная наука), а также математика вычислений (например, теоретическая информатика, компьютерная алгебра, численный анализ). Статистика, вероятно, является наиболее распространённой математической наукой, используемой в социальных науках, но и другие области математики, особенно экономическая, становятся всё более полезными в этих дисциплинах.
Академические учреждения по-разному группируют и маркируют курсы, программы и степени по прикладной математике. В некоторых школах есть одно отделение математики, в то время как в других есть отделения прикладной математики и (чистой) математики.
Многие прикладные математические программы (в отличие от кафедр) состоят в основном из перекрестных курсов и совместно назначаемых преподавателей на кафедрах, представляющих приложения. Некоторые программы на степень доктора философии по прикладной математике практически не требуют курсовых работ вне математики, в то время как другие требуют существенной курсовой работы в конкретной области применения. В некотором отношении это различие отражает различие между «применением математики» и «прикладной математикой».
В некоторых университетах Великобритании имеются факультеты прикладной математики и теоретической физики[2][3][4] но в настоящее время гораздо реже встречаются отдельные кафедры чистой и прикладной математики. Заметным исключением из этого является факультет прикладной математики и теоретической физики в Кембриджском университете, на котором существует должность лукасовский профессор математики, которую занимали — Исаак Ньютон, Чарльз Бэббидж, Джеймс Лайтхилл, Поль Дирак и Стивен Хокинг.
Школы с отдельными факультетами прикладной математики варьируются от Университета Брауна, в котором есть крупное отделение прикладной математики, которое предлагает получение степеней через докторантуру, до Университета Санта-Клары, который предлагает только магистр прикладной математики[5]. Исследовательские университеты, разделяющие свои математические факультеты на чистые и прикладные, включают MIT. Университет Бригама Янга также имеет прикладную и вычислительную направленность (ACME), программу, которая позволяет студентам получить высшее образование по математике с акцентом на прикладную математику. Учащиеся этой программы также изучают ещё один навык (информатика, инженерия, физика, чистая математика и т. д.) В дополнение к своим прикладным математическим навыкам.
В ВШЭ есть отделение прикладной математики.
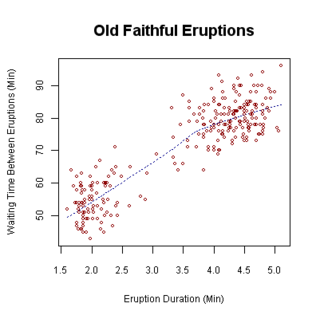
Прикладная математика тесно связана с другими математическими науками.
Научные вычисления включают прикладную математику (особенно численный анализ), вычислительную технику (особенно высокопроизводительные вычисления) и математическое моделирование объектов изучаемых научной дисциплиной.
Информатика опирается на такие дисциплины, как логику, алгебру, комбинаторику и теорию графов.
Исследование операций и науки управления часто преподаются на факультетах инженерии, бизнеса и государственной политики.
Прикладная математика имеет существенное совпадение с дисциплиной статистики. Теоретическая статистика изучает и совершенствует статистические процедуры с помощью математики, а статистические исследования часто поднимают математические вопросы. Статистическая теория опирается на теорию вероятностей и решений и широко использует научные вычисления, анализ и оптимизацию; для планирования экспериментов статистики используют алгебру и комбинаторный дизайн. Прикладные математики и статистики часто работают в отделе математических наук (особенно в колледжах и небольших университетах).
Актуарная наука применяет теорию вероятностей, статистику и экономическую теорию для оценки риска в страховании, финансах и других отраслях и профессиях.
Математическая экономика — это сфера теоретической и прикладной научной деятельности, целью которой является математически формализованное описание экономических объектов, процессов и явлений. Применяемые методы обычно относятся к нетривиальным математическим методам или подходам. Математическая экономика основана на статистике, вероятности, математическом программировании (а также других вычислительных методах), исследовании операций, теории игр и некоторых методах математического анализа. В этом отношении она напоминает (но отличается от финансовой математики), ещё одну часть прикладной математики.
Применимая математика является субдисциплиной прикладной математики, хотя нет единого мнения относительно точного определения[6]. Иногда термин «применимая математика» используется для различия между традиционной прикладной математикой, которая развивалась наряду с физикой, и многими областями математики, которые применимы к современным задачам в мире.
Математики часто проводят различие между «прикладной математикой», с одной стороны, и «применением математики» или «применимой математикой» как внутри, так и вне науки и техники, с другой[6]. Некоторые математики подчеркивают термин применимая математика, чтобы отделить или разграничить традиционные прикладные области от новых приложений, возникающих из областей, которые ранее рассматривались как чистая математика[7]. Например, с этой точки зрения эколог или географ, использующий популяционные модели и применяющий известную математику, занимается не прикладной, а скорее применимой, математикой.
Другие авторы предпочитают описывать применимую математику как объединение «новых» математических приложений с традиционными областями прикладной математики[7][8][9]. Таким образом, термины прикладная математика и применимая математика взаимозаменяемы.
Граница между прикладной математикой и конкретными областями применения размыта. Многие университеты преподают математические и статистические курсы за пределами соответствующих факультетов, в таких областях, как бизнес, инженерия, физика, химия, психология, биология, информатика, научные вычисления и математическая физика.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.