Splay-дерево
Из Википедии, свободной энциклопедии
Расширяющееся (англ. splay tree) или косое дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-чёрных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву.
| Расширяющееся дерево | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | Дерево | |||||||||||||||
| Год изобретения | 1985 | |||||||||||||||
| Автор | Дэниел Слитор и Роберт Андре Тарьян | |||||||||||||||
| Сложность в О-символике | ||||||||||||||||
|
||||||||||||||||
Учётная стоимость в расчёте на одну операцию с деревом составляет .
Расширяющееся дерево придумали Роберт Тарьян и Даниель Слейтор в 1983 году.
Операции
Суммиров вкратце
Перспектива
В другом языковом разделе есть более полная статья Splay tree (англ.). |
Splay (расширение)
Основная операция дерева. Заключается в перемещении вершины в корень при помощи последовательного выполнения трёх операций: Zig, Zig-Zig и Zig-Zag. Обозначим вершину, которую хотим переместить в корень за x, её родителя — p, а родителя p (если существует) — g.
Zig: выполняется, когда p является корнем. Дерево поворачивается по ребру между x и p. Существует лишь для разбора крайнего случая и выполняется только один раз в конце, когда изначальная глубина x была нечётна.

Zig-Zig: выполняется, когда и x, и p являются левыми (или правыми) сыновьями. Дерево поворачивается по ребру между g и p, а потом — по ребру между p и x.
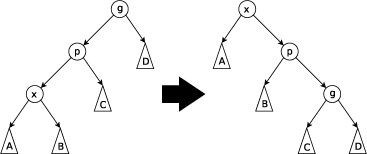
Zig-Zag: выполняется, когда x является правым сыном, а p — левым (или наоборот). Дерево поворачивается по ребру между p и x, а затем — по ребру между x и g.
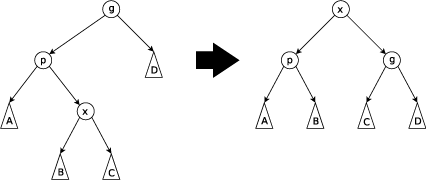
Search (поиск элемента)
Поиск выполняется как в обычном двоичном дереве поиска. При нахождении элемента запускаем Splay для него.
Insert (добавление элемента)
Запускаем Split() от добавляемого элемента (см Split(), напоминание: в нём используется ближайший больший либо равный элемент существующего дерева) и подвешиваем получившиеся деревья за элемент к добавлению.
Delete (удаление элемента)
Находим элемент в дереве, делаем Splay для него, делаем текущим деревом Merge его детей.
Merge (объединение двух деревьев)
Для слияния деревьев T1 и T2, в которых все ключи T1 меньше ключей в T2, делаем Splay для максимального элемента T1, тогда у корня T1 не будет правого ребенка. После этого делаем T2 правым ребенком T1.
Split (разделение дерева на две части)
Для разделения дерева по значению x найдем наименьший элемент, больший или равный x, и сделаем для него Splay. После этого отсоединяем от корня левого ребёнка и возвращаем 2 получившихся дерева.
Реализация
Суммиров вкратце
Перспектива
Одной из реализаций расширяющегося дерева может послужить реализация, использующая 3 указателя в каждой вершине: указатель на правого и левого сыновей, а также на родителя. Это позволяет избежать рекурсивной реализации, что, в свою очередь, повлечет экономию памяти. Минусом в данном случае выступает большее количество присваиваний для обновления указателей, что может сказаться на конечной производительности.
Ниже представлена реализация расширяющегося дерева, использующая по 3 указателя в каждом узле. Также, в данной реализации операция Splay используется во всех основных операциях, выполняемых над деревом — при вставке, удалении и поиске для достижения лучшей сбалансированности дерева.
#ifndef SPLAYTREE_H
#define SPLAYTREE_H
template<typename T> class SplayTree {
private:
struct SplayNode {
Node * leftChild;
Node * rightChild
Node * parent;
T data;
Node (const T & key = T())
: leftChild(nullptr), rightChild(nullptr), parent(nullptr), key(key) {}
~Node () {
delete leftChild;
delete rightChild;
}
} * root;
private:
SplayNode * _Successor(SplayNode * localRoot) const {
SplayNode * successor = localRoot;
if (successor->rightChild != nullptr) {
successor = _Minimum(successor->rightChild);
} else {
while (successor != root
|| successor != successor->parent->leftChild) {
successor = successor->parent;
}
}
return successor;
}
SplayNode * _Predecessor(SplayNode * localRoot) const {
SplayNode * predecessor = localRoot;
if (predecessor->leftChild != nullptr) {
predecessor = _Maximum(predecessor->leftChild);
} else {
while (predecessor != root
|| predecessor != predecessor->parent->rightChild) {
predecessor = predecessor->parent;
}
}
return predecessor;
}
SplayNode * _Minimum(SplayNode * localRoot) const {
SplayNode * minimum = localRoot;
while (minimum->leftChild != nullptr)
minimum = minimum->leftChild;
return minimum;
}
SplayNode * _Maximum(SplayNode * localRoot) const {
SplayNode * maximum = localRoot;
while (maximum->rightChild != nullptr)
maximum = maximum->rightChild;
return maximum;
}
SplayNode * _Search(const T & key) {
SplayNode * searchedElement = root;
while (searchedElement != nullptr) {
if (searchedElement->data < key)
searchedElement = searchedElement->rightChild;
else if (key < searchedElement->data)
searchedElement = searchedElement->leftChild;
else if (searchedElement->data == key) {
_Splay(searchedElement);
return searchedElement;
}
}
return nullptr;
}
void _LeftRotate(SplayNode * localRoot) {
SplayNode * rightChild = localRoot->rightChild;
localRoot->rightChild = rightChild->leftChild;
if (rightChild->leftChild != nullptr)
rightChild->leftChild->parent = localRoot;
_Transplant(localRoot, rightChild);
rightChild->leftChild = localRoot;
rightChild->leftChild->parent = rightChild;
}
void _RightRotate(SplayNode * localRoot) {
SplayNode * leftChild = localRoot->leftChild;
localRoot->leftChild = leftChild->rightChild;
if (leftChild->rightChild != nullptr)
leftChild->rightChild->parent = localRoot;
_Transplant(localRoot, leftChild);
leftChild->rightChild = localRoot;
leftChild->rightChild->parent = leftChild;
}
void _Transplant(SplayNode * localParent, SplayNode * localChild) {
if (localParent->parent == nullptr)
root = localChild;
else if (localParent == localParent->parent->leftChild)
localParent->parent->leftChild = localChild;
else if (localParent == localParent->parent->rightChild)
localParent->parent->rightChild = localChild;
if (localChild != nullptr)
localChild->parent = localParent->parent;
}
void _Splay(SplayNode * pivotElement) {
while (pivotElement != root) {
if (pivotElement->parent == root) {
if (pivotElement == pivotElement->parent->leftChild) {
_RightRotate(pivotElement->parent);
} else if (pivotElement == pivotElement->parent->rightChild) {
_LeftRotate(pivotElement->parent);
}
} else {
// Zig-Zig step.
if (pivotElement == pivotElement->parent->leftChild &&
pivotElement->parent == pivotElement->parent->parent->leftChild) {
_RightRotate(pivotElement->parent->parent);
_RightRotate(pivotElement->parent);
} else if (pivotElement == pivotElement->parent->rightChild &&
pivotElement->parent == pivotElement->parent->parent->rightChild) {
_LeftRotate(pivotElement->parent->parent);
_LeftRotate(pivotElement->parent);
}
// Zig-Zag step.
else if (pivotElement == pivotElement->parent->rightChild &&
pivotElement->parent == pivotElement->parent->parent->leftChild) {
_LeftRotate(pivotElement->parent);
_RightRotate(pivotElement->parent);
} else if (pivotElement == pivotElement->parent->leftChild &&
pivotElement->parent == pivotElement->parent->parent->rightChild) {
_RightRotate(pivotElement->parent);
_LeftRotate(pivotElement->parent);
}
}
}
}
public:
SplayTree() { root = nullptr; }
virtual ~SplayTree() { delete root; }
void Insert(const T & key) {
SplayNode * preInsertPlace = nullptr;
SplayNode * insertPlace = root;
while (insertPlace != nullptr) {
preInsertPlace = insertPlace;
if (insertPlace->data() < key)
insertPlace = insertPlace->rightChild;
else if (key <= insertPlace->data)
insertPlace = insertPlace->leftChild;
}
SplayNode * insertElement = new SplayNode(key);
insertElement->parent = preInsertPlace;
if (preInsertPlace == nullptr)
root = insertElement;
else if (preInsertPlace->data < insertElement->data)
preInsertPlace->rightChild = insertElement;
else if (insertElement->data <= preInsertPlace->data)
preInsertPlace->leftChild = insertElement;
_Splay(insertElement);
}
void Remove(const T & key) {
SplayNode * removeElement = _Search(key);
if (removeElement != nullptr) {
if (removeElement->rightChild == nullptr)
_Transplant(removeElement, removeElement->leftChild);
else if (removeElement->leftChild == nullptr)
_Transplant(removeElement, removeElement->rightChild);
else {
SplayNode * newLocalRoot = _Minimum(removeElement->rightChild);
if (newLocalRoot->parent != removeElement) {
_Transplant(newLocalRoot, newLocalRoot->rightChild);
newLocalRoot->rightChild = removeElement->rightChild;
newLocalRoot->rightChild->parent = newLocalRoot;
}
_Transplant(removeElement, newLocalRoot);
newLocalRoot->leftChild = removeElement->leftChild;
newLocalRoot->leftChild->parent = newLocalRoot;
_Splay(newLocalRoot);
}
delete removeElement;
}
}
bool Search(const T &key) { return _Search(key) != nullptr; }
bool isEmpty() const { return root == nullptr; }
T Successor(const T & key) {
if (_Successor(_Search(key)) != nullptr) {
return _Successor(_Search(key))->getValue();
} else {
return -1;
}
}
T Predecessor(const T & key) {
if (_Predecessor(_Search(key)) != nullptr) {
return _Predecessor(_Search(key))->getValue();
} else {
return -1;
}
}
};
#endif //SPLAYTREE_H
Примечание
Расширяющееся дерево предоставляет самоизменяющуюся структуру — структуру, характеризующуюся тенденцией хранить узлы, к которым часто происходит обращение, вблизи верхушки дерева, в то время как узлы, к которым обращение происходит редко, перемещаются ближе к листьям. Таким образом время обращения к часто посещаемым узлам будет меньше, а время обращения к редко посещаемым узлам — больше среднего.
Расширяющееся дерево не обладает никакими явными функциями балансировки, но процесс скоса узлов к корню способствует поддержанию дерева в сбалансированном виде.
См. также
- Сбалансированные (самобалансирующиеся) деревья:
- Красно-чёрное дерево
- Матричное дерево
- АВЛ-дерево
- Идеально сбалансированное дерево
Литература
- Томас Х. Кормен и др. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296. — ISBN 5-8459-0857-4.
- Daniel Sleator, Robert Tarjan. A data structure for dynamic trees. — Journal of Computer and System Sciences, 1983. — С. 262—391.
Для улучшения этой статьи желательно:
|
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
