Трисекция угла

Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части.

Наряду с задачами о квадратуре круга и удвоении куба является одной из классических неразрешимых задач на построение, известных со времён Древней Греции.

Невозможность построения была доказана Ванцелем в 1837 году. Несмотря на это, в прессе^[1][2][3][4] и даже в некоторых научных журналах^[5] время от времени публикуются ошибочные способы осуществления трисекции угла циркулем и линейкой.

Невозможность построения

П. Л. Ванцель доказал в 1837 году, что трисекция угла ${\displaystyle \alpha }$ разрешима только тогда, когда уравнение

${\displaystyle x^{3}-3x-2\cos \alpha =0.}$

разрешимо в квадратных радикалах.

Например,

• Трисекция осуществима для углов вида ${\displaystyle {2\pi \over n},}$ если целое число ${\displaystyle n}$ не делится на 3.
• Трисекция острого угла прямоугольного треугольника с целыми сторонами, длины которых выражаются взаимно простыми числами, осуществима тогда и только тогда, когда гипотенуза является кубом целого числа^[6].

Построения с помощью дополнительных средств

• Хотя трисекция угла в общем случае невыполнима с помощью циркуля и линейки, существуют кривые, с помощью которых это построение можно выполнить. Улитка Паскаля или трисектриса, квадратриса (в древности тоже называлась трисектрисой), конхоида Никомеда, конические сечения, спираль Архимеда^[7].
• Трисекция возможна при построении с помощью плоского оригами.^[8]

Трисекция угла при помощи невсиса

Рис. 1. Трисекция угла с помощью невсиса

Рис. 2. Трисекция угла (доказательство)

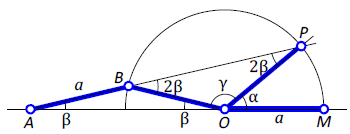
Следующее построение с помощью невсиса предложено Архимедом.

Предположим, что имеется угол ${\displaystyle \alpha =POM}$ (рис. 1). Необходимо построить угол ${\displaystyle \beta }$, величина которого втрое меньше данного: ${\displaystyle \alpha =3\beta }$.

Построим окружность произвольного радиуса ${\displaystyle a}$ с центром в точке ${\displaystyle O}$. Пусть стороны угла пересекаются с окружностью в точках ${\displaystyle P}$ и ${\displaystyle M}$. Продолжим сторону ${\displaystyle OM}$ исходного угла. Возьмём линейку невсиса, отложив на ней диастему ${\displaystyle a}$, и используя прямую ${\displaystyle OM}$ в качестве направляющей, точку ${\displaystyle P}$ в качестве полюса, а полуокружность в качестве целевой линии, строим отрезок ${\displaystyle AB}$. Получим угол ${\displaystyle PAM}$, равный одной трети исходного угла ${\displaystyle \alpha }$.

Доказательство

Рассмотрим треугольник ${\displaystyle ABO}$ (рис. 2). Так как ${\displaystyle AB=BO=a}$, то треугольник равнобедренный, и углы при его основании равны: ${\displaystyle \angle BAO=\angle BOA=\beta }$ . Угол ${\displaystyle \angle PBO}$ как внешний угол треугольника ${\displaystyle ABO}$ равен ${\displaystyle 2\beta }$.

Треугольник ${\displaystyle BPO}$ также равнобедренный, углы при его основании равны ${\displaystyle 2\beta }$, а угол при вершине ${\displaystyle \gamma =180^{\circ }-4\beta }$. С другой стороны, ${\displaystyle \gamma =180^{\circ }-\beta -\alpha }$. Следовательно, ${\displaystyle 180^{\circ }-4\beta =180^{\circ }-\beta -\alpha }$, а значит, ${\displaystyle \alpha =3\beta }$.

См. также

• Улитка Паскаля
• Математика в Древней Греции
• Теорема Морлея — свойство трисектрис углов треугольника.
• Невсис — метод построения, позволяющий выполнить трисекцию угла (не является решением задачи в классической постановке, так как вместо циркуля использует скользящую около полюса линейку).