Собственная энергия

Собственная энергия частицы в квантовой теории поля — это полная энергия частицы с учётом изменений в окружающем пространстве (вакууме). Обозначают ${\displaystyle \Sigma }$, и представляет собой вклад в энергию частицы или эффективную массу из-за взаимодействия между частицей и её окружением. В электростатике энергия, необходимая для формирования распределения зарядов, принимает форму собственной энергии за счёт перемещения составляющих зарядов из бесконечности, где электрическая сила стремится к нулю. В контексте физики конденсированного состояния, для электронов — квазичастицам, движущимся в материале, собственная энергия или часто говорят о собственной энергетической части (полной энергии поскольку ряд теории возмущений обычно учитывает только часть диаграмм для конкретного приближения) представляет собой потенциал, который ощущает электрон из-за взаимодействия с окружающей средой. Поскольку электроны отталкивают друг друга, движущийся электрон поляризует или заставляет смещаться электроны поблизости, а затем изменяет потенциал движущихся электронных полей.

Свойства

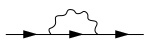
Математически эта энергия равна так называемому значению на массовой оболочке оператора собственной энергии в импульсном представлении (точнее, этому значению умноженному на ${\displaystyle \hbar }$). В этом или других представлениях (таких как представление пространства-времени) собственная энергия наглядно (и кратко) представлена с помощью диаграмм Фейнмана, таких как показанная ниже. На этой конкретной диаграмме три прямые линии со стрелками представляют частицы или пропагаторы частиц, а волнистая линия — взаимодействие между частицами; удалив (или ампутировав) крайнюю левую и крайнюю правую прямые линии на диаграмме, показанной ниже (эти так называемые внешние линии соответствуют заданным значениям, например, для импульса и энергии, или четырёхимпульса), сохраняется вклад в оператор собственной энергии (например, в импульсном представлении). Используя небольшое количество простых правил, каждая диаграмма Фейнмана выражается в соответствующей алгебраической форме.

В общем, значение оператора собственной энергии на массовой оболочке в импульсном представлении комплекснозначное. В таких случаях именно реальная часть этой собственной энергии отождествляется с физической собственной энергией (называемой выше «собственной энергией» частицы); обратная мнимая часть является мерой времени жизни исследуемой частицы. Для ясности элементарные возбуждения, или одетые частицы (см. квазичастицы), во взаимодействующих системах отличаются от стабильных частиц в вакууме; их функции состояния состоят из сложных суперпозиций собственных состояний лежащей в основе многочастичной системы, которые лишь на мгновение, если вообще ведут себя как те, которые специфичны для свободных частиц; вышеупомянутое время жизни — это время, в течение которого одетая частица ведёт себя так, как если бы она была одиночной частицей с чётко определёнными импульсом и энергией.

Оператор собственной энергии (часто обозначаемый ${\displaystyle \Sigma _{}^{}}$) относится к голым и одетым пропагаторам (часто обозначается ${\displaystyle G_{0}^{}}$ и ${\displaystyle G_{}^{}}$ соответственно) через уравнение Дайсона:

${\displaystyle G=G_{0}^{}+G_{0}\Sigma G.}$

Умножение слева на обратный оператор ${\displaystyle G_{0}^{-1}}$ к оператору ${\displaystyle G_{0}}$ и справа от ${\displaystyle G^{-1}}$ даёт

${\displaystyle \Sigma =G_{0}^{-1}-G^{-1}.}$

Фотон и глюон не приобретают массу в результате перенормировки, поскольку калибровочная симметрия защищает их от приобретение массы. Это следствие тождества Уорда. W-бозон и Z-бозон получают массы посредством механизма Хиггса; они действительно подвергаются перенормировке массы посредством перенормировки теории электрослабого взаимодействия.

Нейтральные частицы с внутренними квантовыми числами могут смешиваться друг с другом посредством образования виртуальных пар. Основным примером этого явления является смешивание нейтральных каонов. При соответствующих упрощающих предположениях этот процесс описывается без использования квантовой теории поля.

Литература

• A. L. Fetter, and J. D. Walecka, Quantum Theory of Many-Particle Systems (McGraw-Hill, New York, 1971); (Dover, New York, 2003)
• J. W. Negele, and H. Orland, Quantum Many-Particle Systems (Westview Press, Boulder, 1998)
• A. A. Abrikosov, L. P. Gorkov and I. E. Dzyaloshinski (1963): Methods of Quantum Field Theory in Statistical Physics Englewood Cliffs: Prentice-Hall.
• Alexei M. Tsvelik. Quantum Field Theory in Condensed Matter Physics. — 2nd. — Cambridge University Press, 2007. — ISBN 978-0-521-52980-8.
• A. N. Vasil’ev The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics (Routledge Chapman & Hall 2004); ISBN 0-415-31002-4; ISBN 978-0-415-31002-4
• John E. Inglesfield. The Embedding Method for Electronic Structure. — IOP Publishing, 2015. — ISBN 978-0-7503-1042-0.