Loading AI tools
Сложная система — система, состоящая из множества взаимодействующих составляющих (подсистем), вследствие чего она приобретает новые свойства, которые отсутствуют на подсистемном уровне и не могут быть сведены к свойствам подсистемного уровня. Примерами сложных систем являются глобальный климат Земли, организмы, человеческий мозг, инфраструктура, такая как электросеть, транспортные или коммуникационные системы, сложное программное обеспечение и электронные системы, социальные и экономические организации (например, города), экосистема, живая клетка и, в конечном счете, вся вселенная.
Сложные системы — это системы, поведение которых трудно смоделировать из-за зависимостей, конкуренции, отношений или других типов взаимодействия между их частями или между данной системой и ее окружением. «Сложные» системы имеют определенные свойства, возникающие из этих отношений, такие как нелинейность динамики, эмерджентность, спонтанный порядок, адаптация и петли обратной связи, среди прочего. Поскольку такие системы появляются в самых разных областях, общие черты между ними стали предметом их самостоятельной области исследований. Во многих случаях полезно представить такую систему как сеть, где узлы представляют компоненты и связи между ними.
Термин «сложные системы» часто относится к изучению сложных систем, что представляет собой подход к науке, который исследует, как отношения между частями системы порождают ее коллективное поведение и как система взаимодействует и формирует отношения с окружающей средой[1]. Как междисциплинарная область, сложные системы получают вклад из многих различных областей, таких как изучение самоорганизации и критических явлений из физики, изучение спонтанного порядка из социальных наук, хаоса из математики, адаптации из биологии и многих других. Поэтому сложные системы часто используются как широкий термин, охватывающий исследовательский подход к проблемам во многих различных дисциплинах, включая статистическую физику, теорию информации, нелинейную динамику, антропологию, информатику, метеорологию, социологию, экономику, психологию и биологию.
Системы
Сложные системы в основном связаны с поведением и свойствами систем. Система — комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей (ГОСТ Р ИСО МЭК 15288-2005)[2]. Элементы, лежащие вне системы, затем становятся частью системной среды.
Система может проявлять свойства, которые приводят к поведению, отличному от свойств и поведения ее частей; эти общесистемные или глобальные свойства и поведение являются характеристиками того, как система взаимодействует с окружающей средой или предстает перед ней, или того, как ведут себя ее части (скажем, в ответ на внешние стимулы) в силу того, что они находятся внутри системы. Понятие поведения подразумевает, что изучение систем также связано с процессами, происходящими во времени (или, в математике, с некоторой другой параметризацией фазового пространства). Из-за их широкой междисциплинарной применимости системные концепции играют центральную роль в сложных системах.
Что касается сложных систем, теория систем делает акцент на том, как отношения и зависимости между частями системы могут определять общесистемные свойства. Это также способствует междисциплинарной перспективе изучения сложных систем: представлению о том, что общие свойства связывают системы между дисциплинами, оправдывая поиск подходов к моделированию, применимых к сложным системам, где бы они ни появлялись. Конкретные концепции, важные для сложных систем, такие как эмерджентность, циклы обратной связи и адаптация, также берут свое начало в теории систем.
Сложность
Сложность системы означает то, что поведение систем не может быть легко выведено из ее свойств. До сих пор не появилось полностью общей теории сложных систем для решения этих проблем, поэтому исследователи должны решать их в контексте конкретной предметной области. Исследователи сложных систем решают эти проблемы, рассматривая главную задачу моделирования как захват, а не уменьшение сложности соответствующих интересующих их систем [3].
Хотя общепринятого точного определения сложности пока не существует, существует множество архетипических примеров сложности. Системы могут быть сложными, если, например, они обладают хаотическим поведением (поведение, проявляющее чрезвычайную чувствительность к начальным условиям, среди других свойств), или если они обладают эмерджентными свойствами (свойствами, которые не проявляются из их компонентов по отдельности, но которые являются результатом отношений и зависимостей, которые они образуют, когда помещены вместе в системе), или если они с вычислительной точки зрения трудно поддаются моделированию (если они зависят от ряда параметров, которые слишком быстро растут по отношению к размеру системы).
Классификация сложностей
Согласно Питеру Сенге, системная сложность существует в двух основных формах:
- Сложность детализации (структурная сложность) возникает в результате большого количества систем, системных элементов и установленных связей в любой из двух основных топологий (иерархия или сеть). Эта сложность связана с системами, как они есть; а именно, с их статическим существованием.
- Динамическая сложность (поведенческая сложность) связана с взаимосвязями, которые возникают между готовыми, функционирующими системами в процессе их работы, т. е. между ожидаемым и даже неожидаемым поведением, которое фактически возникает.
Уоррен Уивер [Weaver, 1948][4] сформулировал исходную точку зрения, выделив следующие категории сложности: организованная простота, организованная сложность, беспорядочная сложность. Эти категории и более поздние размышления, в частности Флада и Карсона [Flood and Carson, 1993] авторы книги, дают основания для использования приведенной ниже классификации сложности:
- Организованная простота имеет место, когда есть небольшое количество существенных факторов и большое количество менее существенных и/или несущественных факторов. Изначально ситуация может показаться сложной, но после ее изучения менее существенные и несущественные факторы могут быть исключены из картины и может быть обнаружена скрытая простота.
- Организованная сложность преобладает в таких физических и абстрактных системах, структура которых организована так, чтобы быть понятной, и поэтому податливой ученым при описании сложного поведения и структурировании процесса создания сложных систем и управления их жизненными циклами. Это богатство, которое не должно быть чрезмерно упрощено.
- Беспорядочная сложность возникает, когда имеется много переменных, которые демонстрируют в высокой степени случайное, беспорядочное поведение. Она также может являться результатом отсутствия необходимого контроля над структурой сложных неоднородных систем по причине неадекватного управления архитектурой в течение жизненного цикла системы (ползучей сложности).
- Сложность, связанная с людьми, возникает там, где восприятие любой системы вызывает чувство сложности. В этом контексте люди становятся «системами наблюдений». Мы могли бы также связать эту категорию с системами, в которых люди являются элементами и могут основательно поспособствовать организованной простоте, организованной сложности и беспорядочной сложности. Разумное или неразумное поведение отдельных лиц в конкретных ситуациях, естественно, является существенным фактором по отношению к сложности.
Сети
Взаимодействующие компоненты сложной системы образуют сеть [5], которая представляет собой совокупность дискретных объектов и связей между ними, обычно изображаемых в виде графа вершин, соединенных ребрами. Сети могут описывать отношения между отдельными лицами внутри организации, между логическими элементами в схеме, между генами в сетях регулирования генов или между любым другим набором связанных объектов.
Сети часто описывают источники сложности в сложных системах[6]. Таким образом, изучение сложных систем как сетей открывает множество полезных применений теории графов и сетевой науки. Многие сложные системы, например, также являются сложными сетями, которые обладают такими свойствами, как фазовые переходы и распределения степеней, которые легко поддаются эмерджентному или хаотическому поведению. Тот факт, что число ребер в полном графе растет квадратично по отношению к числу вершин, проливает дополнительный свет на источник сложности в больших сетях: по мере роста сети количество связей между объектами быстро затмевает количество объектов в сети. [7]
Нелинейность

Сложные системы часто имеют нелинейное поведение, то есть они могут по-разному реагировать на одни и те же входные данные в зависимости от своего состояния или контекста. В математике и физике нелинейность описывает системы, в которых изменение размера входных данных не приводит к пропорциональному изменению размера выходных данных. При заданном изменении на входе такие системы могут давать значительно большие или меньшие пропорциональные изменения на выходе или даже вообще не давать выход, в зависимости от текущего состояния системы или значений ее параметров.
Особый интерес для сложных систем представляют нелинейные динамические системы, которые представляют собой системы дифференциальных уравнений, которые имеют один или несколько нелинейных членов. Некоторые нелинейные динамические системы, такие как система Лоренца, могут вызывать математическое явление, известное как хаос. Хаос в применении к сложным системам относится к чувствительной зависимости от начальных условий или «эффекту бабочки», который может проявляться в сложной системе. В такой системе небольшие изменения начальных условий могут привести к совершенно иным результатам. Таким образом, хаотичное поведение может быть чрезвычайно сложно смоделировать численно, поскольку небольшие ошибки округления на промежуточном этапе вычислений могут привести к тому, что модель будет генерировать совершенно неточные выходные данные. Кроме того, если сложная система возвращается в состояние, похожее на то, в котором она находилась ранее, она может вести себя совершенно по-другому в ответ на одни и те же стимулы, поэтому хаос также создает проблемы для экстраполяции опыта.
Эмерджентность

Другой общей чертой сложных систем является наличие эмерджентного поведения и свойств: это черты системы, которые не проявляются отдельно от ее компонентов, а являются результатом взаимодействий, зависимостей или отношений, которые они формируют, когда они помещаются вместе в систему. Эмерджентность широко описывает внешний вид такого поведения и свойств и имеет приложения к системам, изучаемым как в социальных, так и в физических науках. Хотя эмерджентность часто используется для обозначения только проявления незапланированного организованного поведения в сложной системе, эмерджентность также может относиться к распаду организации; он описывает любые явления, которые трудно или даже невозможно предсказать по более мелким объектам, из которых состоит система.
Одним из примеров сложной системы, эмерджентные свойства которой широко изучались, являются клеточные автоматы. В клеточном автомате сетка ячеек, каждая из которых имеет одно из конечного множества состояний, развивается в соответствии с простым набором правил. Эти правила управляют «взаимодействием» каждой ячейки со своими соседями. Хотя правила определены только локально, было показано, что они способны создавать глобально интересное поведение, например, в «Игре жизни» Конвея.
Характеристики
Сложные системы могут иметь следующие особенности:[9]
- Сложные системы могут быть открытыми
- Сложные системы обычно являются открытыми системами, то есть они существуют в термодинамическом градиенте и рассеивают энергию. Другими словами, сложные системы часто далеки от энергетического равновесия: но, несмотря на этот поток, может существовать стабильность модели,[10] см. синергетику.
- Сложные системы могут демонстрировать критические переходы
- Критические переходы — это резкие сдвиги в состоянии экосистем, климата,финансовых систем или других сложных систем, которые могут произойти, когда изменяющиеся условия проходят критическую точку или точку бифуркации[11][12][13][14]. «Направление критического замедления» в пространстве состояний системы может указывать на будущее состояние системы после таких переходов, когда запаздывающие отрицательные обратные связи, приводящие к колебательной или другой сложной динамике, слабы.[15]
- Сложные системы могут быть вложенными
- Компоненты сложной системы сами по себе могут быть сложными системами. Например,экономика состоит из организаций, состоящих из людей, состоящих из ячеек, которые представляют собой сложные системы. Организация взаимодействий в сложных двусторонних сетях также может быть вложенной. В частности, было обнаружено, что двусторонние экологические и организационные сети взаимовыгодного взаимодействия имеют вложенную структуру.[16][17] Эта структура способствует косвенному содействию и способности системы сохраняться во все более суровых условиях, а также потенциалу для крупномасштабных системных смен режима.[18][19]
- Динамическая сеть множественности
- Помимо правил связывания, важна динамическая сеть сложной системы. Часто используются небольшие мировые или безмасштабные сети [20][21], которые имеют много локальных взаимодействий и меньшее количество межобластных соединений. Природные сложные системы часто демонстрируют такие топологии. Например, в коре головного мозга человека мы видим плотную локальную связь и несколько очень длинных проекций аксонов между областями внутри коры и другими областями мозга.
- Может производить эмерджентные явления
- Сложные системы могут проявлять эмерджентное поведение, то есть, хотя результаты могут в достаточной степени определяться активностью основных компонентов системы, они могут обладать свойствами, которые можно изучать только на более высоком уровне. Например, эмпирические пищевые сети демонстрируют регулярные, инвариантные к масштабу характеристики в водных и наземных экосистемах при изучении на уровне сгруппированных «трофических» видов.[22][23] Другой пример дают термиты в кургане, физиология, биохимия и биологическое развитие которых находятся на одном уровне анализа, тогда как их социальное поведение и строительство кургана — это свойство, возникающее из коллекции термитов и требующее анализа на другом уровне.
- Отношения не линейны
- С практической точки зрения это означает, что небольшое возмущение может вызвать большой эффект (см. эффект бабочки), пропорциональный эффект или даже полное отсутствие эффекта. В линейных системах следствие всегда прямо пропорционально причине. См. нелинейность.
- Отношения содержат петли обратной связи
- В сложных системах всегда присутствуют как отрицательная (демпфирующая), так и положительная (усиливающая) обратная связь. Эффекты поведения элемента возвращаются таким образом, что изменяется сам элемент.
Хотя, возможно, люди изучали сложные системы на протяжении тысячелетий, современное научное изучение сложных систем относительно молодо по сравнению с устоявшимися областями науки, такими как физика и химия. История научного изучения этих систем следует нескольким различным направлениям исследований.
В области математики, возможно, самым большим вкладом в изучение сложных систем стало открытие хаоса в детерминированных системах, особенности некоторых динамических систем, которая тесно связана с нейролинейностью.[24] Изучение нейронных сетей также было неотъемлемой частью развития математики, необходимой для изучения сложных систем.
Понятие самоорганизующихся систем связано с работами в области неравновесной термодинамики, в том числе с работами, впервые проведенными химиком и нобелевским лауреатом Ильей Пригожиным в его исследовании диссипативных структур. Еще более древней является работа Хартри-Фока по уравнениям квантовой химии и более поздним расчетам структуры молекул, которую можно рассматривать как один из самых ранних примеров возникновения и эмерджентных целостностей в науке. Одной из сложных систем, содержащих людей, является классическая политическая экономия шотландского просвещения,позже развитая австрийской школой экономики, которая утверждает, что порядок в рыночных системах является спонтанным (или возникающим) в том смысле, что он является результатом человеческих действий, но не исполнением какого-либо человеческого замысла.[25][26]
Сложность и моделирование
Одним из главных вкладов Фридриха Хайека в раннюю теорию сложности является его различие между способностью человека предсказывать поведение простых систем и его способностью предсказывать поведение сложных систем с помощью научного моделирования. Он считал, что экономика и науки о сложных явлениях в целом, которые, по его мнению, включали биологию, психологию и так далее, не могут быть смоделированы по образцу наук, которые имеют дело с простыми явлениями, такими как физика.[27] Хайек, в частности, объяснил бы, что сложные явления с помощью моделирования могут допускать только шаблонные предсказания по сравнению с точными предсказаниями, которые могут быть сделаны из несложных явлений.[28]
Теория сложности и хаоса
Теория сложности уходит корнями в теорию хаоса, которая, в свою очередь, берет свое начало более века назад в работах французского математика Анри Пуанкаре. Хаос иногда рассматривается как чрезвычайно сложная информация, а не как отсутствие порядка.[29] Хаотические системы остаются детерминированными, хотя их долгосрочное поведение может быть трудно предсказать с какой-либо точностью. Обладая совершенным знанием начальных условий и соответствующих уравнений, описывающих поведение хаотической системы, теоретически можно делать совершенно точные предсказания системы, хотя на практике это невозможно сделать с произвольной точностью. Илья Пригожин утверждал[30], что сложность недетерминирована и не дает никакого способа точно предсказать будущее.[31]
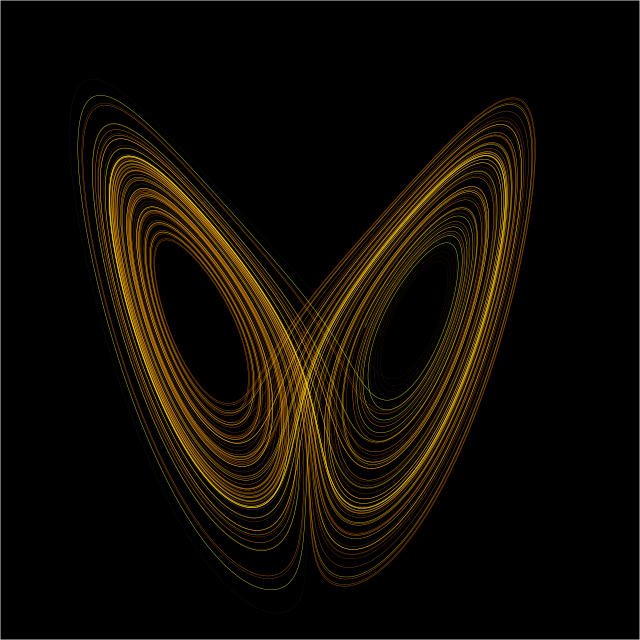
Появление теории сложности показывает область между детерминированным порядком и случайностью, которая является сложной.Это называется "гранью хаоса".[32] Например, при анализе сложных систем чувствительность к начальным условиям не является столь важным вопросом, как в рамках теории хаоса, в которой она преобладает. Как заявил Коландер,[33] изучение сложности противоположно изучению хаоса. Сложность заключается в том, что огромное количество чрезвычайно сложных и динамичных наборов отношений может генерировать некоторые простые модели поведения, тогда как хаотическое поведение в смысле детерминированного хаоса является результатом относительно небольшого количества нелинейных взаимодействий.[34] Недавние примеры из экономики и бизнеса см. Stoop et al.[35]. который обсудил положение Android на рынке, Орландо[36], который объяснил корпоративную динамику с точки зрения взаимной синхронизации и упорядочения хаоса всплесков в группе хаотически взрывающихся ячеек, и Орландо и др.[37]. который смоделировал финансовые данные (индекс финансового стресса, свопы и акции, развивающиеся и развитые, корпоративные и государственные, краткосрочные и долгосрочные) с помощью низкоразмерной детерминированной модели.
Следовательно, основное различие между хаотическими системами и сложными системами заключается в их истории.[38] Хаотические системы не полагаются на свою историю, как сложные. Хаотическое поведение подталкивает систему, находящуюся в равновесии, к хаотичному порядку, что означает, другими словами, выход за пределы того, что мы традиционно определяем как «порядок». Они развиваются в критическом состоянии, созданном историей необратимых и неожиданных событий, которые физик Мюррей Гелл-Манн назвал «накоплением замороженных случайностей».[39] В некотором смысле хаотические системы можно рассматривать как подмножество сложных систем, отличающееся именно этим отсутствием исторической зависимости. Многие действительно сложные системы на практике и в течение длительного, но ограниченного периода времени являются устойчивыми. Однако они обладают потенциалом радикального качественного изменения вида при сохранении системной целостности. Метаморфоза служит, возможно, больше, чем метафора для таких преобразований.
Управление сложностью
Поскольку проекты и поглощения становятся все более сложными, перед компаниями и правительствами стоит задача найти эффективные способы управления мегазакупками, такими как боевые системы будущего армии. Приобретения, такие как БСБ, опираются на сеть взаимосвязанных частей, которые взаимодействуют непредсказуемым образом. По мере того как приобретения становятся все более сетецентричными и сложными, предприятия будут вынуждены находить способы управления сложностью, в то время как правительствам будет предложено обеспечить эффективное управление для обеспечения гибкости и отказоустойчивости.[40]
Экономика сложности
За последние десятилетия в развивающейся области экономики сложности были разработаны новые инструменты прогнозирования для объяснения экономического роста. Так обстоит дело с моделями, построенными Институтом Санта-Фе в 1989 году, и более поздним индексом экономической сложности (ECI), введенным физиком из Массачусетского технологического института Сезаром А. Идальго и экономистом из Гарварда Рикардо Хаусманом. Основываясь на ECI, Хаусманн, Идальго и их команда из Обсерватории экономической сложности подготовили прогнозы ВВП на 2020 год. Количественный анализ повторяемости был использован для определения характеристик бизнес-циклов и экономического развития. С этой целью Орландо и др. [41] разработали так называемый индекс корреляции количественной оценки повторяемости (RQCI) для проверки корреляций RQA с выборочным сигналом, а затем исследовали применение к бизнес-временным рядам. Было доказано, что указанный индекс обнаруживает скрытые изменения во временных рядах. Далее, Орландо и др.[42] на обширном наборе данных показали, что анализ количественной оценки повторяемости может помочь в прогнозировании переходов от ламинарных (т.е. регулярных) к турбулентным (т.е. хаотическим) фазам, таким как ВВП США в 1949, 1953 и т.д. И последнее, но не менее важное: было продемонстрировано, что количественный анализ повторяемости может выявлять различия между макроэкономическими переменными и выявлять скрытые особенности экономической динамики.
Сложность и обучение
Сосредоточив внимание на вопросах настойчивости студентов в учебе, Форсман, Молл и Линдер исследуют "жизнеспособность использования науки о сложности в качестве основы для расширения методологических приложений для исследований в области физического образования", обнаружив, что "анализ социальных сетей с точки зрения науки о сложности предлагает новую и мощную применимость в широком диапазоне ПО темам".[43]
Сложность в биологии и нейронауках
В рамках развивающейся области фрактальной физиологии телесные сигналы, такие как частота сердечных сокращений или мозговая активность, характеризуются с использованием энтропии или фрактальных индексов. Цель часто состоит в том, чтобы оценить состояние и работоспособность основной системы и диагностировать потенциальные расстройства и болезни.
Сложность и наука о сетях
Сложная система обычно состоит из множества компонентов и их взаимодействий. Такая система может быть представлена сетью, где узлы представляют компоненты, а связи представляют их взаимодействия. Например, Интернет можно представить как сеть, состоящую из узлов (компьютеров) и связей (прямых соединений между компьютерами). Другие примеры сложных сетей включают социальные сети, взаимозависимости финансовых учреждений, сети авиакомпаний и биологические сети.
Шкала Боулдинга
Американский экономист Кеннет Боулдинг предложил шкалу сложности систем, состоящую из девяти уровней[44][45].
- Уровень статической структуры. К таким системам можно отнести: расположение электронов в атоме, строение кристалла, анатомию животного и т. п.
- Простые детерминированные динамические системы. Примеры: Солнечная система, механическое устройство, структура теории наук вроде физики и химии.
- Уровень управляющего механизма или кибернетической системы, уровень термостата. Система характерна тем, что стремится к сохранению равновесия.
- Уровень открытой или самосохраняющейся системы, уровень клетки. Кроме биологических объектов, к этому уровню можно отнести реки и пожары.
- Уровень генетического сообщества. Примерами могут являться растения. Характерен специализацией клеток. Система характеризуется разрозненностью приёмников информации и неспособностью обрабатывать её большие объёмы.
- Уровень животных. Системы характеризуются мобильностью, целесообразным поведением, самосохранением. Развитые информационные рецепторы, нервная система, мозг.
- Уровень человека. Самосознание, отличное от простого самосохранения. Рефлексия. Речь.
- Уровень социальной организации.
- Уровень трансцендентальных систем, не поддающихся анализу, но обладающих структурой.
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.