Показательная функция
математическая функция a^x Из Википедии, свободной энциклопедии
Показательная функция — математическая функция , где называется основанием степени, а — показателем степени.
- В вещественном случае основание степени — некоторое неотрицательное вещественное число (для отрицательных чисел возведение в вещественную нецелочисленную степень не определено), а аргументом функции является вещественный показатель степени.
- В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
- В самом общем виде — , введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной). При этом из-за того, что любое положительное основание может быть представлено в виде степени числа е (), понятие «экспонента» часто употребляют как синоним «показательной функции».
Вещественная функция
Суммиров вкратце
Перспектива
Определение показательной функции
Пусть — неотрицательное вещественное число, — рациональное число: . Тогда определяется, исходя из свойств степени с рациональным показателем, по следующим правилам.
- Если , то .
- Если и , то .
- Значение не определено (см. Ноль в степени ноль).
- Если и , то .
- Значение при не определено.
Для произвольного вещественного показателя значение можно определить как предел последовательности
где — последовательность рациональных чисел, сходящихся к . То есть
Свойства
Свойства возведения в степень:
- / =
Промежутки монотонности:
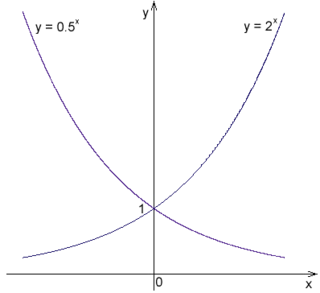
При показательная функция всюду возрастает, причём:
- (для всякого )
При функция, соответственно, убывает, причём:
- (для всякого )
То есть показательная функция растёт на бесконечности быстрее любой полиномиальной. Большая скорость роста может быть проиллюстрирована, например, задачей о складывании бумаги.
Обратная функция:
По аналогии с введением функции корня для степенной введём логарифмическую функцию, обратную показательной:
- (логарифм по основанию )
Число е:
Отметим уникальное свойство показательной функции, найдём (такое число , производная показательной функции которого равна самой функции):
Возможность определения легко увидеть после сокращения на :
Выбирая , окончательно получим число Эйлера:
Отметим, что функцию можно иначе представить в виде ряда: (справедливость легко установить почленным дифференцированием):
Откуда имеем более точное приближение:
Единственность числа легко показать, варьируя . Действительно, если пройдёт где-то выше, чем , то на том же промежутке найдётся область, где .
Дифференцирование:
Используя функцию натурального логарифма , можно выразить показательную функцию с произвольным положительным основанием через экспоненту. По свойству степени: , откуда по свойству экспоненты и по правилу дифференцирования сложной функции:
Неопределённый интеграл:
Потенцирование и антилогарифм

Потенцирование (от нем. potenzieren[К 1]) — нахождение числа по известному значению его логарифма[1], то есть решение уравнения . Из определения логарифма вытекает, что , таким образом, возведение в степень может быть названо другими словами «потенцированием по основанию », или вычислением показательной функции от .
Антилогарифм[2] числа x — результат потенцирования, то есть число, логарифм которого (при заданном основании ) равен числу [2][3]:
Термин «антилогарифм» введен Валлисом в 1693 году[4]. Как самостоятельное понятие антилогарифм используется в логарифмических таблицах[5], логарифмических линейках, микрокалькуляторах. Например, для извлечения кубического корня из числа по логарифмическим таблицам следует найти логарифм числа разделить его на 3 и затем (по таблице антилогарифмов) найти антилогарифм результата.
Аналогично логарифмам, антилогарифм по основанию или 10 называется натуральным[6] или десятичным, соответственно.
Антилогарифм также называют обращённым логарифмом[3].
В инженерных калькуляторах потенцирование стандартно представлено в виде двух функций: и .
Комплексная функция
Суммиров вкратце
Перспектива
Для расширения экспоненты на комплексную плоскость определим её с помощью того же ряда, заменив вещественный аргумент на комплексный:
Эта функция имеет те же основные алгебраические и аналитические свойства, что и вещественная. Отделив в ряде для вещественную часть от мнимой, мы получаем знаменитую формулу Эйлера:
Отсюда вытекает, что комплексная экспонента периодична вдоль мнимой оси:
Показательная функция с произвольным комплексным основанием и показателем степени легко вычисляется с помощью комплексной экспоненты и комплексного логарифма.
Пример: ; поскольку (главное значение логарифма), окончательно получаем: .
См. также
Примечания
Литература
Wikiwand - on
Seamless Wikipedia browsing. On steroids.









![{\displaystyle a^{x}={\sqrt[{n}]{a^{m}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5f7ed005a337fcce2a069abf6e36733907f1915b)






![{\displaystyle a^{x}={\frac {1}{a^{|x|}}}={\frac {1}{\sqrt[{n}]{a^{|m|}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b05f2a459b247016c81f42ac03131655061bd78d)















































