Формула Эйлера

У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Формулы.

Формула Эйлера связывает комплексную экспоненту с тригонометрическими функциями. Названа в честь Леонарда Эйлера, который её ввёл.

Геометрический смысл формулы Эйлера

Формула Эйлера утверждает, что для любого вещественного числа ${\displaystyle x}$ выполнено следующее равенство:

${\displaystyle e^{ix}=\cos x+i\sin x}$,

где ${\displaystyle e}$ — одна из важнейших математических констант, определяющаяся следующей формулой: ${\displaystyle e=\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}}$,

${\displaystyle i}$ — мнимая единица.

История

Формула Эйлера впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году^[1] и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum), которая была издана в 1722 году, уже после смерти автора^[2]. Котс привёл её как небольшое предложение среди множества геометрических построений, которое после перевода на современный математический язык и исправления ошибки в знаке, имеет вид^[3]:

${\displaystyle \ln(\cos x+i\sin x)=ix}$.

Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748)^[4], построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя у К. Весселя.

Производные формулы

При помощи формулы Эйлера можно определить функции ${\displaystyle \sin }$ и ${\displaystyle \cos }$ следующим образом:

${\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}$,

${\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}$.

Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть ${\displaystyle x=iy}$, тогда:

${\displaystyle \sin iy={\frac {e^{-y}-e^{y}}{2i}}=i\mathop {\mathrm {sh} } \,y}$,

${\displaystyle \cos iy={\frac {e^{-y}+e^{y}}{2}}=\mathop {\mathrm {ch} } \,y}$.

Известное тождество Эйлера, связывающее пять фундаментальных математических констант:

${\displaystyle e^{i\pi }+1=0}$

является частным случаем формулы Эйлера при ${\displaystyle x=\pi }$.

Применение в теории чисел

Основная статья: Тригонометрическая сумма

В аналитической теории чисел часто рассматриваются специальные суммы вида ${\displaystyle \sum \limits _{x\in X}{e^{2\pi if(x)}}}$, где ${\displaystyle X}$ — некоторое множество рассматриваемых объектов, а ${\displaystyle f:\ X\to {\mathbb {R} }}$ — функция, отражающая изучаемые свойства объектов.

Для теории чисел, изучающей целые числа, имеют значение прежде всего выводимые из формулы Эйлера индикаторные тождества, касающиеся произвольного целого числа ${\displaystyle n}$.

${\displaystyle \sum \limits _{k=1}^{p}{e^{2\pi {\frac {nk}{p}}i}}=p[p|n]=\left\{{\begin{matrix}p,&n\equiv 0{\pmod {p}}\\0,&n\not \equiv 0{\pmod {p}}\end{matrix}}\right.}$

${\displaystyle \int \limits _{0}^{1}{e^{2\pi n\alpha i}}=[n=0]=\left\{{\begin{matrix}1,&n=0\\0,&n\not =0\end{matrix}}\right.}$

Применение в комплексном анализе

Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: ${\displaystyle x=a+ib=|x|(\cos \varphi +i\sin \varphi )=|x|e^{i\varphi }}$.

Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: ${\displaystyle x=|x|e^{i\varphi }}$, ${\displaystyle x^{n}=|x|^{n}e^{ni\varphi }}$. Геометрический смысл данной формулы следующий: при возведении числа ${\displaystyle x}$ в степень ${\displaystyle n}$ его расстояние до центра возводится в степень ${\displaystyle n}$, а угол поворота относительно оси ${\displaystyle OX}$ увеличивается в ${\displaystyle n}$ раз.

Формула возведения в степень верна не только для целых ${\displaystyle n}$, но и для вещественных. В частности, показательная запись числа позволяет находить корни любой степени из любого комплексного числа.

Взаимосвязь с тригонометрией

Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:

${\displaystyle \cos x=\mathrm {Re} \left(e^{ix}\right)={e^{ix}+e^{-ix} \over 2}}$

${\textstyle \sin x=\mathrm {Im} \left(e^{ix}\right)={e^{ix}-e^{-ix} \over 2i}.}$

Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:

${\displaystyle e^{ix}=\cos x+i\sin x\;}$

${\textstyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;}$

с последующим решением относительно синуса или косинуса.

Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

${\displaystyle \cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)}$

${\displaystyle \sin(iy)={e^{-y}-e^{y} \over 2i}=-{1 \over i}{e^{y}-e^{-y} \over 2}=i\sinh(y).}$

Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Например:

${\displaystyle {\begin{aligned}\cos x\cdot \cos y&={\frac {(e^{ix}+e^{-ix})}{2}}\cdot {\frac {(e^{iy}+e^{-iy})}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}\left[\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}\right].\end{aligned}}}$

Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:

${\displaystyle {\begin{aligned}\cos(nx)&=\mathrm {Re} \{\ e^{inx}\ \}=\mathrm {Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot (e^{ix}+e^{-ix}-e^{-ix})\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot \underbrace {(e^{ix}+e^{-ix})} _{2\cos(x)}-e^{i(n-2)x}\ \}\\&=\cos[(n-1)x]\cdot 2\cos(x)-\cos[(n-2)x].\end{aligned}}}$

Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).

Доказательство

Доказательство формулы Эйлера можно провести с использованием ряда Маклорена. Разложим функцию ${\displaystyle e^{ix}}$ в ряд Тейлора в окрестности точки a = 0 (в ряд Маклорена) по степеням ${\displaystyle x}$. Получим:

${\displaystyle e^{ix}=1+{\frac {ix}{1!}}+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+\ldots =\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots \right)+i\left({\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots \right)}$

Но

${\displaystyle 1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots =\cos x}$

${\displaystyle {\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots =\sin x}$

Поэтому ${\displaystyle e^{ix}=\cos x+i\sin x}$, что и требовалось доказать.

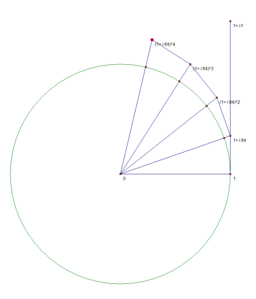
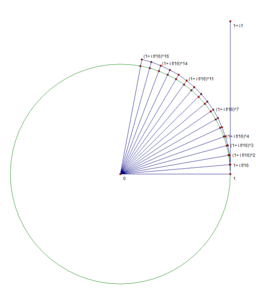
Наглядная демонстрация

Известно, что ${\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$. Нижеследующие изображения иллюстрируют, что предел ${\displaystyle e^{i\varphi }=\lim _{n\to \infty }\left(1+{\frac {i\varphi }{n}}\right)^{n}}$ равен точке, находящейся на единичной окружности, и длина дуги от этой точки до точки 1 равняется ${\displaystyle \varphi }$. Это, в частности, связано с тем, что ${\displaystyle \lim \limits _{x\to 0}{\frac {\sin x}{x}}=1}$.

• 
  n=1
• 
  n=2
• 
  n=3
• 
  n=4
• 
  n=5
• 
  n=6
• 
  n=8
• 
  n=16

Процесс изменения ${\displaystyle e^{\varphi i}}$ при изменении ${\displaystyle \varphi }$ можно также наглядно продемонстрировать через производную. Общеизвестно, что ${\displaystyle \left({e^{x}}\right)'=e^{x}}$ и ${\displaystyle \left({e^{f(x)}}\right)'=f'(x)e^{f(x)}}$. Этот же факт остаётся верным и для комплексного значения функции. Рассматривая функцию ${\displaystyle f(\varphi )=e^{\varphi i}}$, получим ${\displaystyle f'(\varphi )=if(\varphi )}$. Поскольку в геометрическом представлении комплексных чисел умножение на ${\displaystyle i}$ аналогично повороту на 90 градусов, то графическое изображение функции ${\displaystyle f(\varphi )=e^{\varphi i}}$ и её производной будет аналогично чертежу действия центростремительной силы, для которого известен физический смысл.

Показательная форма комплексного числа

Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.

Пусть комплексное число ${\displaystyle z}$ в тригонометрической форме имеет вид ${\displaystyle z=r(\cos \varphi +i\sin \varphi )}$ . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим:

${\displaystyle z=re^{i\varphi }}$

Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь ${\displaystyle r=|z|}$ , ${\displaystyle \varphi =\arg z}$.

Примечания

1. Cotes R. Logometria (англ.) // Philosophical Transactions of the Royal Society of London : journal. — 1714-1716. — Vol. 29. — P. 32. — doi:10.1098/rstl.1714.0002. Архивировано 6 июля 2017 года.
2. Cotes R. Harmonia mensurarum (неопр.). — 1722. — С. 28. Архивировано 7 июня 2020 года.
3. González-Velasco Enrique A. Journey through Mathematics: Creative Episodes in Its History (англ.). — 2011. — P. 182. Архивировано 19 октября 2014 года.
4. Euler L. Cap.VIII. De quantitatibus transcendentibus ex Circulo ortis // Introductio in analysin infinitorum (неопр.). — 1748. — Т. 1. — С. 104.

Литература

• Гутов А. З. Аналог формулы Эйлера для обобщённых синуса и косинуса // Современные методы физико-математических наук. Труды международной конференции. Орёл, 2006. С. 35—37. Архивная копия от 25 сентября 2020 на Wayback Machine
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
• Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — 530 с. Архивная копия от 7 июня 2015 на Wayback Machine