Параллелогон

Параллелого́н — многоугольник, замощающий пространство с использованием лишь параллельного переноса, при этом стороны параллелогонов совмещаются по целым сторонам^[1].

Стороны параллелогона это две или три пары равных параллельных отрезков. Вершины и рёбра внутри постороенного шестиугольника удаляются

Существует пять решёток Браве в двумерном пространстве, связанные с замощениями параллелогонами и их пятью вариантами симметрии

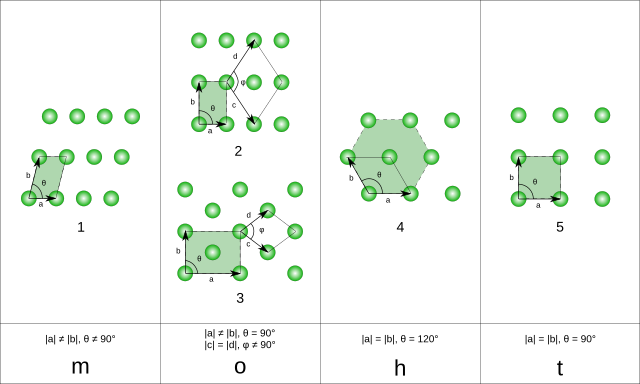
Параллелогон должен иметь чётное число сторон и противоположные стороны должны быть равны по длине и параллельны (согласно названию). Менее очевидное ограничение — параллелогон может иметь только четыре или шесть сторон^[1]. Четырёхсторонний параллелогон является параллелограммом. В общем случае параллелогон имеет вращательную симметрию на 180 градусов относительно центра.

Два типа

Четырёхугольные и шестиугольные параллелогоны имеют различные формы геометрической симметрии. В общем случае они имеют центральную симметрию с порядком 2. Шестиугольные параллелогоны могут быть невыпуклыми.

Число сторон	Примеры		Название	Симметрия и её порядок
4			Параллелограмм	Z2, порядок 2
			Прямоугольник & ромб	Dih2, порядок 4
			Квадрат	Dih4, порядок 8
6			Удлинённый параллелограмм	Z2, порядок 2
			Удлинённый ромб	Dih2, порядок 4
			Правильный шестиугольник	Dih6, порядок 12

Геометрические варианты

Параллелограммы могут замостить плоскость как деформированная квадратная мозаика, в то время как шестиугольные параллелогоны могут замостить плоскость как деформированная правильная шестиугольная мозаика.

Мозаика из параллелограммов

1 длина		2 длины
Прямой	Косой	Прямой	Косой
Квадрат p4m (*442)	Ромб cmm (2*22)	Прямоугольник pmm (*2222)	Параллелограмм p2 (2222)

Мозаика из шестиугольных параллелогонов

1 длина	2 длины		3 длины
Правильный шестиугольник p6m (*632)	Удлинённый ромб cmm (2*22)		Удлинённый параллелограмм p2 (2222)

См. также

• Параллелоэдр – обобщение параллелогона в трёхмерном пространстве