Независимое множество

Независимое множество в теории графов может быть как независимым множеством вершин, так и независимым множеством рёбер. Независимые множества рассматриваются в задачах покрытия графов.

Независимое множество из 9 голубых вершин

Независимое множество вершин

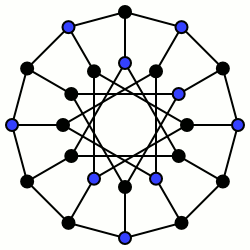
В неориентированном графе ${\displaystyle G=(V,E)}$ множество его вершин ${\displaystyle S}$, где ${\displaystyle S\subset V}$, называется независимым (или внутренне устойчивым), если любые две вершины в нем несмежны, то есть никакая пара вершин не соединена ребром ^{[1] [2] [3]}, или другими словами множество ${\displaystyle S}$ порождает пустой подграф:

${\displaystyle G(S,E^{\prime })\subset G~~\Rightarrow ~~E^{\prime }=\varnothing }$

Наибольшее число вершин в таких множествах называется вершинным числом независимости (иногда просто числом независимости) ${\displaystyle \beta _{0}(G)}$ графа ${\displaystyle G}$^[1], то есть, если ${\displaystyle Q}$ есть семейство всех независимых множеств вершин ${\displaystyle S}$, то ^[4] ${\displaystyle \beta _{0}(G)=\max\{|S|:S\in Q\}}$.

Независимое множество рёбер

В неориентированном графе ${\displaystyle G=(V,E)}$ множество его рёбер ${\displaystyle M}$, где ${\displaystyle M\subset E}$, называется независимым, если никакая пара ребер несмежна ^{[1] [3]} или множество ${\displaystyle M}$ порождает пустой подграф:

${\displaystyle G(V^{\prime },M)\subset G~~\Rightarrow ~~V^{\prime }=\varnothing }$

Наибольшее число рёбер в таких множествах называется рёберным числом независимости ${\displaystyle \beta _{1}(G)}$ графа ${\displaystyle G}$, то есть, если ${\displaystyle W}$ есть семейство всех независимых множеств рёбер ${\displaystyle M}$, то ${\displaystyle \beta _{1}(G)=\max\{|M|:M\in W\}}$.

Множество независимых рёбер также называют паросочетанием ^[5]. Поэтому независимое множество ${\displaystyle M}$, имеющее кардинальное число ${\displaystyle \beta _{1}}$ называется наибольшим паросочетанием графа ${\displaystyle G}$.

Примечания

1. Chartran, 2009, с. 98.
2. Кристофидес, 1978, с. 44.
3. Харари, 1973, с. 118.
4. Кристофидес, 1978, с. 45.
5. Харари, 1973, с. 119.

Литература

• Chartran G., Zhang P. Chromatic Graph Theory (англ.) / Series Editor Kenneth H. Rosen. — Baca Ration, London, New York: Chapman & Hall/CRC, 2009. — P. 483. — (Discrete Mathematics and Its Applications). — ISBN 978-1-58488-800-0.
• Кристофидес Н. Теория графов. Алгоритмический подход. (рус.). — М.: Мир, 1978. — 432 с.
• Харари Ф. Теория графов. (рус.). — М.: Мир, 1973. — 300 с.