The Fifty-Nine Icosahedra

The Fifty-Nine Icosahedra (în română Cele cincizeci și nouă de icosaedre) este o carte scrisă și ilustrată de H.S.M. Coxeter, P. Du Val, H.T. Flather și J.F. Petrie. Enumeră stelările icosaedrului regulat (convex, platonic), conform unui set de reguli propuse de J.C.P. Miller.

Diagrama de stelare a icosaedrului, cu triunghiul central marcat pentru icosaedrul originar

A fost publicată prima dată de Universitatea din Toronto în 1938, a urmat o a doua ediție de Springer-Verlag în 1982. A treia ediție, a lui Tarquin, din 1999 a inclus noi materiale de referință și fotografii de K. și D. Crennell.

Contribuțiile autorilor

Regulile lui Miller

Deși Miller nu a contribuit direct la carte, a fost un coleg apropiat al lui Coxeter și al lui Petrie. Contribuția sa este imortalizată în setul său de reguli pentru definirea formelor de stelate care ar trebui considerate „în mod corespunzător și distincte”:^[1]

(i) Fețele trebuie să se afle în douăzeci de plane, adică planele de delimitare ale icosaedrului regulat.

(ii) Toate părțile care compun fețele trebuie să fie aceleași în fiecare plan, deși pot fi destul de deconectate.

(iii) Părțile cuprinse în orice plan trebuie să aibă simetrie triunghiulară, cu sau fără reflexie. Acest lucru asigură simetria icosaedrică pentru întregul corp.

(iv) Părțile cuprinse în orice plan trebuie să fie toate „accesibile” în corpul completat (adică trebuie să fie în „exterior”. În anumite cazuri ar trebui să fie necesare modele de dimensiuni enorme pentru a vedea tot exteriorul). Cu un model de dimensiuni obișnuite, unele părți ale „exteriorului” ar putea fi explorate doar de o insectă târâtoare).

(v) Nu se iau în considerare cazurile în care părțile pot fi împărțite în două seturi, fiecare dând un corp cu la fel de multă simetrie ca întreaga figură. Dar se permite combinarea unei perechi enantiomorfe care nu au vreo parte comună (ceea ce de fapt apare într-un singur caz).

Regulile (i) până la (iii) sunt cerințe de simetrie pentru planele fețelor. Regula (iv) exclude găurile ascunse, ca să nu existe două stelări identice în exterior. Regula (v) previne orice compus format din stelări mai simple deconectate.

Coxeter

Coxeter a fost principala forță motrice din spatele lucrării. El a efectuat analiza originală pe baza regulilor lui Miller, adoptând o serie de tehnici precum combinatorica și teoria grafurilor abstractă a căror utilizare într-un context geometric a fost atunci inedită.

El a observat că diagrama de stelare cuprindea multe segmente. Apoi a dezvoltat proceduri pentru manipularea combinațiilor regiunilor din plane adiacente, pentru a enumera formal combinațiile permise de regulile lui Miller.

Graful său, reprodus alături, arată conectivitatea diferitelor fețe identificate în diagrama de stelare (vezi mai jos). Simbolurile grecești reprezintă seturi de alternative posibile:

λ poate fi 3 sau 4

μ poate fi 7 sau 8

ν poate fi 11 sau 12

Du Val

Du Val a conceput o notație simbolică pentru a identifica seturile de „celule” (a nu se confunda cu 3-față) congruente, pe baza observației că acestea se află în „straturi” (în original în „cochilii”) în jurul icosaedrului originar. Pe baza acestui fapt, el a testat toate combinațiile posibile conform regulilor lui Miller, confirmând rezultatul abordării mai analitice a lui Coxeter.

Flather

Contribuția lui Flather a fost indirectă: a făcut modele de carton pentru toate cele 59 de cazuri. Când l-a întâlnit prima dată pe Coxeter, el făcuse deja multe stelări, inclusiv câteva exemple care nu satisfăceau regulile lui Miller. El a continuat să realizeze toată seria de cincizeci și nouă de modele, care sunt păstrate în biblioteca matematică a Universității Cambridge. Biblioteca deține și câteva modele care nu satisfac regulile lui Miller, dar nu se știe dacă acestea au fost făcute de Flather sau de studenții de mai târziu ai lui Miller.^[2]

Petrie

John Flinders Petrie a fost un prieten de-o viață cu Coxeter și avea o abilitate remarcabilă în vizualizarea geometriei cvadridimensionale. El și Coxeter lucraseră împreună la multe probleme matematice. Contribuția sa directă la cele cincizeci și nouă de icosaedre a fost setul rafinat de desene tridimensionale care oferă o mare parte din fascinația lucrării publicate.

Kate și David Crennell

Pentru cea de-a treia ediție, Kate și David Crennell au revizuit textul și au redesenat figurile. Ei au adăugat și o secțiune de referință care conține tabele, diagrame și fotografii ale unora dintre modelele de la Cambridge (care la acea vreme erau considerate a fi ale lui Flather). Corecțiile aduse acestei ediții au fost publicate online.^[3]

Lista celor cincizeci și nouă de icosaedre

Diagrama de stelare cu seturile de fețe numerotate

Schema celulelor cu notația lui Du Val

Înainte de Coxeter, doar Brückner și Wheeler înregistraseră seturi semnificative de stelări, deși câteva, cum ar fi marele icosaedru, erau cunoscute de mai mult timp. De la publicarea lui The 59..., Wenninger a publicat instrucțiuni despre realizarea unor modele; schema de numerotare folosită în cartea sa a devenit larg folosită, deși el a descris doar câteva stelări.

Note privind lista

Dacă nu se specifică altfel, indexarea este după Crennell:

Crennell

• La indexarea numerotată adăugată ediției a treia de către Crennell, primele 32 de forme (indici 1–32) sunt forme cu simetrie de reflexie, iar ultimele 27 (indici 33–59) sunt forme chirale fiind enumerate doar formele pe dreapta. Lista folosește ordinea în care stelările sunt descrise în carte.

Celule

• În notația lui Du Val, fiecare strat este identificat cu caractere aldine, dinspre interior spre exterior: a, b, c, ..., h, unde a este icosaedrul originar. Unele straturi au două tipuri de celule, de exemplu, e se subdivide în e₁ și e₂. Setul f₁ se subdivide în continuare în forme pe dreapta și pe stânga, respectiv f₁ și f₁ (italic). În cazul în care o stelare are toate celulele prezente în interiorul unui strat exterior, stratul exterior este scris cu majuscule, iar cel interior este omis, de exemplu a + b + c + e₁ se scrie Ce₁.

Fețe

• Toate stelările pot fi descrise printr-o diagramă de stelare. În diagrama prezentată aici culorile numerotate indică regiunile diagramei de stelare care trebuie să apară împreună ca o mulțime dacă se dorește să se mențină simetria icosaedrică completă. Diagrama are 13 astfel de mulțimi. Unele dintre acestea se subdivid în perechi chirale (nu sunt prezentate), permițând stelări cu simetrie de rotație, dar nu și de reflexie. În tabel, fețele care sunt văzute de dedesubt sunt indicate printr-un apostrof, de exemplu 3'.

Wenninger

• Indecșii și numele numerotate au fost alocate arbitrar de către editorul lui Wenninger, în funcție de apariția lor în cartea sa „Modele poliedrice” și nu au nicio legătură cu niciun șir matematic. Doar câteva dintre modelele sale erau de icosaedre. La el numele sunt date sub formă scurtă, „... a icosaedrului”.

Wheeler

• Wheeler și-a găsit figurile, sau „formele” icosaedrului, alegând segmente de dreaptă din diagrama de stelare. El a distins cu atenție acest lucru de procesul clasic de stelare al lui Kepler. Coxeter și colaboratorii săi au ignorat această distincție și s-au referit la toate drept stelări.

Brückner

• Max Brückner a realizat și fotografiat modele ale multor poliedre, dintre care doar câteva erau icosaedre. Taf. este o abreviere a lui Tafel („tabel”) din germană.

Observații

• Nr. 8 este uneori numit echidnaedru după o asemănare imaginară cu furnicarul spinos sau cu echidna. Această utilizare este independentă de descrierea de către Kepler a poliedrelor regulate stelate ca „echidnele” sale.

Tabelul celor cincizeci și nouă de icosaedre

Unele imagini ilustrează icosaedrul imaginii în oglindă, cu celula f₁ în loc de celula f₁.

Crennell	Celule	Fețe	Wenninger	Wheeler	Brückner	Observații	Diagrama feței	În 3D
1	A	0	04 Icosaedru	1	9999 	Icosaedrul Platonic
2	B	1	26 Icosaedru triakis	2	0802 Taf. VIII, Fig. 2	Prima stelare a icosaedrului, micul icosaedru triambic
3	C	2	23 Compus de cinci octaedre	3	0906 Taf. IX, Fig. 6	Compus de cinci octaedre regulat
4	D	3 4	0	4	0917 Taf. IX, Fig.17
5	E	5 6 7	0	0	9999 
6	F	8 9 10	27 A doua stelare	19	9999 	A doua stelare a icosaedrului
7	G	11 12	41 Marele icosaedru	11	1124 Taf. XI, Fig. 24	Marele icosaedru
8	H	13	42 Stelarea finală	12	1114 Taf. XI, Fig. 14	Stelarea finală a icosaedrului sau Echidnaedru
9	e1	3' 5	37 A douăsprezecea stelare	0	9999 	A douăsprezecea stelare a icosaedrului
10	f1	5' 6' 9 10	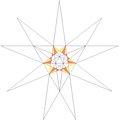0	0	9999 
11	g1	10' 12	29 A patra stelare	21	9999 	A patra stelare a icosaedrului
12	e1f1	3' 6' 9 10	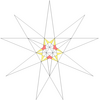0	0	9999 
13	e1f1g1	3' 6' 9 12	0	20	9999 
14	f1g1	5' 6' 9 12	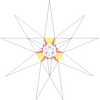0	0	9999 
15	e2	4' 6 7	0	0	9999 
16	f2	7' 8	0	22	9999 
17	g2	8' 9'11	0	0	9999 
18	e2f2	4' 6 8	0	0	9999 
19	e2f2g2	4' 6 9' 11	0	0	9999 
20	f2g2	7' 9' 11	30 A cincea stelare	0	9999 	A cincea stelare a icosaedrului
21	De1	4 5	32 A șaptea stelare	10	9999 	A șaptea stelare a icosaedrului
22	Ef1	7 9 10	25 Compus de zece tetraedre	8	0903 Taf. IX, Fig. 3	Compus de zece tetraedre regulat
23	Fg1	8 9 12	31 A șasea stelare	17	1003 Taf. X, Fig. 3	A șasea stelare a icosaedrului
24	De1f1	4 6' 9 10	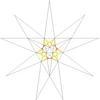0	0	9999 
25	De1f1g1	4 6' 9 12	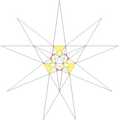0	0	9999 
26	Ef1g1	7 9 12	28 A treia stelare	9	0826 Taf. VIII, Fig. 26	Dodecaedru excavat
27	De2	3 6 7	0	5	9999 
28	Ef2	5 6 8	0	18	0920 Taf.IX, Fig. 20
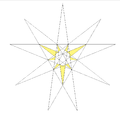29	Fg2	10 11	33 A opta stelare	14	9999 	A opta stelare a icosaedrului
30	De2f2	3 6 8	34 A noua stelare	13	9999 	Icosaedru triambic medial sau Marele icosaedru triambic
31	De2f2g2	3 6 9' 11	0	0	9999 
32	Ef2g2	5 6 9' 11	0	0	9999 
33	f1	5' 6' 9 10	35 A zecea stelare	0	9999 	A zecea stelare a icosaedrului
34	e1f1	3' 5 6' 9 10	36 A unsprezecea stelare	0	9999 	A unsprezecea stelare a icosaedrului
35	De1f1	4 5 6' 9 10	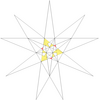0	0	9999 
36	f1g1	5' 6' 9 10' 12	0	0	9999 
37	e1f1g1	3' 5 6' 9 10' 12	39 A paisprezecea stelare	0	9999 	A paisprezecea stelare a icosaedrului
38	De1f1g1	4 5 6' 9 10' 12	0	0	9999 
39	f1g2	5' 6' 8' 9' 10 11	0	0	9999 
40	e1f1g2	3' 5 6' 8' 9' 10 11	0	0	9999 
41	De1f1g2	4 5 6' 8' 9' 10 11	0	0	9999 
42	f1f2g2	5' 6' 7' 9' 10 11	0	0	9999 
43	e1f1f2g2	3' 5 6' 7' 9' 10 11	0	0	9999 
44	De1f1f2g2	4 5 6' 7' 9' 10 11	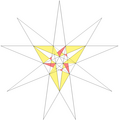0	0	9999 
45	e2f1	4' 5' 6 7 9 10	40 A cincisprezecea stelare	0	9999 	A cincisprezecea stelare a icosaedrului
46	De2f1	3 5' 6 7 9 10	0	0	9999 
47	Ef1	5 6 7 9 10	24 Compus de cinci tetraedre	7 (6: pe stânga)	0911 Taf. IX, Fig. 11	Compus de cinci tetraedre (pe dreapta)
48	e2f1g1	4' 5' 6 7 9 10' 12	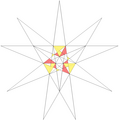0	0	9999 
49	De2f1g1	3 5' 6 7 9 10' 12	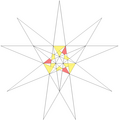0	0	9999 
50	Ef1g1	5 6 7 9 10' 12	0	0	9999 
51	e2f1f2	4' 5' 6 8 9 10	38 A treisprezecea stelare	0	9999 	A treisprezecea stelare a icosaedrului
52	De2f1f2	3 5' 6 8 9 10	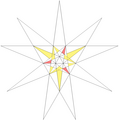0	0	9999 
53	Ef1f2	5 6 8 9 10	0	15 (16: pe stânga)	9999 
54	e2f1f2g1	4' 5' 6 8 9 10' 12	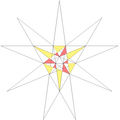0	0	9999 
55	De2f1f2g1	3 5' 6 8 9 10' 12	0	0	9999 
56	Ef1f2g1	5 6 8 9 10' 12	0	0	9999 
57	e2f1f2g2	4' 5' 6 9' 10 11	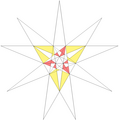0	0	9999 
58	De2f1f2g2	3 5' 6 9' 10 11	0	0	9999 
59	Ef1f2g2	5 6 9' 10 11	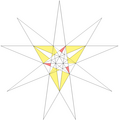0	0	9999 

Note

1. Coxeter, du Val ș.a., 1999, p. 15–16
2. en Inchbald, G., Some lost stellations of the icosahedron, steelpillow.com, 11 July 2006. Retrieved 14 September 2017)
3. en K. și D. Crennell, The Fifty-Nine Icosahedra, Fortran Friends. Retrieved 14 September 2017.

Bibliografie

• en Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte. Leipzig: B.G. Treubner. ISBN: 978-1-4181-6590-1.

WorldCat English: Polygons and Polyhedra: Theory and History. Photographs of models: Tafel VIII (Plate VIII), etc. High res. scans.

• en H.S.M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26.
  • en Third edition (1999) Tarquin ISBN: 978-1-899618-32-3 marathi {{{1}}}
• en Wenninger, Magnus J. (1983) Polyhedron models; Cambridge University Press, Paperback edition (2003). ISBN: 978-0-521-09859-5.
• en A.H. Wheeler (1924) "Certain forms of the icosahedron and a method for deriving and designating higher polyhedra", Proceedings of the International Congress of Mathematicians, Toronto, Vol. 1, pp 701–708.

Legături externe

• en Example stellations of the icosahedron
• en The fifty nine stellations of the regular icosahedron
• en Eric W. Weisstein, Fifty nine icosahedron stellations la MathWorld.
  • en Eric W. Weisstein, Echidnahedron la MathWorld.
• en Stellations of the icosahedron

	Portal matematică

• en George Hart, 59 Stellations of the Icosahedron - VRML 3D files.

Selecție din cele 59 de posibile stelări ale icosaedrului
Regulat	Duale ale uniformelor		Compuși regulați			Stelare regulată	Altele
Icosaedru (convex)	Micul icosaedru triambic	Marele icosaedru triambic	Compus de cinci octaedre	Compus de cinci tetraedre	Compus de zece tetraedre	Marele icosaedru	Dodecaedru excavat	Stelarea finală
Procesul de stelare al icosaedrului creează un număr de poliedre și compuși înrudiți, cu simetrie icosaedrică.