Remove ads
În matematică, o categorie (numită uneori categorie abstractă pentru a o deosebi de o categorie concretă(d)) este o colecție de „obiecte” care sunt legate prin „săgeți”. O categorie are două proprietăți de bază: capacitatea de a compune săgeți asociativ și existența unei săgeți identitate pentru fiecare obiect. Un exemplu simplu este categoria mulțimilor(d), ale căror obiecte sunt mulțimi și ale căror săgeți sunt funcții.
Teoria categoriilor este o ramură a matematicii care încearcă să generalizeze toată matematica în termeni de categorii, indiferent ce reprezintă obiectele și săgețile lor. Practic orice ramură a matematicii moderne poate fi descrisă în termeni de categorii, și această reprezentare dezvăluie adesea aspecte și similitudini profunde între domenii aparent diferite ale matematicii. Ca atare, teoria categoriilor furnizează un fundament alternativ al matematicii față de teoria mulțimilor și alte fundamente axiomatice propuse. În general, obiectele și săgețile pot fi entități abstracte de orice fel, iar noțiunea de categorie furnizează o modalitate fundamentală și abstractă de a descrie entitățile matematice și relațiile între ele.
Pe lângă formalizarea matematicii, teoria categoriilor este folosită și pentru a formaliza multe alte sisteme în informatică, cum ar fi semantica limbajelor de programare(d).
Două categorii sunt identice dacă au aceeași colecție de obiecte, aceeași colecție de săgeți, și aceeași metodă asociativă de compunere a oricărei perechi de săgeți. Două categorii diferite pot fi considerate și ele „echivalente(d)” în contextul teoriei categoriilor, chiar dacă nu au exact aceeași structură.
Categoriile cunoscute se notează cu un cuvânt scurt cu inițială majusculă sau cu o abreviere scrisă cu aldine sau italice: printre exemple se numără Set(d), categoria mulțimilor și funcțiilor definite pe mulțimi; Ring(d), categoria inelelor și omomorfismelor de inel(d); și Top(d), categoria spațiilor topologice și a aplicațiilor continue. Toate aceste categorii au aplicația identitate drept săgeată identitate și compunerea(d) ca operație asociativă pe săgeți.
Remove ads
Teoria categoriilor a apărut pentru prima oară într-un articol intitulat „General Theory of Natural Equivalences”, scris de Samuel Eilenberg și Saunders Mac Lane(d) în 1945.[1]
Există mai multe definiții echivalente pentru o categorie.[2] Una frecvent folosită este după cum urmează. O categorie C constă din
- o clasă ob(C) de obiecte
- o clasă hom(C) de morfisme, sau săgeți, sau aplicații, între obiecte. Fiecare morfism f are un obiect sursă a și un obiect destinație b unde a și b sunt din ob(C). Scrieme f: a → b, și spunem „f este un morfism de la a la b”. Scriem hom(a, b) (sau homC(a, b) atunci când ar putea apărea confuzii despre categoria la care se referă hom(a, b)) pentru a nota hom-clasa tuturor morfismelor de la a la b. (Unii autori scriu Mor(a, b) sau pur și simplu C(a, b).)
- pentru oricare trei obiecte a, b și c, o operație binară hom(a, b) × hom(b, c) → hom(a, c) numită compoziție de morfisme; compoziția lui f : a → b și g : b → c este notată cu g ∘ f sau gf. (Unii autori folosesc „ordinea diagramatică”, scriind f;g sau fg.)
astfel încât sunt valabile următoarele axiome:
- (asociativitatea) dacă f : a → b, g : b → c și h : c → d atunci h ∘ (g ∘ f) = (h ∘ g) ∘ f, și
- (identitatea(d)) pentru orice obiect x, există un morfism 1x : x → x (unii autori îl notează cu idx) numit morfismul identitate pentru x, astfel încât pentru orice morfism f : a → x și orice morfism g : x → b, avem 1x ∘ f = f și g ∘ 1x = g.
Din aceste axiome, se poate demonstra că există exact un singur morfism identitate pentru fiecare obiect. Unii autori folosesc o variație a definiției în care fiecare obiect este identificat cu morfismul său identitate corespunzător.
Remove ads
O categorie C se numește mică dacă atât ob(C) cât și hom(C) sunt de fapt mulțimi și nu clase proprii, și mare altfel. O categorie local mică este o categorie astfel încât pentru toate obiectele a și b, hom-clasa hom(a, b) este o mulțime, numită homulțime. Multe categorii importante din matematică (cum ar fi categoria mulțimilor), deși nu sunt mici, sunt cel puțin local mici. Întrucât, la categoriile mici, obiectele formează o mulțime, o categorie mică poate fi văzută ca o structură algebrică similară cu un grup dar fără proprietățile de element simetric sau închidere. Categoriile mari, pe de altă parte, pot fi folosite pentru a crea „structuri” din structuri algebrice.
Remove ads
Clasa tuturor mulțimilor (ca obiecte) împreună cu toate funcțiile între ele (ca morfisme), unde compunerea de morfisme este compunerea uzuală a funcțiilor(d), formează o categorie mare, Set(d). Este cea mai elementară și mai frecvent utilizată categorie din matematică. Categoria Rel(d) constă din toate mulțimile (ca obiecte) cu relații binare între ele (ca morfisme). Abstractizarea de la relații în loc de funcții produce alegorii(d), o clasă specială de categorii.
Orice clasă poate fi văzută ca o categorie ale cărei morfisme sunt morfismele identitate. Astfel de categorii sunt numite discrete(d). Pentru orice mulțime I dată, categoria discretă pe I este categoria mică cu elementele lui I ca obiecte și cu morfismele identitate ca morfisme. Categoriile discrete sunt cel mai simplu fel de categorie.
Orice mulțime preordonată(d) (P, ≤) formează o categorie mică, ale cărei obiecte sunt membrii lui P, și ale cărei morfisme sunt săgeți care arată de la x la y când x ≤ y. Mai mult, dacă ≤ este antisimetrică(d), poate exista cel mult un singur morfism între oricare două obiecte. Existența morfismelor identitate și compunabilitatea morfismelor sunt garantate de reflexivitatea(d) și tranzitivitatea(d) relației de preordine. Conform aceluiași argument, orice mulțime parțial ordonată(d) și orice relație de echivalență poate fi văzută ca o categorie mică. Orice număr ordinal poate fi privit ca o categorie atunci când este văzut ca o mulțime ordonată.
Orice monoid (orice structură algebrică cu o singură operație binară asociativă și cu un element identic) formează o categorie mică cu un singur obiect x. (Aici, x este orice mulțime fixă.) Morfismele de la x la x sunt exact elementele monoidului, morfismul identitate al lui x este identitatea monoidului, și compunerea caracteristică a morfismelor este dată de operația monoidului. Mai multe definiții și teoreme despre monoizi pot fi generalizate pentru categorii.
Analog, orice grup poate fi privit ca o categorie cu un singur obiect în care toate morfismele sunt inversabile, adică pentru orice morfism f există un morfism g care este invers la stânga și la dreapta pentru f în raport cu compunerea. Un morfism inversabil în acest sens este numit izomorfism.
Un grupoid(d) este o categorie în care toate morfismele sunt izomorfisme. Grupoizii sunt generalizări ale grupurilor, acțiunilor de grup(d) și relațiilor de echivalență.
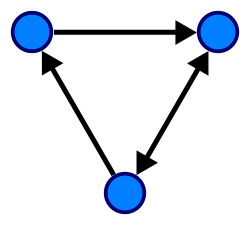
Orice graf orientat generează(d) o categorie mică: obiectele sunt nodurile grafului, iar morfismele sunt drumuri în graf (dotate cu bucle(d) după nevoie) în care compunerea morfismelor este concatenarea drumurilor. O astfel de categorie se numește categoria liberă(d) generată de graf.
Clasa tuturor mulțimilor preordonate cu funcțiile monotone ca morfisme formează o categorie, Ord(d). Ea este o categorie concretă(d) adică o categorie obținută prin adăugarea unui tip de structură la Set, și punând condiția ca morfismele să fie funcții care respectă această structură adăugată.
Clasa tuturor grupurilor cu omomorfismele de grup ca morfisme și compunerea funcțiilor(d) ca operație de compunere formează o categorie mare, Grp(d). Ca și Ord, Grp este o categorie concretă. Categoria Ab(d), constând din toate grupurile abeliene și omomorfismele lor de grup, este o subcategorie completă(d) a lui Grp, și prototipul unei categorii abeliene(d). Alte exemple de categorii concrete sunt date în tabelul următor.
| Categorie | Obiecte | Morfisme |
|---|---|---|
| Mag(d) | magme(d) | omomorfisme de magmă(d) |
| Manp(d) | varietăți derivabile(d) | aplicații derivabile de p ori cu derivata continuă |
| Met(d) | spații metrice | funcții neexpansive(d) |
| R-Mod(d) | R-module(d), unde R este un inel | omomorfisme de R-modul(d) |
| Ring(d) | inelele | omomorfisme de inel(d) |
| Set(d) | mulțimile | funcții |
| Grp(d) | grupuri | omomorfisme de grup |
| Top(d) | spații topologice | funcții continue |
| Uni(d) | spații uniforme(d) | funcții uniform continue |
| VectK(d) | spații vectoriale peste corpul K | aplicații liniare peste K |
Categoria Cat(d) constă din toate categoriile mici, cu functorii dintre ele ca morfisme.
Remove ads
Categorie duală
Orice categorie C poate fi considerată o categorie nouă într-un fel diferit: obiectele sunt aceleași ca cele din categoria originară, dar săgețile sunt cele ale categoriei originare, dar inversate. Aceasta se numește categoria duală sau opusă(d) și se notează cu Cop.
Categoriile produs
Dacă C și D sunt categorii, se poate forma categoria produs C × D: obiectele sunt perechi formate dintr-un obiect din C și unul din D, iar morfismele sunt tot perechi, constând dintr-un morfism din C și unul din D. Asemenea perechi pot fi compuse pe componente(d).
Remove ads
Un morfism f : a → b se numește
- monomorfism(d) (sau monic) dacă este anulabil la stânga, adică. fg1 = fg2 implică g1 = g2 pentru orice morfisme g1, g2 : x → a.
- un epimorfism(d) (sau epic) este anulabil la dreapta, adică g1f = g2f implică g1 = g2 pentru orice morfisme g1, g2 : b → x.
- un bimorfism este un monomorfism care este și epimorfism.
- o retracție(d) dacă are inversă la dreapta, adică dacă există un morfism g : b → a cu fg = 1b.
- o secțiune(d) dacă are o inversă la stânga, adică există un morfism g : b → a cu gf = 1a.
- un izomorfism dacă are o inversă, adică dacă există un morfism g : b → a cu fg = 1b și gf = 1a.
- un endomorfism(d) dacă a = b. Clasa endomorfismelor lui a se notează cu end(a).
- un automorfism dacă f este și endomorfism și izomorfism. Clasa automorfismelor lui a se notează cu aut(a).
Orice retracție este un epimorfism. Orice secțiune este un monomorfism. Următoarele trei afirmații sunt echivalente:
- f este un monomorfism și o retracție;
- f este un epimorfism și o secțiune;
- f este un izomorfism.
Relațiile între morfisme (cum ar fi fg = h) pot fi reprezentate cel mai convenabil prin diagrame comutative(d), în care obiectele sunt reprezentate ca puncte și morfismele ca săgeți.
Remove ads
- În multe categorii, de exemplu Ab(d) sau VectK(d), homulțimile hom(a, b) sunt nu doar mulțimi, ci chiar grupuri abeliene, și compunerea morfismelor este compatibilă cu aceste structuri de grup; adică este biliniară. O astfel de categorie se numește preaditivă(d). Dacă, mai mult, categoria are numai produse(d) și coproduse(d) finite, se numește categorie aditivă(d). Dacă toate morfismele au un nucleu(d) și un conucleu(d), și toate epimorfismele sunt conuclee și toate monomorfismele sunt nuclee, atunci este vorba de o categorie abeliană(d). Un exemplu tipic de categorie abeliană este categoria grupurilor abeliene.
- O categorie se numește completă(d) dacă toate limitele(d) mici există în ea. Categoria mulțimilor, grupurilor abeliene și spațiilor topologice sunt complete.
- O categorie se numește cartezian închisă(d) dacă are produse directe finite și un morfism definit pe un produs finit poate fi mereu reprezentat de un morfism definit doar pe unul din factori. Printre exemple se numără Set(d) și CPO, categoria relațiilor de ordine parțiale complete(d) cu funcții Scott-continue(d).
- Un topos(d) este un anume tip de categorie cartezian închisă în care se poate formula toată matematica (așa cum, clasic, toată matematica este formulată categoria mulțimilor). Un topos poate fi folosit și pentru a reprezenta o teorie logică.
Remove ads
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads