Inverso multiplicativo

Em matemática, o inverso multiplicativo de um número x é o número y que, multiplicado por x, gera a identidade multiplicativa. Note-se que estamos falando de qualquer operação binária que tenha o nome de multiplicação, que não precisa ser comutativa, mas deve ter elemento neutro.

A função real de variável real f(x)=1/x asoccia cada x não-nulo com seu inverso multiplicativo.

No caso de uma operação não comutativa, o inverso deve ser tal que ${\displaystyle x\times y=y\times x=1}$.

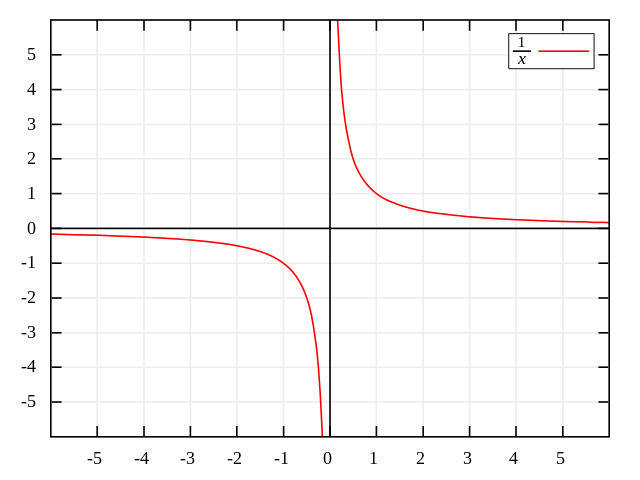
Quando este inverso é único (por exemplo, o inverso multiplicativo de um número real), ele é representado por:

${\displaystyle 1\div y={\frac {1}{y}}=y^{(-1)}={\sqrt[{(-1)}]{y}}}$

ou

${\displaystyle m^{w}={\sqrt[{\frac {1}{w}}]{m}}}$

ou

${\displaystyle a^{\frac {1}{c}}={\sqrt[{c}]{a}}}$

O termo "recíproco" era de uso comum pelo menos até a terceira edição de "Encyclopædia Britannica" (1797) para descrever dois números cujo produto é 1; As quantidades geométricas em proporção inversa são descritas como reciprocall em uma tradução 1570 de Euclid Elements .^[1]

Unicidade

As condições necessárias para que se possa definir o inverso multiplicativo são um conjunto S, uma operação binária * definida como uma função ${\displaystyle \star :S\times S\to S}$ e a existência de um elemento neutro 1 desta operação, definido de forma que ${\displaystyle \forall x\in S,1\times x=x\times 1=x}$.

Estas são as definições de um grupóide com elemento neutro.

Por exemplo, para a operação binária × definida no conjunto {1, a, b, c} de forma que 1 seja o elemento neutro, a × a = 1, a × b = 1, a × c = a, b × a = 1, b × b = b, b × c = b, c × a = c, c × b = 1 e c × c = c, temos que a é um elemento inverso de a, b também é um elemento inverso de a e a é um elemento inverso de b, e não existe elemento inverso de c. Note-se que no caso geral, o elemento inverso não precisa existir nem ser único (devia se chamar de um elemento inverso, em vez de o elemento inverso).

Quando a operação é associativa (ou seja, (S, *) é um monóide), pode-se mostrar que o inverso, se existe, é único:

Seja x um elemento de S, e y e z elementos inversos de x. Então, pela associatividade:

${\displaystyle (z\times x)\times y=z\times (x\times y)}$

Portanto, pelas definições de elemento inverso e de elemento neutro:

${\displaystyle 1\times y=z\times 1}$

${\displaystyle y=z}$

Inverso multiplicativo de alguns números

número	valor inverso
0	${\displaystyle {\infty }}$
1	${\displaystyle 1}$
2	${\displaystyle 0,5}$
3	${\displaystyle 0,{\overline {3}}}$
4	${\displaystyle 0,25}$
5	${\displaystyle 0,2}$
6	${\displaystyle 0,1{\overline {6}}}$
7	${\displaystyle 0,{\overline {142857}}}$
8	${\displaystyle 0,125}$
9	${\displaystyle 0,{\overline {1}}}$
10	${\displaystyle 0,1}$
11	${\displaystyle 0,{\overline {09}}}$
12	${\displaystyle 0,08{\overline {3}}}$
13	${\displaystyle 0,{\overline {076923}}}$
14	${\displaystyle 0,0{\overline {714285}}}$
15	${\displaystyle 0,0{\overline {6}}}$
16	${\displaystyle 0,0625}$
17	${\displaystyle 0,{\overline {0588235294117647}}}$
18	${\displaystyle 0,0{\overline {5}}}$
19	${\displaystyle 0,{\overline {052631578947368421}}}$
20	${\displaystyle 0,05}$

Em forma de divisão

O resultado de ${\displaystyle A\div B}$ é o inverso do resultado de ${\displaystyle B\div A}$. Ou seja, para descobrir o valor inverso de um número que é resultado de uma divisão, é só trocar o dividendo e o divisor de lugar. Exemplos:

• Se ${\displaystyle 16\div 4=4}$, para descobrir o valor inverso de 4, é só trocar o dividendo e o divisor de lugar, que vai ser ${\displaystyle 4\div 16=0,25}$. Portanto, 0,25 é o valor inverso de 4.
• Se ${\displaystyle 15\div 3=5}$, para descobrir o valor inverso de 5, é só trocar o dividendo e o divisor de lugar, que vai ser ${\displaystyle 3\div 15=0,2}$. Portanto, 0,2 é o valor inverso de 5.
• Se ${\displaystyle 72\div 9=8}$, para descobrir o valor inverso de 8, é só trocar o dividendo e o divisor de lugar, que vai ser ${\displaystyle 9\div 72=0,125}$. Portanto, 0,125 é o valor inverso de 8.
• Se ${\displaystyle 100\div 10=10}$, para descobrir o valor inverso de 10, é só trocar o dividendo e o divisor de lugar, que vai ser ${\displaystyle 10\div 100=0,1}$. Portanto, 0,1 é o valor inverso de 10.

Em forma de potenciação

O resultado de ${\displaystyle A^{B}}$ é o inverso do resultado de ${\displaystyle A^{(-B)}}$. Ou seja, para descobrir o valor inverso de um número que é resultado de uma potenciação, é só conservar a base e trocar o expoente de positivo para negativo, ou de negativo para positivo. Exemplos:

• Se ${\displaystyle 2^{2}=4}$, para descobrir o valor inverso de 4, é só trocar o expoente positivo para negativo, que vai ser ${\displaystyle 2^{(-2)}=0,25}$. Portanto, 0,25 é o valor inverso de 4.
• Se ${\displaystyle 3^{3}=27}$, para descobrir o valor inverso de 27, é só trocar o expoente positivo para negativo, que vai ser ${\displaystyle 3^{(-3)}=0,{\overline {037}}}$. Portanto, a dízima periódica ${\displaystyle 0,{\overline {037}}}$ é o valor inverso de 27.
• Se ${\displaystyle 5^{5}=3125}$, para descobrir o valor inverso de 3125, é só trocar o expoente positivo para negativo, que vai ser ${\displaystyle 5^{(-5)}=0,00032}$. Portanto, 0,00032 é o valor inverso de 3125.
• Se ${\displaystyle 10^{6}=1000000}$, para descobrir o valor inverso de 1000000, é só trocar o expoente positivo para negativo, que vai ser ${\displaystyle 10^{(-6)}=0,000001}$. Portanto, 0,000001 é o valor inverso de 1000000.

Em forma de radiciação

O resultado de ${\displaystyle {\sqrt[{Q}]{W}}}$ é o inverso do resultado de ${\displaystyle {\sqrt[{(-Q)}]{W}}}$. Ou seja, para descobrir o valor inverso de um número que é resultado de uma potenciação, é só conservar o radicando e trocar o índice de positivo para negativo, ou de negativo para positivo. Exemplos:

• Se ${\displaystyle {\sqrt[{12}]{8916100448256}}=12}$, para descobrir o valor inverso de 12, é só índice o expoente positivo para negativo, que vai ser ${\displaystyle {\sqrt[{(-12)}]{8916100448256}}=0,08{\overline {3}}}$. Portanto, a dízima periódica ${\displaystyle 0,08{\overline {3}}}$ é o valor inverso de 12.
• Se ${\displaystyle {\sqrt[{8}]{16777216}}=8}$, para descobrir o valor inverso de 8, é só trocar o índice positivo para negativo, que vai ser ${\displaystyle {\sqrt[{(-8)}]{16777216}}=0,125}$. Portanto, 0,125 é o valor inverso de 8.
• Se ${\displaystyle {\sqrt[{7}]{823543}}=7}$, para descobrir o valor inverso de 7, é só trocar o índice positivo para negativo, que vai ser ${\displaystyle {\sqrt[{(-7)}]{823543}}=0,{\overline {142857}}}$. Portanto, a dízima periódica ${\displaystyle 0,{\overline {142857}}}$ é o valor inverso de 7.
• Se ${\displaystyle {\sqrt[{5}]{3125}}=5}$, para descobrir o valor inverso de 5, é só trocar o índice positivo para negativo, que vai ser ${\displaystyle {\sqrt[{(-5)}]{3125}}=0,2}$. Portanto, 0,2 é o valor inverso de 5.

Referências

1. "In equall Parallelipipedons the bases are reciprokall to their altitudes". OED "Reciprocal" §3a. Sir Henry Billingsley translation of Elements XI, 34.