Declive

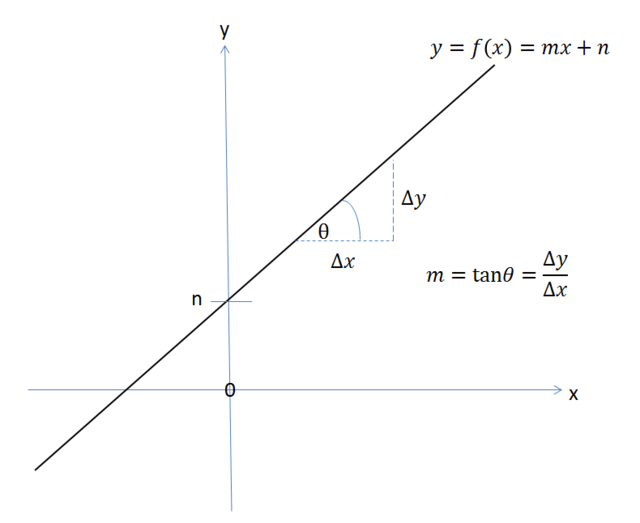
Em matemática, o declive, também chamado de coeficiente angular, é a medida relacionada à inclinação de uma reta face ao eixo horizontal. Coincide numericamente com a tangente do ângulo de inclinação, formado entre a reta e esse eixo. Dada uma reta representada por ${\displaystyle y=mx+n}$, diz-se que ${\displaystyle m}$ representa o seu declive.^[1][2][3]

Gráfico de uma função do primeiro grau, caracterizado por uma reta. O coeficiente angular da reta é geralmente representado pela letra "m".

Condições

É possível determinar o comportamento da reta ${\displaystyle y=f(x)}$ nas seguintes condições:

• Se ${\displaystyle m>0}$, a reta é dita crescente, pois ${\displaystyle \lim _{x\rightarrow +\infty }f(x)=+\infty }$.
• Se ${\displaystyle m<0}$, a reta é dita decrescente, pois conforme ${\displaystyle \lim _{x\rightarrow +\infty }f(x)=-\infty }$.
• Se ${\displaystyle m=0}$, a inclinação é nula em relação ao eixo horizontal e a função que a reta representa é dita constante, pois ${\displaystyle \lim _{x\rightarrow +\infty }f(x)=k}$, onde ${\displaystyle k}$ é uma constante real.

No caso em que ${\displaystyle m=\tan {\Bigl (}{\frac {\pi }{2}}{\Bigl )}}$, temos uma reta vertical, definida como Falhou a verificação gramatical (SVG (MathML pode ser ativado através de uma extensão do ''browser''): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "http://localhost:6011/pt.wikipedia.org/v1/":): {\displaystyle x=k} , onde ${\displaystyle k}$ é uma constante real.

Definição

Seja ${\displaystyle \theta }$ um ângulo arbitrário formado entre a reta ${\displaystyle y=mx+n}$ e o eixo das abscissas e ${\displaystyle (x_{0},\ y_{0})}$ e ${\displaystyle (x,\ y)}$ dois pontos pertencentes à essa reta, o coeficiente angular ${\displaystyle m}$ é definido como^[2]:

${\displaystyle m=\tan \theta ={\frac {y-y_{0}}{x-x_{0}}}={\frac {\Delta y}{\Delta x}}}$

Declive de uma curva

Ver artigo principal: Derivada

Dada a curva ${\displaystyle \mathrm {C} :y=f(x)}$, seu declive no ponto ${\displaystyle (x,\ f(x))}$ é dado pela derivada ${\displaystyle f'(x)}$, i.e. a inclinação da reta tangente no ponto considerado.^[1]

A derivada da função em um ponto arbitrário define o declive da reta tangente àquele ponto.

Equação fundamental da reta

A equação fundamental da reta é uma das três formas básicas da equação do primeiro grau (junto à equação reduzida e equação geral). Essa forma permite o cálculo de qualquer ponto ${\displaystyle (x,\ y)}$ da reta apenas sabendo seu coeficiente angular e um ponto ${\displaystyle (x_{0},\ y_{0})}$ definido. É obtida a partir da definição do coeficiente angular^[4]:

${\displaystyle m={\frac {y-y_{0}}{x-x_{0}}}}$

Multiplicando ambos os lados por ${\displaystyle (x-x_{0})}$, obtemos a equação fundamental da reta:

${\displaystyle y-y_{0}=m(x-x_{0})}$

Referências

1. «declive de uma reta». Infopédia (em linha). Porto: Porto Editora. 2003–2011
2. SILVA, Marcos Noé Pedro (2019). «Cálculo do coeficiente angular de uma reta». Brasil Escola. Consultado em 9 de setembro de 2020
3. LUZ, Ana Maria (Janeiro de 2001). «UNIDADE 1 - Matemática para Economia 1: Revisão de função de uma variável real» (PDF). Universidade Federal Fluminense - Departamento de Análise. Consultado em 9 de setembro de 2020
4. SILVA, Marcos Noé Pedro (2019). «Equação Fundamental da Reta». Brasil Escola. Consultado em 9 de setembro de 2020