Loading AI tools
Szereg Fouriera – szereg pozwalający rozłożyć funkcję okresową[1] lub nieokresową[2], spełniającą warunki Dirichleta, na sumę funkcji trygonometrycznych. Szeregi Fouriera zostały wprowadzone w 1807 roku przez Josepha Fouriera w celu rozwiązania równania przewodnictwa ciepła dla metalowej płyty. Równanie to jest równaniem różniczkowym cząstkowym i nie da się go rozwiązać bezpośrednio dla większości funkcji; jednak rozkładając funkcję początkową na szereg Fourier łatwo znalazł rozwiązania równania przewodnictwa dla poszczególnych składowych harmonicznych, ponieważ pochodne funkcji trygonometrycznych dają proste wzory, a następnie obliczył rozwiązanie dla funkcji wejściowej, sumując rozwiązania dla jej składowych harmonicznych. W 1829 r. Dirichlet określił ściśle warunki, jakie muszą spełniać funkcje, by szereg Fouriera był do nich zbieżny.
Szeregi Fouriera są np. ściśle powiązane z transformatą Fouriera, odkrytą przez Fouriera, którą można wykorzystać do znalezienia informacji o częstotliwościach składowych funkcji nieokresowych.
Od czasów Fouriera odkryto wiele różnych podejść do definiowania i rozumienia szeregu Fouriera. Niektóre z bardziej wydajnych i eleganckich podejść opierają się na pomysłach i narzędziach matematycznych, które nie były dostępne w czasach Fouriera. Fourier pierwotnie zdefiniował szereg Fouriera dla funkcji argumentów rzeczywistych o wartościach rzeczywistych i użył funkcji sinus i cosinus w dekompozycji. Od tego czasu zdefiniowano wiele innych transformacji, rozszerzając jego początkowy pomysł na wiele zastosowań i tworząc dział matematyki zwany analizą Fourierowską.
Metoda Fouriera doprowadziła do przewrotu w matematyce i zainicjowała powstanie wielu nowych teorii. Dziś szeregi Fouriera mają wielkie znaczenie między innymi w fizyce, teorii drgań oraz przetwarzaniu sygnałów obrazu (kompresja jpeg) i dźwięku (kompresja mp3)[3].
Definicja za pomocą funkcji sin i cos[1]
Niech dana będzie funkcja okresowa o okresie bezwzględnie całkowalna w przedziale . Trygonometrycznym szeregiem Fouriera funkcji nazywamy szereg funkcyjny postaci
(1.1) |
o współczynnikach określonych wzorami:
(1.2) |
(1.3) |
Powyższe wzory po raz pierwszy opublikował Jeana-Baptiste Joseph Fourier. Niemniej jednak po raz pierwszy wyprowadził je Leonhard Euler (prac na ten temat nie opublikował). Wzory te noszą nazwę wzorów Eulera-Fouriera[4].
Wprowadzając dla uproszczenia oznaczenie w powyższych wzorach, gdzie to tzw. pulsacja lub częstość kołowa, otrzymamy:
(1.1a) |
(1.2a) |
(1.3a) |
Definicja za pomocą funkcji zespolonych[5]
Niech dana będzie funkcja okresowa o okresie bezwzględnie całkowalna w przedziale . Zespolonym szeregiem Fouriera funkcji nazywamy szereg funkcyjny
gdzie
Związek między współczynnikami rozwinięcia trygonometrycznego i zespolonego


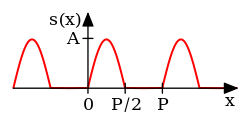
Rozważmy funkcję piłokształtną:
Obliczając jej współczynniki szeregu Fouriera otrzymamy:
i ostatecznie
Można pokazać, że szereg Fouriera zbiega do funkcji we wszystkich punktach , w których funkcja jest ciągła, tj.

Dla (i ogólnie dla ) szereg Fouriera zbiega do wartości 0. Wartość ta jest równa połowie sumy wartości granic lewo- i prawostronnych funkcji w punkcie . W punkcie funkcja nie została zdefiniowana. Jeżeli więc chcielibyśmy, by szereg był zbieżny do funkcji w tym punkcie (i ogólnie dla ), to należałoby uzupełnić jej definicję przyjmując:
Wniosek ten jest zawarty w twierdzeniu Dirichleta, które orzeka, iż[5]
Jeżeli funkcja jest w przedziale ograniczona i ciągła lub posiada nieciągłości najwyższej 1-go rodzaju (tj. spełniające warunek: w punkcie nieciągłości istnieją granice funkcji lewo- i prawostronna) i w skończonej liczbie, to (1) szereg Fouriera zbiega do funkcji w punktach ciągłości (2) w punktach nieciągłości szereg zbiega do wartości równej połowie sumy granic lewo- i prawostronnej funkcji w tych punktach.
Uwaga 1: Z powyższego przykładu widać, że funkcja rozwijana w szereg Fouriera może nie być zdefiniowana w punktach nieciągłości 1-go rodzaju - brak wartości funkcji w tych punktach nie przeszkadza w obliczaniu współczynników Fouriera ani nie ma wpływu na ich wartość (bowiem wartości całek nie zależą od wartości funkcji na zbiorze miary zero, a takiej miary jest zbiór punktów nieciągłości funkcji).
Uwaga 2: Powyższy przykład prowadzi do rozwiązania tzw. problemu bazylejskiego.

Funkcję nieokresową , określoną dla można rozwinąć w szereg Fouriera, obliczając współczynnika Fouriera jak dla funkcji okresowej o okresie . Szereg Fouriera jest zawsze funkcją okresową, nawet jeśli oryginalna funkcja nią nie jest. Jednak ograniczając się do wartości szeregu dla otrzymamy rozkład oryginalnej funkcji na szereg Fouriera.
Funkcja musi przy tym spełniać na przedziale zmienności te same warunki ograniczoności i ciągłości, co funkcja okresowa na przedziale .
Uwaga:
Jeżeli funkcja jest okresowa, to rozwinięcia w szereg Fouriera można dokonać na dowolnym przedziale , gdzie - dowolne przesunięcie powyższego zakresu; np. dla . Wtedy wystarczy obliczać całki na współczynniki rozwinięcia w innym zakresie.[1] Analogicznie dotyczy to rozwinięć funkcji nieokresowych na innych przedziałach zmienności zmiennej
Twierdzenie nt. dokładności aproksymacji
Tw. Przy zastąpieniu funkcji przybliżoną sumą trygonometryczną
średni błąd kwadratowy
jest najmniejszy, jeżeli za współczynniki przyjmie się współczynniki Fouriera funkcji [5].
Przykład

Powyższe twierdzenie orzeka, iż spośród wszystkich funkcji, przybliżających daną funkcję za pomocą skończonej kombinacji liniowej funkcji sinusoidalnych i kosinusoidalnych najmniejszy średni błąd kwadratowy uzyska się dla współczynników będących współczynnikami rozwinięcia danej funkcji w szereg Fouriera. Dla ilustracji pokazano tu przybliżenia funkcji (opisującej kat odchylania wahadła matematycznego od pionu) za pomocą dwóch funkcji o identycznych składowych harmonicznych, ale o różnych współczynnikach
(a) przybliżenie sumą częściową szeregu Fouriera funkcji
- ,
(b) przybliżenie funkcją , która jest rozwiązaniem przybliżenia równania nieliniowego ruchu wahadła za pomocą rozwinięcia w szereg Maclaurina członu nieliniowego tego równania:
gdzie:
- - amplituda drgań wahadła,
- , gdzie - okres drgań wahadła, słuszny dla dowolnych amplitud,
- - całka eliptyczna zupełna pierwszego rodzaju
Z obliczeń średniego błędu kwadratowego otrzymano:
(a) dla :
(a) dla :
Zwiększenie liczby wyrazów w liczeniu sumy częściowej Fouriera zmniejsza średni błąd kwadratowy; dla otrzymuje się . Widać stąd, iż analiza Fouriera stanowi skuteczne narzędzie znajdowania znakomitych aproksymacji rozwiązań równań różniczkowych.
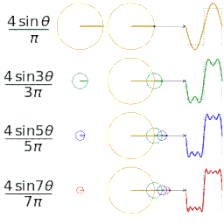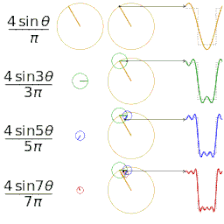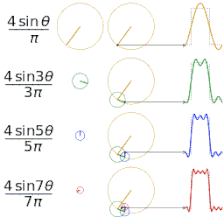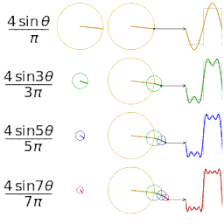
- Cztery sumy częściowe szeregu Fouriera zawierające 1, 2, 3 i 4 wyrazy, pokazujące, jak poprawia się przybliżenie funkcji prostokątnej ze wzrostem liczby wyrazów (tu dokładna animacja)
- Cztery sumy częściowe szeregu Fouriera zawierające 1, 2, 3 i 4 wyrazy, pokazujące, jak poprawia się przybliżenie funkcji piłokształtnej ze wzrostem liczby wyrazów (tu dokładna animacja)

Zależność aproksymacji od liczby wyrazów sumy aproksymującej
Dokładność aproksymacji danej funkcji za pomocą szeregu Fouriera zależy od liczby wyrazów N szeregu - im więcej wyrazów sumy częściowej, tym mniejszy jest średni błąd kwadratowy. Pokazują to poniższe animacje.
Efekt Gibbsa
Dla funkcji nieciągłych pojawia się tzw. efekt Gibbsa w aproksymacji - w punktach nieciągłości (odcinki skoków pionowych) następują silne odchylenia funkcji aproksymującej od wartości średniej, pomimo że maleje średni błąd kwadratowy aproksymacji danej funkcji za pomocą sum częściowych szeregu Fouriera wraz ze wzrostem liczby wyrazów sumy aproksymującej. W związku z tym stosuje się różne techniki wygładzania lokalnego funkcji aproksymującej w pobliży punktów nieciągłości.

Współczynniki szeregu Fouriera reprezentują amplitudy składowych harmonicznych , jakie zawiera dany sygnał. Zbiór tych współczynników nazywa się widmem danej funkcji.
Animacja obok pokazuje widmo funkcji, która ma jedynie składowe sinusoidalne widma.
Dalej pokazano widmo dla ogólnego przypadku.

Poniżej podano kod programu w języku Python, który dla danej funkcji liczy współczynniki szeregu Fouriera , oblicza funkcję aproksymującą funkcję wyjściową, rysuje funkcję daną i aproksymującą oraz rysuje widmo składowych harmonicznych, którego wartości są równe wartościom składowych szeregu Fouriera.
Użytkownik może ustalić:
- Parametr określający zakres , na którym jest zdefiniowana funkcja, taki że (linia 9 kodu)
- Liczbę wyrazów funkcji aproksymującej (linia nr 10)
- Definicję funkcji (linia nr 14)
- Program można testować, korzystając np. z darmowego notatnika colab google online.
# JK 2024.08.16 v.1 Program oblicza współczynniki szeregu Fouriera danej funkcji,
# rysuje wykres funkcji i funkcji aproksymujacej, rysuje wykres widma
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
# Parametry
L = np.pi # Okres (od -L do L)
N = 10 # Liczba wyrazów w szeregu Fouriera
# Definicja funkcji f(x) = x
def f(x):
return x*x-0.5*x**3
# Współczynniki a_n i b_n
a0 = (1 / L) * quad(f, -L, L)[0]
def a_n(n):
integrand = lambda x: f(x) * np.cos(n * np.pi * x / L)
result, _ = quad(integrand, -L, L)
return result / L
def b_n(n):
integrand = lambda x: f(x) * np.sin(n * np.pi * x / L)
result, _ = quad(integrand, -L, L)
return result / L
# Funkcja rekonstrukcji z szeregu Fouriera
def fourier_series(x, N):
a0_term = a0 / 2
sum_terms = sum(a_n(n) * np.cos(n * np.pi * x / L) + b_n(n) * np.sin(n * np.pi * x / L) for n in range(1, N + 1))
return a0_term + sum_terms
# Zakres x dla wykresu
x_values = np.linspace(-L, L, 500)
f_values = f(x_values)
fs_values = [fourier_series(x, N) for x in x_values]
# Obliczanie współczynników dla widma
n_values = np.arange(1, N + 1)
a_n_values = np.array([a_n(n) for n in n_values])
b_n_values = np.array([b_n(n) for n in n_values])
# Wykres funkcji i szeregu Fouriera
plt.figure(figsize=(14, 6))
# Wykres funkcji i szeregu Fouriera
plt.subplot(1, 2, 1)
plt.plot(x_values, f_values, label="f(x) = x*x-0.5*x**3", color="blue")
plt.plot(x_values, fs_values, label=f"Szereg Fouriera, N = {N}", color="red", linestyle="--")
plt.title("Funkcja f(x) i jej szereg Fouriera")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
# Wykres widma Fouriera
plt.subplot(1, 2, 2)
plt.stem(n_values, np.abs(a_n_values), linefmt='b-', markerfmt='bo', basefmt='b-', label='a_n')
plt.stem(n_values, np.abs(b_n_values), linefmt='r-', markerfmt='ro', basefmt='r-', label='b_n')
plt.title("Widmo Fouriera")
plt.xlabel("n")
plt.ylabel("Amplituda")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()



Podane tu dwa zasadnicze twierdzenia dotyczą warunków rozwinięcia za pomocą szeregu Fouriera funkcji okresowej. Zakładamy, że funkcja ma okres i pulsację Twierdzenia poprzedzone są lematami, potrzebnymi do ich dowodów.
Lemat I (całki pomocnicze)
- jest liczbą całkowitą
- są liczbami naturalnymi
Lemat II
Dowód
więc mamy (biorąc cześć rzeczywistą i stosując podstawowe wzory trygonometryczne):
q. e. d.
Lemat III
Jeżeli jest funkcją ciągłą w przedziale z wyjątkiem co najwyżej skończonej ilości punktów i bezwzględnie całkowalną w tym przedziale to
Twierdzenie (Eulera–Fouriera)
Jeżeli szereg o postaci (1.1) jest jednostajnie zbieżny do funkcji to współczynniki wyrażają się wzorami (1.2), (1.3).
Dowód
Mnożąc powyższą równość przez całkując szereg w granicach od do (uwzględniając zbieżność jednostajną szeregu stosujemy twierdzenie o całkowaniu szeregu wyraz po wyrazie) otrzymujemy:
Na mocy lematu I zerują się wszystkie całki po prawej stronie takie że (gdy zeruje się cała suma uogólniona). W związku z tym mamy:
Stąd otrzymujemy wzór (1.2).
Dowód wzoru (1.3) przebiega analogicznie (tym razem mnożymy przez )
Twierdzenie (o rozwijalności funkcji w szereg Fouriera)
Jeżeli funkcja jest różniczkowalna w punkcie to jej szereg Fouriera jest zbieżny do wartości funkcji w tym punkcie.
Innymi słowy: W punktach różniczkowalności funkcję da się rozwinąć w szereg Fouriera.
Dowód
Niech będzie punktem, w którym funkcja jest różniczkowalna; mamy:
Suma cząstkowa szeregu Fouriera przedstawia się w następujący sposób:
Stosując do tego wyrażenia lemat II, otrzymujemy następujący wzór:
Funkcja podcałkowa w powyższym wzorze jest funkcją o okresie T, możemy więc dokonać przesunięcia w dziedzinie i otrzymujemy:
Funkcja tożsamościowo równa 1 na całym zbiorze liczb rzeczywistych jest rozwijalna w szereg Fouriera w każdym punkcie, kładąc mamy:
Mnożąc powyższą równość przez i odejmując obustronnie od równania przedstawiającego sumę cząstkową szeregu, otrzymujemy:
(2) |
Rozważmy następującą granicę:
przy obliczaniu której korzystamy z różniczkowalności funkcji f(x) w punkcie
Możemy określić następującą funkcję:
Mając na uwadze fakt, iż zmiana skończonej ilości wartości funkcji podcałkowej nie wpływa na wartość całki, wzór (2) możemy zapisać w postaci:
Funkcja podcałkowa spełnia założenia lematu Riemanna, tak więc:
czyli:
q. e. d.
Baza zespolona szeregu Fouriera
Uwaga: W poniższych rozważaniach przyjęto, iż szereg Fouriera jest funkcją o okresie . W przypadku wszystkie własności pozostają nadal prawdziwe, gdyż wystarczy przeskalować daną funkcję do funkcji o okresie .
Zbiór funkcji tworzy bazę ortonormalną przestrzeni funkcji całkowalnych w kwadracie na przedziale , w której iloczyn skalarny dwóch jej elementów oraz ma postać całkową:
gdzie oznacza sprzężenie zespolone funkcji gdyż
Przestrzeń funkcyjna z tak zdefiniowanym iloczynem skalarnym jest nazywana przestrzenią Hilberta. Każdą funkcję tej przestrzeni można rozłożyć w jej bazie ortonormalnej w postaci szeregu
Powyższy szereg przedstawia de facto szereg Fouriera funkcji w jego zespolonym sformułowaniu, gdzie zamiast funkcji bazowych oraz mamy funkcje zespolone .
Baza ortogonalna z funkcji sin i cos szeregu Fouriera

Jako bazę ortogonalną w przestrzeni funkcji całkowalnych w kwadracie na przedziale można także wybrać funkcję stałą oraz funkcje , dla Analogicznie więc, jak dla bazy zespolonej, także szereg Fouriera z funkcjami sinus oraz cosinus przedstawia rozkład danej funkcji w bazie przestrzeni Hilberta.
Ortogonalność funkcji oraz wraz z funkcją stałą wynika z poniższych całek:
gdzie gdy , gdy (tj. oznacza symbol Kroneckera)
W tabeli zestawiono popularne funkcje okresowe i ich współczynniki szeregu Fouriera
- oznacza funkcję okresową o okresie
- oznaczają współczynniki szeregu Fouriera w formie trygonometrycznej (sin-cos) dla funkcji okresowych .
Tabela zestawia operacje matematyczne wykonywane na danych funkcjach i wpływ tych operacji na współczynniki szeregów Fouriera oraz wpływ operacji wykonywanych na współczynnikach Fouriera i ich wpływ na dane funkcje. Notacja:
- Sprzężenie zespolone jest oznaczane gwiazdką.
- oznaczają -okresowe funkcje lub funkcje nieokresowe, zdefiniowane tylko dla
- oznaczają współczynniki szeregów Fouriera w postaci zespolonej odpowiednio dla funkcji oraz
| Własności | Dziedzina funkcji | Dziedzina częstotliwości (dla postaci zespolonej szeregu) | Uwagi |
|---|---|---|---|
| Liniowość | |||
| Odwrócenie czasu / Odwrócenie częstotliwości | |||
| Sprzężenie w dziedzinie czasu | |||
| Odwrócenie w dziedzinie czasu i sprzężenie | |||
| Obliczanie części rzeczywistej funkcji | |||
| Obliczanie części urojonej funkcji | |||
| Obliczanie części rzeczywistej współczynnika częstotliwości | |||
| Obliczanie części urojonej współczynnika częstotliwości | |||
| Przesunięcie w czasie w danej funkcji / modulacja współczynników częstotliwości | |||
| Przesunięcie współczynników częstotliwości / modulacja danej funkcji |
Szereg Fouriera dla funkcji dwóch zmiennych oraz określonych w dziedzinie w formie zespolonej ma postać:
gdzie współczynniki rozwinięcia dane są wzorem
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.


![{\displaystyle \left[{\tfrac {-T}{2}},{\tfrac {T}{2}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b3cbbb28fa89cba2e6376fd1d6a98d7f61f4121e)

![{\displaystyle S(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left({\frac {2\pi }{T}}\,nx\right)+b_{n}\sin \left({\frac {2\pi }{T}}\,nx\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ce0c188a5b7804f21a68f6e16950855a480c92ef)




![{\displaystyle S(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(n\omega x\right)+b_{n}\sin \left(n\omega x\right)\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/07e14695cc8dc06888eaf30aac436b4c99446fb5)



![{\displaystyle \left[-{\tfrac {T}{2}},{\tfrac {T}{2}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ac4e11b9d1ed4eaf84913b83dcaf0ba521d2c5d0)













![{\displaystyle {\begin{aligned}S(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {dla} \ x\neq \pm \pi ,\pm 3\pi ,\pm 5\pi ,\dots \end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2a8dddfba3749e5595cfee35e5c97c96a8b7e9b6)





![{\displaystyle [0,L]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/53e3bfad6c2b8297e8c8d2e84ce8f869d69b0d86)

![{\displaystyle x\in [-{\tfrac {L}{2}},{\tfrac {L}{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a1757f5106407e1a5b7cc971815eb6471e543b49)


![{\displaystyle x\in [-{\tfrac {L}{2}}+x_{0},{\tfrac {L}{2}}+x_{0}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/77e7c6975ce9eb72f59c4827612d3504aa5b7b04)

![{\displaystyle x\in [0,L]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d35e3fa30fa9d0e9f57923fb0101848d4fea625a)

![{\displaystyle S_{N}(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\,[a_{n}\cos(nx)+b_{n}\sin(nx)]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5e335153c3998f25f0c838791debc794ed3b1fbd)
![{\displaystyle \delta ^{2}={\frac {1}{T}}\int \limits _{-T/2}^{T/2}[f(x)-S_{N}(x)]^{2}dx}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bb7e2275800ccb40932c51450ba2a9a57bf3f8d7)


























![{\displaystyle [-L,L]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3821e4ce807a6a5d059c66d3c8802a17a8d6e92c)













![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






























![{\displaystyle L^{2}([-\pi ,\pi ])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)
![{\displaystyle [-\pi ,\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)































 ...
...









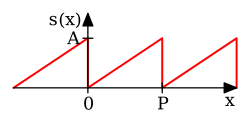








![{\displaystyle x\in [0,T].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d2a28f37ee6639c429c6470c1fc35bd967b75b80)
![{\displaystyle S[n],R[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)

 ,
,  ...
...

![{\displaystyle S[-n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i2\pi {\tfrac {x_{0}}{P}}n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7c56731e1382c8189ca81104cbade4d310fd72d8)


![{\displaystyle S[n-n_{0}]\!}](http://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)


![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)

