Metrisk tensor

En metrisk tensor benyttes i differensialgeometrien til å definere indreproduktet mellom to vektorer på en flate eller mer generell mangfoldighet. Den gir derfor lengden og vinkelen mellom to vektorer i samme punkt. Den er en symmetrisk tensor av rang to som inneholder all informasjon om avstanden mellom alle par av nærliggende punkt. Ved integrasjon kan den derfor gi avstanden mellom to vilkårlige punkt og gjør det derfor mulig å beregne geodetiske kurver på mangfoldigheten. Tensoren opptrer også ved bruk av krumlinjete koordinater i euklidske rom. I Einsteins generelle relativitetsteori inneholder den all informasjon om de geometriske egenskapene til tidrommet og er en relativistisk generalisering av Newtons gravitasjonspotensial.

En bedre forståelse av den metriske tensorens betydning kom med etableringen av riemannsk geometri som fikk sitt navn etter Bernhard Riemann. Men den var tidligere implisitt benyttet av Carl Friedrich Gauss i hans utarbeidelse av differensiell flategeometri. På samme måte opptrer den også i arbeidene til Nikolaj Lobatsjevskij om ikke-euklidsk geometrier.

Mindre presist blir den metriske tensoren i mange sammenhenger ganske enkelt omtalt som «metrikken».

Euklidsk rom

I et 3-dimensjonalt, euklidsk rom kan man benytte et kartesisk koordinatsystem med basisvektor e_x, e_y og e_z  kan enhver vektor v uttrykkes ved sine komponenter som v = v_x e_x + v_y e_y + v_z e_z. Basisvektorene står vinkelrett på hverandre som betyr at deres indreprodukt er gitt ved Kronecker-symbolet som

${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=\delta _{ij}}$

Det er null når indeksene er forskjellige og lik med en når de er de samme. Bruker man Einsteins summekonvensjon hvor man summerer over alle par av like indekser, kan en vektor da skrives som v = v_k e_k. Den kvadrerte lengden av vektoren

${\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}$

kan da skrives mer kompakt som

${\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{i}\mathbf {e} _{i}\cdot v_{j}\mathbf {e} _{j}=\delta _{ij}v_{i}v_{j}}$

På samme måte blir indreproduktet med en annen vektor u = u_k e_k

${\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{i}\mathbf {e} _{i}\cdot v_{j}\mathbf {e} _{j}=\delta _{ij}u_{i}v_{j}}$

Disse uttrykkene ville være de samme hvis dette rommet hadde et annet antall dimensjoner som bestemmer hvor mange komponenter vektorene har og derfor hvor mange ledd som inngår i summasjonene.

Skjevvinklet koordinatsystem

I det euklidske rommet kan man benytte andre koordinatsystem enn det kartesiske. Bruker man i stedet skjevvinklete koordinater, vil basisvektorene ikke lenger stå vinkelrett på hverandre. Skriver man disse nye vektorene med greske indekser, vil de derfor være lineærkombinasjoner av de kartesiske basisvektorene med latinske indekser. Dette kan sammenfattes i uttrykket

${\displaystyle \mathbf {e} _{\mu }=\mathbf {e} _{m}M_{\;\;\mu }^{m}}$

hvor igjen summekonvensjonen benyttes. Her kan konstantene M^m_μ  betraktes som m-te komponent av den nye basisvektoren e_μ. De kan alle grupperes i en matrise som kalles «transformasjonsmatrisen». Denne har en invers M^-1  når den nye basisen er lineært uavhengig og derfor utspenner hele rommet. Man kan da uttrykke de kartesiske basisvektorene ved de nye,

${\displaystyle \mathbf {e} _{m}=\mathbf {e} _{\mu }(M^{-1})_{\;\;m}^{\mu }}$

En generell vektor v  får i dette koordinatsystemet nye komponenter. Den kan skrives som v = v^μ e_μ  da det vil vise seg å være hensiktsmessig og skrive den greske indeksen til vektorkomponenten på «hevet» eller «øvre» plass. Latinske indekser kan stå opp eller nede uten at det gjør noen forskjell. Dermed har man at

${\displaystyle \mathbf {v} =v^{m}\mathbf {e} _{m}=v^{m}\mathbf {e} _{\mu }(M^{-1})_{\;\;m}^{\mu }}$

De nye vektorkomponentene er derfor

${\displaystyle v^{\mu }=(M^{-1})_{\;\;m}^{\mu }v^{m}}$

Mens den nye basisen transformerer med matrisen M, transformerer komponentene ved den inverse matrisen.

Indreproduktet av to vektorer u og v i dette skjevvinklete koordinatsystemet blir nå

${\displaystyle \mathbf {u} \cdot \mathbf {v} =u^{\mu }\mathbf {e} _{\mu }\cdot v^{\nu }\mathbf {e} _{\nu }\equiv g_{\mu \nu }u^{\mu }v^{\nu }}$

hvor nå

${\displaystyle g_{\mu \nu }=\mathbf {e} _{\mu }\cdot \mathbf {e} _{\nu }}$

utgjør komponentene til det som kalles den metriske tensoren. Den er symmetrisk i den forstand at g_μν = g_νμ. Det tilsvarende produktet v⋅v = |v|²  gir også lengden |v|  av hver vektor uttrykt ved komponentene v^μ. På samme måte kan man finne vinkelen θ  mellom to vektorer når deres komponenter er kjente,

${\displaystyle \cos \theta ={\mathbf {u} \cdot \mathbf {v} \over |\mathbf {u} ||\mathbf {v} |}}$

Den metriske tensoren gjør det derfor mulig å regne med vektorer i det skjevvinklete koordinatsystemet i stor grad på samme måte som i det euklidske rommet. For praktiske fremstillinger samles ofte komponentene g_μν  i en N×N matrise hvor N  er dimensjonen til rommet under betraktning.

Setter man inn uttrykket for de transformerte basisvektoren i definisjonen av g_μν, blir

${\displaystyle g_{\mu \nu }=\mathbf {e} _{m}M_{\;\;\mu }^{m}\mathbf {e} _{m}\cdot \mathbf {e} _{n}M_{\;\;\nu }^{n}\mathbf {e} _{n}=M_{\;\;\mu }^{m}M_{\;\;\nu }^{n}\delta _{mn}}$

Mens vektorer transformer ved en M-matrise, tranformerer disse komponentene ved to slike matriser. De utgjør derfor tilsammen en tensor av andre rang. Transformasjonsmatrisen M  gir sammenhengen mellom komponentene til denne tensoren i det skjeve koordinatsystemet med komponentene i det kartesiske systemet. I dette opprinnelige koordinatsystemet kan man derfor si at den metriske tensoren ikke er noe annet enn Kronecker-deltaet δ_mn. Metrikken til det euklidske rommet i et kartesisk koordinatsystem er derfor gitt ved identitetsmatrisen.

Kovariante og kontravariante komponenter

Mens basisvektorene e_μ  transformerer ifølge matrisen M, vil komponentene v^μ  transformere ifølge den inverse matrisen M^-1. Disse komponentene kalles derfor for «kontravariante». Fra definisjonen v = v^μ e_μ  ser man at de geometrisk finnes ved å projisere vektoren parallelt langs de forskjellige koordinataksene. Man kan alternativt foreta projeksjonen normalt på de samme aksene, noe som i så fall gir de «kovariante» komponentene. De skrives som v_μ  og transformerer på samme måte som basisvektorene.

Matematisk etableres dette ved å innføre nye basisvektorer e^μ  som står normalt på de tidligere. Dette kalles en «dual basis» som skal oppfylle

${\displaystyle \mathbf {e} ^{\mu }\cdot \mathbf {e} _{\nu }=\delta _{\,\nu }^{\mu }}$

Disse nye basisvektorene vil derfor transformeres ved den inverse matrisen M^-1, mens de tilsvarende komponentene i dekomposisjonen v = v_μ e^μ  transformeres ved M og er derfor kovariante.

Forbindelsen mellom disse to settene med kovariante og kontravariante komponenter er den metriske tensoren. For eksempel, da

${\displaystyle v_{\mu }=\mathbf {e} _{\mu }\cdot \mathbf {v} =\mathbf {e} _{\mu }\cdot v^{\nu }\mathbf {e} _{\nu }=g_{\mu \nu }v^{\nu }}$

sier man at metrikken kan senke en kontravariant indeks. På tilsvarende måte kan en kovariant indeks heves da

${\displaystyle v^{\mu }=\mathbf {e} ^{\mu }\cdot \mathbf {v} =\mathbf {e} ^{\mu }\cdot v_{\nu }\mathbf {e} ^{\nu }=g^{\mu \nu }v_{\nu }}$

etter å ha definert

${\displaystyle g^{\mu \nu }=\mathbf {e} ^{\mu }\cdot \mathbf {e} ^{\nu }}$

Det betyr at

${\displaystyle g^{\mu \nu }g_{\nu \lambda }=\delta _{\,\lambda }^{\mu }}$

slik at de kontravariante komponentene g^μν  utgjør en matrise som er den inverse av matrisen med komponentene g_μν. På samme måte kan indekser til en generell tensor heves og senkes.

Med disse komponentene kan den metriske tensoren skrives på de ekvivalente måtene

${\displaystyle \mathbf {g} =g_{\mu \nu }\mathbf {e} ^{\mu }\otimes \mathbf {e} ^{\nu }=g^{\mu \nu }\mathbf {e} _{\mu }\otimes \mathbf {e} _{\nu }=\delta _{\,\nu }^{\mu }\mathbf {e} _{\mu }\otimes \mathbf {e} ^{\nu }=\mathbf {e} _{\mu }\otimes \mathbf {e} ^{\mu }}$

Den kan derfor betraktes som en enhetstensor. Ved praktiske beregninger må de eksplisitte komponentene benyttes.

Eksempel

Kovariante og kontravariante komponenter av en vektor fremkommer ved projeksjoner vinkelrett og parallelt på skjeve koordinatakser.

I to dimensjoner kan man benytte et skjevvinklet koordinatsystem med basisvektorene e₁ = e_x  og e₂ = cosθ e_x + sinθ e_y  hvor θ er en vilkårlig vinkel. Herav finner man direkte fra definisjonen komponentene til den metriske tensoren

${\displaystyle g_{\mu \nu }={\begin{bmatrix}g_{11}&g_{21}\\g_{21}&g_{22}\end{bmatrix}}={\begin{bmatrix}1&\cos \theta \\\cos \theta &1\end{bmatrix}}}$

Herav finnes de kontravariante komponentene fra den inverse matrisen som er

${\displaystyle g^{\mu \nu }={\begin{bmatrix}g^{11}&g^{21}\\g^{21}&g^{22}\end{bmatrix}}={1 \over \sin ^{2}\theta }{\begin{bmatrix}1&-\cos \theta \\-\cos \theta &1\end{bmatrix}}}$

Har man en vektor A = cosα e_x + sinα e_y med lengde lik en, har den nå de kovariante komponentene A₁ = e₁⋅A = cosα  og A₂ = e₂⋅A = cos(θ - α). De fremkommer ved å projisere vektoren normalt på de to basisvektorene.

De kontravariante komponentene kan beregnes ved hjelp av metrikken. De blir

${\displaystyle A^{1}=g^{1\mu }A_{\mu }=g^{11}A_{1}+g^{12}A_{2}={1 \over \sin ^{2}\theta }{\Big (}1\cdot \cos \alpha -\cos \theta \cdot \cos(\theta -\alpha ){\Big )}=\cos \alpha -\cot \theta \sin \alpha }$

${\displaystyle A^{2}=g^{2\mu }A_{\mu }=g^{21}A_{1}+g^{22}A_{2}={1 \over \sin ^{2}\theta }{\Big (}-\cos \theta \cdot \cos \alpha +1\cdot \cos(\theta -\alpha ){\Big )}={\sin \alpha \over \sin \theta }}$

Resultatet viser seg som ventet å være komponentene projisert parallelt inn på basisvektorene.

Riemannske rom

Hvis man i et N-dimensjonalt, euklidsk rom benytter kartesiske koordinater, vil hvert punkt i rommet kunne angis ved posisjonsvektoren r = x^me_m. En flate i dette rommet ville beskrives ved å la disse koordinatene ble funksjoner av to nye variable slik at x^m = x^m(u,v) hvor u og v kan tas som koordinatene på denne flaten. På samme måte, hvis de kartesiske koordinatene blir funksjoner av N' < N nye variable x^μ, vil de beskrive et N' -dimensjonalt, riemannsk rom som ligger i det euklidske rommet. Derimot hvis N' = N, vil de variable x^μ være krumlinjete koordinater i dette euklidske rommet.

I det riemannske rommet er hvert punkt gitt ved koordinattransformasjonene x^m = x^m(x^μ). Ved å variere kun en av koordinatene x^μ  og holde de andre konstant, beskriver disse ligningene en tilsvarende «koordinatlinje» i rommet. Gjennom hvert punkt går det N'  slike linjer som generelt vil være krummet. Det gjør det mulig i hvert punkt å innføre lokale basisvektorer e_μ  som er tangentvektorer til koordinatlinjene,

${\displaystyle \mathbf {e} _{\mu }={\partial \mathbf {r} \over \partial x^{\mu }}={\partial x^{m} \over \partial x^{\mu }}\mathbf {e} _{m}}$

Denne basisvektorene vil i alminnelighet variere fra punkt til punkt. To punkt i det riemannske rommet som adskiller seg med de infinitesemale koordinatdifferansene dx^μ, vil være separert ved den infinitesemale, euklidske vektoren d r = dx^μ e_μ. Den differensielle avstanden mellom de to nærliggende punktene er derfor gitt ved det kvadrerte linjeelementet eller buelengden ds² = d r⋅d r = e_μ⋅e_νdx^μdx^ν. Vanligvis skrives dette som

${\displaystyle ds^{2}=g_{\mu \nu }dx^{\mu }dx^{\nu }}$

hvor g_μν = e_μ⋅e_ν er komponentene til den metriske tensoren i det riemannske rommet. I alminnelighet vil disse også variere fra punkt til punkt i motsetning til metrikken i et skjevvinklet koordinatsystem. Ved å angi linjeelementet i et riemannsk rom, vil man da også automatisk kjenne til alle komponentene til den metriske tensoren som er forskjellig fra null. Ofte er dette den enkleste måten å angi de metriske egenskapene til rommet.

Enhver vektor v kan i denne basisen nå skrives som v = v^μ e_μ  uttrykt ved sine kontravariante komponenter v^μ. De kovariante komponentene kan igjen beregnes ved hjelp av metrikken som v_μ = g_μνv^ν. Den motsatte sammenhengen kan igjen finnes fra de kontravriante komponentene g^μν til metrikken. Igjen finnes de ved å konstruere den inverse av matrisen (g_μν). Geometrisk fremkommer disse komponentene som projeksjoner på en «dual» basis. De kan konstrueres ved at man i en begrenset del av rommet inverterer koordinattransformasjonen slik at den tar formen x^μ = x^μ(x^m). Normalvektorene e^μ = ∇x^μ  til koordinatflatene x^μ = konstant utgjør da det duale settet med basisvektorer. De vil tilfredsstille relasjonene

${\displaystyle \mathbf {e} ^{\mu }\cdot \mathbf {e} _{\nu }={\boldsymbol {\nabla }}\!x^{\mu }\cdot {\partial \mathbf {r} \over \partial x^{\nu }}={\partial x^{\mu } \over \partial x^{\nu }}=\delta _{\;\nu }^{\mu }}$

som betyr at den metriske tensoren kan brukes i det krumme, riemannske rommet på samme måte som i et flatt, euklidsk rom.

Eksempel

Sfærisk koordinatsystem. Basisvektorene er tangentvektorer til koordinatlinjene.

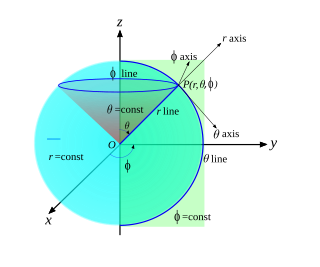
I et tredimensjonalt, euklidsk rom kan man benytte kulekoordinater (r, θ, φ). som også ofte omtales som sfæriske koordinater. Sammenhengen med de kartesiske koordinatene er da gitt ved transformasjonsligningene

${\displaystyle x=r\sin \theta \,\cos \varphi }$

${\displaystyle y=r\sin \theta \,\sin \varphi }$

${\displaystyle z=r\cos \theta }$

Fra disse kan man så direkte finne de nye basisvektorene

${\displaystyle {\begin{aligned}\mathbf {e} _{r}&=\sin \theta \cos \varphi \,\mathbf {e} _{x}+\sin \theta \sin \varphi \,\mathbf {e} _{y}+\cos \theta \,\mathbf {e} _{z}\\\mathbf {e} _{\theta }&=r\cos \theta \,\cos \varphi \,\mathbf {e} _{x}+r\cos \theta \,\sin \,\varphi \,\mathbf {e} _{y}-r\sin \theta \,\mathbf {e} _{z}\\\mathbf {e} _{\varphi }&=-r\sin \theta \sin \varphi \,\mathbf {e} _{x}+r\sin \theta \cos \,\varphi \,\mathbf {e} _{y}\\\end{aligned}}}$

Ved å ta indreprodukt mellom disse finner man komponentene til den metriske tensoren i dette koordinatsystemet som

${\displaystyle g_{\mu \nu }={\begin{bmatrix}1&0&0\\0&r^{2}&0\\0&0&r^{2}\sin ^{2}\theta \end{bmatrix}}}$

Det tilsvarende linjeelementet i det tredimensjonale rommet er derfor

${\displaystyle ds^{2}=dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})}$

Denne metrikken beskriver fremdeles et euklidsk rom. Det kan man verifisere ved å regne ut Riemann-tensoren. Man finner da at alle komponentene er lik med null som viser at rommet er flatt.

Når radius r = a er konstant, vil transformasjonsligningene beskrive et todimensjonalt, riemannsk rom som er lagt inn i det tredimensjonale, euklidske rommet. Med andre ord, de beskriver en kuleflate med radius a og koordinater (θ, φ). Metrikken på denne flaten er da

${\displaystyle ds^{2}=a^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})}$

Denne er ikke lenger euklidsk. Regner man herav ut flatens krumning, finner man verdien K = 1/a². Den har derfor samme veri overalt, noe som viser at kuleflaten har spesielt stor symmetri.

Relativitetsteori

I et tilstrekkelig lite område på en kuleflate, vil man ikke merke at den er krummet. Den synes å være euklidsk. Dette gjelder for alle riemannske rom og er den grunnleggende idé som Riemann benyttet for å utvikle denne delen av moderne matematikk. Helt på tilsvarende vis fant Einstein frem til generell relativitetsteori ved å anta at i tilstrekkelige små områder av det firedimensjonale tidrommet vil den spesielle relativitetsteorien gjelde. Det er ekvivalensprinsippet. I den kovariante formuleringen er tidrommet et «pseudo-euklidsk» rom med koordinater (ct, x, y, z) og metrikken

${\displaystyle ds^{2}=\eta _{\mu \nu }dx^{\mu }dx^{\nu }=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}}$

hvor c  er lyshastigheten. Med disse koordinatene er derfor denne Minkowski-metrikken diagonal med komponentene η_μν = diag(1, -1, -1, -1). Dette er ikke et ekte, euklidsk rom da noen av komponentene er negative. Det kvadrerte linjeelementet kan derfor også ta negative verdier som er et uttrykk for kausalitet i tidrommet.

Man kan også her benytte andre koordinater. Hvis man for eksempel vil benytte kulekoordinater (r, θ, φ) for den romlige delen, kan metrikken skrives som

${\displaystyle ds^{2}=c^{2}dt^{2}-dr^{2}-r^{2}d\Omega ^{2}}$

når man i den angulære delen innfører ${\displaystyle d\Omega ^{2}=d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}}$. Matematisk kan man beskrive dette rommet på samme måte som alle andre riemannske rom. Man finner da at dette Minkowski-rommet er flatt da alle komponentene til Riemann-tensoren er null.

Generell relativitetsteori

I sin generelle relativitetsteori viste Einstein at det som vi opplever som tyngdekraft, skyldes at masse og energi vil forandre metrikken til tidrommet slik at det får en krumning. Generelt vil det da ikke lenger være beskrevet ved den konstante Minkowski-metrikken η_μν, men i stedet med en metrisk tensor g_μν  som varierer fra sted til sted. Kjenner man til fordeling av energi og masse gitt ved energi-impulstensoren, kan denne nye metrikken beregnes ut fra Einsteins gravitasjonsligning. Er gravitasjonspotensialet Φ  svakt, kan metrikken skrives som

${\displaystyle ds^{2}=c^{2}(1+2\Phi /c^{2})dt^{2}-(1-2\Phi /c^{2})(dx^{2}+dy^{2}+dz^{2})}$

De nye faktorene med gravitasjonspotensialet viser at tidrommet nå har en ikke-euklidsk geometri. Men denne modifiserte metrikken forklarer nå både rødforskyvning av lyset som blir sendt ut fra Solen og hvordan lysets bane forbi den blir avbøydd. Etter en mer komplisert beregning kunne også Einstein herav gi en løsning på det gamle problemet forbundet med bevegelsen av perihelium til planeten Merkur.

Sorte hull

Det finnes få eksakte løsninger av Einsteins gravitasjonsligning. Men en av de enkleste ble funnet av Karl Schwarzschild allerede i 1916, samme år som Einstein publiserte sin teori. Denne Schwarzschild-metrikken utenfor en sfærisk masse M kan skrives som

${\displaystyle ds^{2}=c^{2}\left(1-2GM/rc^{2}\right)dt^{2}-{dr^{2} \over 1-2GM/rc^{2}}-r^{2}d\Omega ^{2}\,}$

hvor G  er gravitasjonskonstanten. Selv om koordinaten r  gir omkretsen 2π r  for en sirkel sentrert i massen, kan den likevel ikke her identifiseres med en radiell avstand. Spesielt blir det klart for den spesielle verdien

${\displaystyle r_{S}={2GM \over c^{2}}}$

som er Schwarzschilds radius. Sammenligner man dette resultatet med uttrykket for metrikken i den svake grensen, ser man at når r blir veldig stor i forhold til r_S, vil metrikken beskrive tidrommet med et gravitasjonspotensial Φ = - GM/r  i overensstemmelse med Newtons gravitasjonslov.

Har massen M en utstrekning mindre enn Schwarzschild-radien, beskriver metrikken et sort hull med en «horisont» for r = r_S. Da vil de metriske komponentene g_tt  og g_rr  bytte fortegn. På samme måte som tiden t  alltid øker utenfor horisonten, vil koordinaten r  da alltid avta innenfor horisonten. Det betyr at all bevegelse innenfor denne fører inn i «singulariteten» for r = 0.

Litteratur

• G.E. Hay, Vector and Tensor Analysis, Dover Publications, New York (1953). ISBN 0-486-60109-9.
• M. R. Spiegel, Vector Analysis, Schaum's Outline Series, New York, (1959).
• C.W. Misner, K.S. Thorne and J.A. Wheeler, Gravitation, W. H. Freeman, San Francisco (1973). ISBN 0-7167-0344-0.

Eksterne lenker

• G. Berge, Vektor og tensoranalyse Arkivert 23. mars 2017 hos Wayback Machine., forelesninger ved Universitetet i Bergen (2004).