From Wikipedia, the free encyclopedia
Innen kryptografi er cæsarchiffer, også kjent som Caesars chiffer, skiftchiffer, Cæsars kode og cæsarskift, en av de enkleste og mest kjente krypteringsteknikker. Det er en type substitusjonschiffer der hver bokstav i klarteksten erstattes med en annen bokstav et gitt antall steg lenger ut i alfabetet. Med et skift på tre steg erstattes D med A, E med B, F med C og så videre. Metoden har navn etter Julius Cæsar som benyttet denne koden til å kommunisere med sine generaler.
Selv om cæsarchiffer er meget enkelt, så inngår det likevel ofte i mer komplekse krypteringsstrukturer som vigenèrechifferet. En finner det også igjen i moderne anvendelser som ROT13. Cæsarchiffer i seg selv, som et monoalfabetisk substiusjonschiffer, er i dag et meget enkelt system å bryte og gir ingen kommunikasjonssikkerhet. Det egner seg imidlertid til en første introduksjon til kryptering.
Transformasjonen kan lett gjennomføres ved å stille opp to alfabet: det ene representerer klarteksten, det andre er forskjøvet, eller rotert, og representerer chifferteksten. I eksempelet under er forskyvningen 3 plasser. Parameteren som angir antall skift, her 3, fungerer som nøkkel.
Klartekst: ABCDEFGHIJKLMNOPQRSTUVWXYZ Chiffertekst: DEFGHIJKLMNOPQRSTUVWXYZABC
Under chiffrering leter en opp den aktuelle klartekstbokstaven i øvre linje og erstatter den med bokstaven under. Ved dechiffrering går en motsatt fra nedre linje til den øvre.
Klartekst: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ Chiffertekst: the quick brown fox jumps over the lazy dog
Chiffreringen kan også gjøres ved å benytte modulær aritmetikk. Først erstattes alle bokstaver med tall etter følgende oppsett: A = 0, B = 1,..., Z = 25.[1]
Chiffrering av en klartekstbokstav med en forskyvning på tegn i et alfabet med 26 tegn er da gitt ved:[2]
Tilsvarende uttrykkes dechiffreringen av en hemmelig bokstav :
(Det er noe forskjellige definisjoner av modulooperasjonen. I eksempelet over har en antatt et alfabet med 26 karakterer, altså at svaret skal ligge i området 0...25. I.e., hvis x+n eller x-n ikke ligger i området 0...25, må en trekke fra eller legge til 26.)
Forskyvningen er her den samme gjennom hele meldingen. Dermed klassifiseres Cæsarchiffer som et enkelt substitusjonschiffer i motsetning til et polyalfabetisk chiffer.
.JPG)
Cæsarchiffer har navn etter den romerske keiser Julius Cæsar som, ifølge Suetonius, brukte det med et skift på tre steg for å beskytte militære meldinger. En kjenner også til at substitusjonschiffer også er anvendt enda tidligere.
Skulle han meddele noe konfidensielt så skrev han i kode, det vil si ved å endre rekkefølgen på bokstavene i alfabetet slik at intet ord kunne forstås. Hvis noen ønsker å dekode dette og få frem meningen, så må han erstatte den fjerde bokstaven i alfabetet, nemlig D med A og så videre for de resterende.
Hans nevø, Augustus, brukte også et slikt chiffer, men med en forskyvning på én:
Det er også indikasjoner på at Julius Cæsar også benytter mer kompliserte systemer.[3] En annen nedtegnelse fra Aulus Gellius viser til ??? and one writer, , refers to a (now lost) treatise on his ciphers:
Det ukjent om cæsarchiffer var en tilstrekkelig sikker for sin tid, men en kan anta at den var rimelig sikker. Dette fordi motstanderen både måtte være lesekyndig, kjenne latinsk språk og ikke forveksle koden med en melding skrevet i et annet fremmed språk.[4] En har ikke funnet noen beskrivelse fra den tid som angir noen teknikk for å løse selv et så enkelt chiffer som et monoalfabetisk substitusjonschiffer. Den første kjente nedtegnelsen etter Al-Kindi er fra det 9. århundre som omtaler arabernes oppdagelse av frekvensanalyse[5]
På baksiden av Mezuza er det vanlig å finne «כוזו במוכסז כוזו» som er et cæsarchiffer med et skift på én. Ordene er hentet fra Shemas 3. 4. og 5. ord: Adonai, Eloheinu, Adonai, «Herren, vår Gud, Herren». Dette kan være en reminisens fra tidlig tid da jødene da Mezuza var forbudt.[6]
Under personlig-spalten i fant en i det 19. århundre tidvis beskjeder som var kryptert med enkle krypteringsmetoder. Kahn beskriver forekomster der forelskede par har benyttet cæsarchiffer i The Times.[7] Endog så sent som i 1915 ble cæsarchiffer benyttet: Den russiske arme tok det i bruk i stedet for sikrere, men mer kompliserte metoder - metoder som viste seg å være for vanskelig for de russiske troppene å beherske. Tyske og australske kryptoanalytikere hadde dermed lite problemer med å dechiffrere de russiske meldingene.[8]
Cæsarchiffer kan en fortstatt finne i leketøy slik som i hemmelige dekoderringer. Cæsarchiffrering med et skift på tretten finnes i ROT13 algoritmen som en enkel måte å «skjule» informasjon i Usenet. En kan også finne det i form av tilsløring av poenget i en spøk eller for å gjøre det noe vanskeligere å avdekke en spoiler, men cæsarchiffer er ingen reell måte å kryptere en melding på.[9]
Vigenèrechiffer bruker en utvidelse av cæsarchiffer. Her legges det inn et nytt skift for hver bokstav som skal kodes. Skiftlengden styres av et repetert kodeord, en nøkkel. Dersom lengden av kodeordet er like lang som meldingen selv og i seg selv en tilfeldig rekkefølge av bokstaver, ikke blir avslørt og benyttes kun en gang, så er dette et chiffer med en engangsnøkkel. Et slikt chiffer er uknekkelig. Å gjennomføre en slik kryptering i praksis er imidlertid nær uoppnåelig. Dersom det benyttes et kodeord som er kortere enn meldingen vil dette kunne introdusere sykliske mønster som kan avsløres med avanserte statistiske metoder innen frekvensanalyse.[10]
I april 2006 ble mafia sjefen Bernardo Provenzano avslørt og arrestert i sitt skjulested på Sicilia. Dette delvis på bakgrunn av at noen av hans meldinger ble snappet opp. De var skrevet i en form for cæsarchiffer. Provenzano erstattet bokstavene med tall slik at en "A" ble erstattet med "4", "B" med "5" osv.[11]
I 2011 ble Rajib Karim dømt i Storbritannia for planlegging av terror etter at han hadde kommunisert med islamske aktivister i Bangladesh der de hadde diskutert anslag for å sprenge fly fra British Airways og å forstyrre deres datanettverk. Selv om gruppen hadde tilgang til metoder med en betydelig høyere sikkerhet, valgte de å bruke sitt eget chiffer implementert i Microsoft Excel. Karim benyttet selv PGP for å lagre informasjon på sin egen harddisk, men «siden dette chifferet var kjent av kaffirer, eller ikke-troende, ville dette chifferet være mindre sikkert».[12]
| Dekrypterings skift |
Mulig klartekst |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
Et cæsarchiffer kan enkelt knekkes, endog om en kun har tilgang til chiffertekst. To situasjoner er tenkbare:
Det første tilfellet er det vanskeligste. Gitt at en har tilgang til tilstrekkelig med chiffrert tekst kan en benytte frekvensanalyse på bokstaver og på ord.[13] Ut fra resultatene er det trolig at analytikeren snart innser at chfferet trolig er et cæsarchiffer.
I det andre tilfellet over er det trivielt å knekke chifferet. Siden det er et begrenset antall skift som er mulig (26 i engelsk, 29 i norsk og 24 i latin), kan en enkelt gjennomføre et brute force angrep.[14]
En måte å gjennomføre dette på er å skrive ut en utsnitt av chifferteksen i en tabell med alle mulige skift.[15] [16] I eksempelet er benyttet chifferteksten "EXXEGOEXSRGI". Ved å lete ned gjennom tabellen finner en straks at med et skift på fire får en en meningsfull klartekst: attackatonce (angripumiddelbart). En annen tilnærming er å skrive ut alfabetet på papirremser. Remsene organiseres vertikalt og forskyves slik at en i en av linjene stiller inn chifferteksten. I en av de andre linjene vil da klarteksten fremkomme.
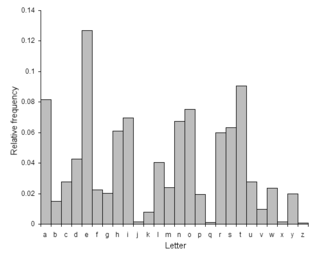
En annen brute forcemetode er å benytte freksvensanalyse. Ved å tegne et stolpediagram av forekomsten av de enkelte bokstavene i chifferteksten og sammenligne dette diagrammet med et tilsvarende diagram for forekomsten av bokstavene i klartekstspråket vil en umiddelbart se hvilken forskyvning som er benyttet. For eksempel i engelsk språk er bokstavene E og T de som med høyest forekomst, mens Q og Z opptrer sjeldent.[17]
Datamaskiner kan enkelt programmeres til å gjøre slike sammenligninger.[18]
I de fleste tilfeller vil en nær umiddelbart finne den mest plausibel klarteksten, dog kan særlig korte meldinger gi tvetydighet som: MPQY kan bety "aden" or "know (gitt at klarteksten er i engelsk). Med tilgang til mer chiffertekst vil denne usikkerheten forsvinne.
I mange chiffer vil en kunne øke sikkerheten ved å gjenta gjennomløpe krypteringen flere ganger. Dette fordi en førte chiffrering med skift shift n og deretter en ny chiffrering med skift m vil tilsvare en enkelt chiffrering med n + m.[19]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
