Stelling van Kuratowski

In de grafentheorie, een deelgebied van de wiskunde, is de stelling van Kuratowski een karakterisering van planaire grafen. De stelling is genoemd naar Kazimierz Kuratowski, die in 1930 voor het eerst een bewijs ervan publiceerde^[1].

Terminologie

Planariteit

Een graaf, die bestaat uit knopen en bogen, kan op verschillende manieren op een plat vlak worden getekend. Een graaf is planair als hij in het euclidische vlak kan worden getekend zonder dat de bogen elkaar kruisen (behalve bij de knopen). Het kan zijn dat dezelfde graaf ook met kruisende bogen getekend kan worden, maar dat maakt niet uit.

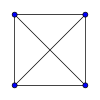
Hierboven staan twee manieren om de volledige graaf met vier knopen op het platte vlak te tekenen. Aangezien de bogen van de rechter elkaar niet kruisen, gaat het hier om een planaire graaf, hoewel de graaf ook met elkaar kruisende bogen getekend kan worden.

Subdivisies

Een subdivisie van een graaf is die graaf waarin bogen door paden van willekeurige lengte zijn vervangen.

	${\displaystyle \Rightarrow }$
De rechter graaf is een subdivisie van de linker.

Volledige grafen

${\displaystyle K_{n}}$ is de volledige graaf met ${\displaystyle n}$ knopen, en ${\displaystyle K_{m,n}}$ is de volledige bipartiete graaf waarvan de eerste partitie ${\displaystyle m}$ en de tweede ${\displaystyle n}$ knopen heeft. De volledige grafen die een rol spelen in de stelling van Kuratowski zijn ${\displaystyle K_{5}}$ en ${\displaystyle K_{3,3}}$.

De volledige graaf ${\displaystyle K_{5}}$	De volledige bipartiete graaf ${\displaystyle K_{3,3}}$

Stelling

De stelling van Kuratowski luidt:

Een graaf is planair, dan en slechts dan als hij geen subgraaf bevat die isomorf is met een subdivisie van ${\displaystyle K_{5}}$ of van ${\displaystyle K_{3,3}}$.^[2]

In het vervolg noemen we een subgraaf die isomorf is met een subdivisie van ${\displaystyle K_{5}}$ of ${\displaystyle K_{3,3}}$ een Kuratowski-subgraaf.

Het gaat hier om een karakterisering van planaire grafen: grafen die een Kuratowski-subgraaf bevatten zijn niet planair, en geen enkele planaire graaf bevat een Kuratowski-subgraaf.

Voorbeeld

In de volgende afbeelding wordt met behulp van de stelling van Kuratowski bewezen dat de graaf die een hypercubus representeert, niet planair is:

In de bovenste figuur wordt een subdivisie van ${\displaystyle K_{5}}$ als subgraaf aangegeven, terwijl in de onderste een subdivisie van ${\displaystyle K_{3,3}}$ aangegeven wordt.

Verwante stellingen

• De stelling van Kuratowski is nauw verwant met de stelling van Wagner, die in 1937 door Klaus Wagner werd bewezen. De stelling van Wagner luidt dat een graaf planair is, dan en slechts dan als ${\displaystyle K_{5}}$ en ${\displaystyle K_{3,3}}$ geen minoren ervan zijn. Het is makkelijk in te zien dat een graaf een minor is van zijn subdivisies, en bovendien dat een subgraaf van een graaf ook een minor van die graaf is. Als ${\displaystyle G}$ dus een subdivisie van ${\displaystyle H}$ als subgraaf bevat, dan bevat ${\displaystyle G}$ de graaf ${\displaystyle H}$ ook als minor. Andersom kan men ook aantonen, dat elke graaf die ${\displaystyle K_{5}}$ of ${\displaystyle K_{3,3}}$ als minor bevat, ook een Kuratowski-subgraaf heeft. Daarom kan men een bewijs van de ene stelling gebruiken om ook de andere te bewijzen.^[2]
• De wiskundige Karl Menger heeft ook in 1930 een soortgelijke stelling bewezen voor grafen waarin alle knopen de orde drie hebben. Het is in dat geval een nodige en voldoende voorwaarde dat er in ${\displaystyle G}$ geen subgraaf voorkomt die isomorf is met een subdivisie van ${\displaystyle K_{3,3}}$.

Bronnen, noten en/of referenties

1. (fr) Kuratowski, Casimir (1930). Sur le problème des courbes gauches en topologie. Fund. Math. 15: 271–283. DOI: 10.4064/fm-15-1-271-283.
2. (en) Bondy, J. A., Murty, U.S.R. (2008). Graph Theory. Springer. ISBN 9781846289699.