Попречен бран

Напречен бран (трансверзален бран) — бран чии колебања се нормални на насоката на движење на бранот. За разлика од ова, надолжниот бран патува во насока на неговите колебања. Водните бранови се пример за попречен бран.

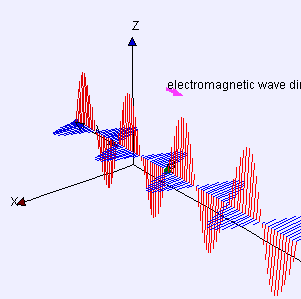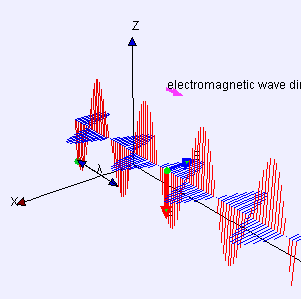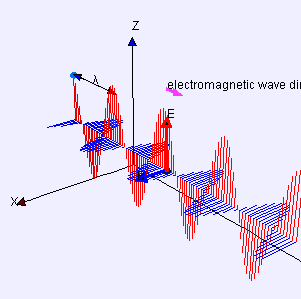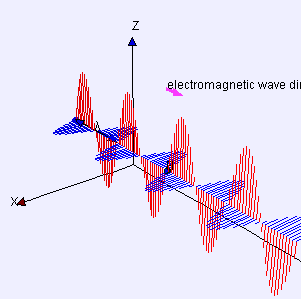
Thumb — Илустрација на прост (рамнински) попречен бран како се движи низ растеглива средина во хоризонтален правец, а четичките се поместуваат во вертикален. Прикажан е само еден слој материјал.

Прост пример за попречни бранови е кога земаме хоризонтално јаже, го врзуваме едниот крај за нешто, а другиот го мафтаме горе-долу. Друг пример се брановите создадени од опната на еден тапан. Брановите патуваат во насоки кои се напоредни на рамнината на опната, но секоја точка на самата опна се поместува нагоре и надолу, нормално на таа рамнина. Светлината е уште еден пример за попречен бран, чии колебања се во електричните и магнетните полиња, под прав агол на идеалните светлински зраци кои го опишуваат правецот на движење.

Попречните бранови често се јавуваат кај растегливи цврсти материи поради создаденото смолкнување; колебањата во овој случај се поместувањето на честичките од нивната мирна положба во правци нормални на брановото патување. Овие поместувања одговараат на смолкнувачко изобличување на материјалот. Затоа, попречен бран од овој карактер се нарекува смолкнувачки бран. Бидејќи флуидите не можат да се спротивстават на смолкнувачки сили додека се во мирување, движењето на попречните бранови во флуидната маса е невозможно.^[1] In сеизмологијата, смолкнувачките бранови се нарекуваат и вторични бранови или S-бранови.

Попречните бранови се разликуваат од надолжни бранови, каде колебањата одвиват во насоката на бранот. The standard example of a надолжен бран е звучниот бран или „притисочен бран“ во гасовите, течностите и цврстите материи, чии колебања предизвикуваат збивање и ширење на материјалот низ кои се движи бранот. Притисочните бранови се нарекуваат и „првични бранови“ или „P-бранови“ во геофизиката.

Математички изразено, најпростиот вид на попречен бран е рамнинскииот линеарно полазиран синусоиден бран. „Рамнината“ тука значи дека правецот на движење е неменлив и останува ист низ целата средина; „линеарно поларизиран“ значи дека правецот на поместување исто така е неменлив и насекаде ист; величината на поместувањето е синусоидна функција само на времето и положбата долж правецот на брановото патување.

Движењето на ваквиот бран може да се изрази математички на следниов начин. Ако d е насоката на движење (вектор со единична должина), а o е било која упатна точка во средината. Нека u биде правецот на колебањата (уште еден вектор со единична должина нормален на d). Поместувањето на честичка во секоја точа p на средината во секое време t (секунди) би било $S(p,t)=Au\sin \left({\frac {t-(p-o){\frac {d}{v}}}{T}}+\phi \right)$ при што A е замавот или силата на бранот, T е неговиот период, v е брзината на движење, а φ е неговата фаза во o. Сите овие параметри се реални броеви. Симболот „•“ го означува внатрешниот производ на два вектора.

Со оваа равенка, бранот патува во правецот d, а колебањата се одвиваат долж правецот u. Бранот е линеарно поларизиран во правецот u.

Набљудувачот кој гледа во неподвижна точка p ќе ја види тамошната честичка во просто хармонично (синусоидно) движење со период од T секунди, и најголемо поместување A во секоја смисла; т.е. со честота f = 1/T полни циклуси на колебање во секоја секунда. Ако ги застанеме сите честички во еден миг t ќе го видиме истото поместување за сите честички на секоја рамнина нормална на d, при што поместувањата во последователни рамнини ќе образуваат синусоида, а секој полн циклус ќе се протега долж d со брановата должина λ = v T = v/f. Целата шема се движи во правецот d со брзина V.

Истата равенка опшишува рамнински линеарно полазиран синусоиден светлински бран, освен што „поместувањето“ S(p, t) е електричното поле во точка p и време t. (Магнетното поле би се опишало со истата равенка, но со правец на „поместување“ кој е нормален на d и u, и различен замав.)

Начело на суперпозиција

Во еднородна линеарна средина, сложените колебања (треперењата во текови на материјал или светлина) можат да се опишат како суперпозицијата на многубројни прости синосоидни бранови, било попречни или надолжни.

На пример, треперењата на виолинска жица може да се анализираат како збир на многу попречни бранови со различни честоти кои ја поместуваат жицата горе-долу или лево-десно. Бранчињата во бара може да се анализираат како комбинација од попречни и надолжни бранови (гравитациски бранови) кои се движат заедно.

Кружна поларизација

Ако средината е линеарна и овозможува повеќекратни независни правци на поместување за истиот правец на патување d, можеме да избереме две заемно нормални правци на поларизација и да го изразиме било кој бран линеарно поларизиран во секој друг правец како линеарна комбинација (мешање) на тие два брана.

Комбинирајќи два брана со иста честота, брзина и правец на движење, но со различни фази и независни правци на поместување, добиваме кружно или елиптично поларизиран бран. Кај таков бран честичките опишуваат кружни или елиптични траектории наместо да се движат напред-назад.

Корисна е илустрацијата со јажето, но овојпат крајот го мафтаме лево-десно наместо горе-долу. Има две независни (правоаголни) правци во кои може да се движат брановите. (Ова важи за секои две насоки под прав агол — горе-долу и лево-десно се избрани како поедноставни.) Секој бран создаден со мафтање на раката во права линија ќе биде линеарно поларизиран бран.

Но доколку раката ја движиме кружно, движењето создава спирален бран на жицата. Раката тогаш се движи истовремено горе-долу и лево-десно. Максимите на движењето лев-десно се достигнува една четвртина бранова должина (или четвртина од кругот, 90° или π/2 радијани) од максимите на движењето горе-долу. Во секоја точка долж јажето, неговото поместување ќе ја опише истата кружница како вашата рака, но со задоцнување во вредност од брзината на патување на бранот. Кружните движења налево или надесно даваат бранови со лева или десна кружна поларизација.

При рачно мафтање, кружниците што ги опишува раката нема да бидат совршени, што води до елиптично поларизирани бранови. Во краен случај елипсата станува права линија, што дава линеарна поларизација долж големата оска на елипсата. Елиптичното движење секогаш може да се разложи на две правоаголни линеарни движења од нееднаков замав и 90 степени вон фаза, при што кружната полариација е посебен случај каде двете линеарни движења имаат точно ист замав.

Моќ на попречен бран во жица

(Нека густината на линеарната маса на жицата биде μ.)

Кинетичката енергија на масен елемент во попречен бран е: $dK={\frac {1}{2}}\ dm\ v_{y}^{2}={\frac {1}{2}}\ \mu dx\ A^{2}\omega ^{2}\cos ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)$

Во една бранова должина, кинетичката енергија $K={\frac {1}{2}}\mu A^{2}\omega ^{2}\int _{0}^{\lambda }\cos ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)dx={\frac {1}{4}}\mu A^{2}\omega ^{2}\lambda$

Користејќи го Хуковиот закон, потенцијалната енергија во масениот елемент $dU={\frac {1}{2}}\ dm\omega ^{2}\ y^{2}={\frac {1}{2}}\ \mu dx\omega ^{2}\ A^{2}\sin ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)$

И потенцијалната енергија за една бранова должина $U={\frac {1}{2}}\mu A^{2}\omega ^{2}\int _{0}^{\lambda }\sin ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)dx={\frac {1}{4}}\mu A^{2}\omega ^{2}\lambda$