Линеарна функција

Не треба да се поистоветува со Линеарна равенка.

Постојат повеќе дефиниции за линеарна функција во светот.

• Линеарна функција се дефинира како полиномна функција од прв степен од една независно променлива х ^[1][2], од што следува дека:
  • Во експлицитен облик имаме:   ${\displaystyle f(x)=ax+b}$  или  ${\displaystyle y(x)=ax+b}$  или  ${\displaystyle y=ax+b,\,a\neq 0}$.
  • Бидејќи тука а≠0, опаѓаат константни функции (хоризонтални прави) и остануваат само коси прави во рамнината.
  • Оваа дефиниција има природно место помеѓу константна функција и квадратна функција.

Линеарна функција

• Линеарна функција се дефинира како функција чиј графикон е права во рамнина ^[3][4], од што следува дека:
  • Во експлицитен облик имаме:   ${\displaystyle f(x)=ax+b}$  или  ${\displaystyle y(x)=ax+b}$  или  ${\displaystyle y=ax+b}$.
  • Во оваа дефиниција се вклучени и хоризонтални прави y=b, односно константни полиноми. (Вертикални прави x=b не се функции.)
  • Забелешка: оваа дефиниција е без условот a≠0.

---

• Потоа, во линеарна аглебра понекогаш се користи изразот линеарна функција за поимот линеарно пресликување.
  • Линеарно пресликување е пресликување f со услов дека f(ax+by)=af(x)+bf(y).
  • Како комбинација на сите погорни дефиниции во одредени места се дефинира линеарна функција како функција: у(x)=ax, т.е. права која врви низ (0,0).^[5]

---

Во Р Македонија најчесто се користат првите дефиниции, односно линеарна функција е функција чиј графикон е права (или коса права).

Забелешка: Честопати наизменично се користат термините линеарна равенка и линеарна функција, но тие не се исти термини. Линеарна функција е линеарна равенка, но обратното не важи. (При линеарна равенка, зборот линеарна се однесува на степенот на полиномот кој може да има 1,2,3,... променливи така да линеарна равенка во една променлива е точка на бројната оска, линеарна равенка во две променливи е права во рамнина, линеарна равенка во три променливи е рамнина во простор.) Види линеарна равенка.

Три линеарни функции во експлицитен облик (црвената и кафеавата го имаат истиот наклон (коефициент на правец, градиент, косина), а црвената и зелената ја имаат истата пресечна точка со у-оската.

Основни својства

Коефициентите a и b се константи, односно при работа се заменуваат со конкретни реални броеви, а остануваат x и y како променливи. На пример: у(x) = -x+2 е линеарна функција со a=-1 и b=2. Множеството на допуштени вредности на секоја линеарна функција е R, т.е. сите реални броеви. Значи, било кој реален број може да „влезе“ во линеарна функција, односно да биде замената за х во функцијата. Сликата, т.е. множеството на сите излезни вредности исто така е R, т.е. сите реални броеви.

Формално, функција, f:R→R дефинирана со f(x) = ax+b каде што a,b∈R е линеарна функција. Линеарна функција е 1-1 бијективна функција.

Правата која е графиконот на линеарна функција е множеството на сите точки: (x,y(x)). Поради тоа што две точки определуваат една права, при графичко претставување на линеарна функција, доволно е да се заменува две различни вредности за x во линеарната функција, да се пресметаат двете вредности на y, соодветните точки (x₁,y(x₁)) и (x₂,y(x₂)) да се внесат во рамнината и права да се црта низ нив.^[6]

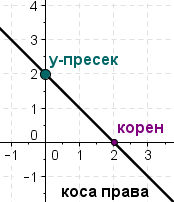
Линеарна функција има точно еден пресек со у-оската во точката (0,b) и (доколку е коса права, a≠0) точно еден пресек со х-оската во точката (^-b⁄_a,0). Вредноста x=^-b⁄_a е единствениот корен на функцијата y=ax+b, т.е е единственото решение на равенката ax+b=0.

Има три облици на линеарна функција: стандарден облик, експлицитен облик и вектор - параметарски облик

Примена на линеарна функција - Пример: Брзина v како функција на време t на предмет истрелан директно нагоре со почетна брзина v₀ се опишува со линеарната функција: v(t)= -9,81t+v₀  [m/s], каде што -9,81  [m/s²] e гравитациска константа. Тука времето t ја игра улогата на независно променливата х, а брзината v е зависно променливата y.

Стандарден облик

Стандарден облик

   ${\displaystyle Ax+By=C,\,B\neq 0}$   (додатен услов за коса права:  ${\displaystyle A\neq 0}$  ).

Овој облик се користи најповеќе во геометрија и во системи на две линеарни равенки во две непознати. Стандарден облик има 2 променливи x и у и 3 константни, т.е. коефициенти A, B, и C кои однапред се заменуваат со реални броеви. На пример: 3x-2y=1. Константите A, B, и C не се еднозначно определени. Ако се множат со фактор k, коефициентите се менуваат, но правата останува истата. На пример: правите 3x-2y=1 и 6x-4y=2 ја претставуваат истата права. Тука факторот k=2.

Експлицитен облик

Експлицитен облик

   ${\displaystyle y(x)=ax+b}$  или  ${\displaystyle y=ax+b}$   (додатен услов за коса права:     ${\displaystyle {a\neq 0}}$  ).

Експлицитен облик има 2 променливи x и у и 2 константни, т.е. коефициенти а и b кои унапред се заменуваат со реални броеви. На пример: y(х)=-2х+4. Константите a и b се уникатни (еднозначно определени), т.е. ако било кој од a или b се менува, правата се менува. Ова значи дека секоја линеарна функција може да се пиши на единствен начин во експлицитен облик.

Константниот коефициент b е т.н. у-пресек, односно точката (0,b) е точката каде што правата врви низ у-оската. Бројот ^-b⁄_а е т.н. корен на функцијата, односно точката (^-b⁄_а,0) е точката каде што правата врви низ х-оската.

Коефициентот а е т.н. наклон или коефициент на правец или градиент или косина на правата и ја опишува брзината на промена на функцијата у во однос на променливата х.

• Наклонот на линеарна функција у(x)=ax+b е константен и е еднаков на a.
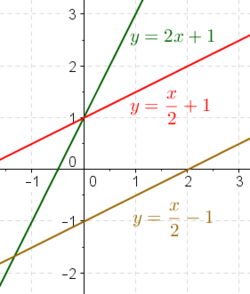
• Ако наклонот на две прави е ист, правите или се паралелни или се совпаѓаат.
• Ако наклонот на една права е a, тогаш за било која точка (х,у) на правата, точката (х+1, y+a) лежи на правата. (Види слика надесно.)
• Ако наклонот a>0 тогаш линеарната функција монотоно расте, ако a&lt0 тогаш функцијата монотоно опаѓа. Ако |a|<1 тогаш наклонот е благ, а ако |a|>1 тогаш наклонот е остар.^[7]

Пример: y(x)=-2x+4. Тука a=-2 и b=4. Имаме (0,b)=(0,4) е пресекот на правата со у-оската, (^-b⁄_а,0)=(^-4⁄_-2,0)=(2,0) e пресекот на правата со х-оската и а = -2 е наклонот на правата, односно за секој чекор х=1 надесно, у се менува за -2 односно слегува надолу.

Во математичката дисциплина диференцијално сметање (калкулус) е дефиниран поимот извод, а извод на една функција ја мери брзината на промена на една променлива во однос на друга во секоја точка. Кај линеарна функција брзината на промената на у во односно на х е константна, т.е. иста во сите точки, односно е а за сите (реални) вредности х, и пишуваме изводот на у(x)=ax+b постои секаде и е константната функција у'(x)=a.

'Вектор - параметарски облик

Параметарски облик

Параметарски: ${\displaystyle \left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.}$    или

Векторски: ${\displaystyle {\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})}$  или  ${\displaystyle r(t)=<x_{1}+a_{1}t,\,y_{1}+a_{2}t>,\,{a_{1}\neq 0}}$    (додатен услов за коса права:   ${\displaystyle {a_{2}\neq 0}}$  ).^[8][9]

Вектор-параметарски облик (или само параметарски облик) има 1 параметар t, 2 променливи x и у, и 4 константни, т.е. коефициенти а₁, а₂, x₁, и y₁. Константите а₁, а₂, x₁, и y₁ не се уникатни (еднозначно определени). Правата врви низ точките А=(x₁,y₁) и B=(x₁+a₁,y₁+a₂) така да земајќи други две точки на истата права ќе резултира во различни константни за истата права. Со вектор-параметарски облик едноставно се дефинира отсечката ${\displaystyle {\overline {AB}}}$ ограничувајќи го параметарот t∈[0,1]. На ваков начин се моделира патувањето по права линија од една точка до друга во времето. Исто така едноставно овој облик се проширува за права во простор. Обичајно е инженери да ја користат буквата t за параметарот; математичари да ја користат буквата λ.

Пример: X=(-1,1)+t(2,3). Тука: a₁=2, a₂=3, x₁=-1 и y₁=1. Правата врви низ точката (x₁,y₁)=(-1,1) и точката (x₁+a₁,y₁+a₂)=(1,4). Соодветниот параметарски облик на оваа права е: x(t)=-1+2t, y(t)=1+3t. Експлицитен облик на оваа права е: y(x)=1,5x+2,5   (решејќи ја првата равенка по t и заменувајќи го резултатот во втората равенка). Една форма на стандарден облик за оваа права е: -3x+2y=5.

Формули за равенки на линеарна функција

За формулите за равенка на права види права.

Литература

1. http://www.sparknotes.com/math/precalc/polynomialfunctions/section1.rhtml
2. „архивски примерок“ (PDF). Архивирано од изворникот (PDF) на 2016-03-25. Посетено на 2013-06-24.
3. Clapham, Nicholson (1990) Oxford Concise Dictionary of Mathematics, pp.480
4. Gelfand, Glagoleva, Shnol (2002) Functions and Graphs
5. http://www.unizor.com/Doc/zor_math_teen_algebra_FL_function_linear.html
6. „архивски примерок“. Архивирано од изворникот на 2013-03-02. Посетено на 2013-06-21.
7. http://www.shodor.org/interactivate/activities/SlopeSlider/
8. http://tutorial.math.lamar.edu/Classes/CalcIII/EqnsOfLines.aspx
9. „архивски примерок“. Архивирано од изворникот на 2013-06-27. Посетено на 2013-06-21.

Други наводи

• http://web.cortland.edu/matresearch/OxfordDictionaryMathematics.pdf
• http://emathforall.com/wiki/RecnikT/LinearnaFunkcija Архивирано на 2 март 2013 г. (на македонски со видео објаснување)
• http://www.shodor.org/interactivate/activities/SlopeSlider/ (на англиски со интерактивност)
• http://www.cut-the-knot.org/Curriculum/Calculus/StraightLine.shtml (на англиски со интерактивност)

Поврзани теми

• Права (геометрија)
• Полином
• Константна функција
• Квадратна функција
• Линеарна равенка

• Портал: Математика