Двоичен броен систем

Двоичен броен систем (бинарен броен систем) — броен систем што изразува бројчени вредности користејќи два симболи: 0 и 1, обично по пат на положбен запис (нотација) со основа 2. Овој систем е од суштинско значење кај сите современи сметачи, заради неговата примена во секое дигитално струјно коло со логички порти.

Бројни системи кај разни народи и култури
Индоарапски броеви
Западноарапски • Источноарапски
Бенгалски • Гуџаратски • Гурмухски • Деваганарски (Индиски) • Синхалски • Тамилски
Балиски • Бурмански • Ѕонгкански (Бутански) • Јавански • Кмерски • Лаоски • Монголски • Тајландски
Источноазиски броеви
Виетнамски Јапонски Кинески (Суџојски)	Корејски Стапчиња Хокиенски
Азбучни броеви
Абџадски Арјабатини Гиски (Етиопски) Грузиски Грчки	Ерменски Кирилични Римски Хебрејски
Други системи
Атички Брамански Вавилонски Глаголични Егејски Египетски Етрурски Инуитски	Кипу Кхаростенски Мајански Муискански Поле со урни Праисториски Чувашки
Положбени системи по основа
Десетични (10)
1, 2, 3, 4, 5, 6, 8, 12, 16, 20, 30, 36, 60 повеќе…
п р у

Историски, за творец на двоичниот броен систем се смета индискиот математичар Пингала, кој разработил математички начин на претставување на прозодијата. Оттогаш, се вршени различни проучувања и подобрувања на истиот, а во 1679 година, Готфрид Лајбниц дошол до неговиот современ облик, објавувајќи го во написот „Објаснение за двоичната аритметика“ (Explication de l'Arithmétique Binaire). Во него, тој за првпат ги употребил цифрите 0 и 1, исто како во современиот систем.

Еден двоичен број може да се претстави со која било низа на битови (двоични бројки), кои пак можат да се претстават со кој било механизам што може да биде во заемно исклучиви состојби. Бројчената вредност зависи од вредноста што ја претставуваат симболите. Кај еден сметач бројчените вредности може да се претстават со два различни напона; кај магнетниот складиштен диск може да се користат магнетните поларитети. Вредностите „позитивно“, „да“ или „вклучено“ не мора да соодветствуваат на бројната вредност еден. Тоа зависи од осмислената архитектура.

Историја

Индискиот мислител Пингала (V-II век п.н.е.) разработил математички начин на претставување на прозодијата, и така го осмислил првиот двоичен броен систем.^[1][2] Пингала користел двоични броеви во облик на кратки и долги согласки (со должина колку две кратки), и со тоа разработил систем сличен на Морзеовата азбука.^[3][4]

Во древна Кина се знаело за збир од осум триграми („ба гуа“) и збир од 64 хексаграми преку класичното дело „И чинг“ („Книга на промените“), што е аналогно на трибитни и шестбитни двоични бројки. Во XI век, мислителот Шао Јунг разработил метод на подредување на хексаграмите што соодветствува на низата од 0 до 63 во двоичниот систем, каде јин претставувал 0, а јанг претставувал 1, со најмал значенски бит врз нив. Меѓутоа нема докази дека Шао имал сознанија за двоичните пресметки. Редоследот е исто така лексикографски редослед од шесткратни варијанти на елементи одбрани од двоелементно множество.^[5]

Слични двоични претстави се користеле и во Африка, во системите за претскажување како „ифа“, како и кај западната средновековна геомантија. Системот на претскажување со основа 2 наоѓал широка примена во Потсахарска Африка со векови.

Во 1605 година, англискиот мислител Френсис Бејкон објавил труд во кој објаснува дека буквите од азбуката можат да се сведат на низи од двоични цифри, кои потоа може да се шифрираат како едвај видливи варијации пред некој неповрзан текст.^[6] Од големо значење за општата теорија на двоично шифрирање е неговата идеја дека овој метод може да се примени користејќи какви било предмети: „под услов овие предмети да се разликуваат само двозначно; како со ѕвона, со труби, со светла и факли, со истрели од пушки и други предмети од таков карактер“.^[6]

Во 1679 година, Готфрид Лајбниц го проучувал двоичниот систем, доаѓајќи до неговиот современ облик во написот „Објаснение за двоичната аритметика“ (Explication de l'Arithmétique Binaire) (1703)^[7]. Во неговиот систем, Лајбниц користи 0 и 1, исто како во современиот систем. Лајбниц бил синофил и бил фасциниран од „И чинг“ каде хексаграмите соодветствуваат на двоичните броеви од 0 до 111111, и заклучил дека ова е доказ за големите достигнувања на Кинезите во полето на филозофската математика.^[8]

Двоични бројки (код) на марка на Македонска пошта по повод Самитот за информатичко општество 2004 (ФДЦ 15/2004, 16 октомври 2004)

Во 1854, британскиот математичар Џорџ Бул го објавил неговиот епохален труд во кој образложува алгебарски систем во логиката, подоцна наречен „Булова алгебра“. Неговата логичка анализа одиграла суштинска улога во осмислувањето на дигиталните кола.^[9]

Во 1937 г, Клод Шенон го објавил својот магистерски труд на Масачусетскиот технолошки институт (МТИ) каде за првпат во историјата се објаснува примената на Буловата алгебра и двоичната аритметика кај електронските релеи и прекинувачи. Со овој труд, насловен како „Симболична анализа на кола со релеи и прекинувачи“ (A Symbolic Analysis of Relay and Switching Circuits), Шенон ги поставил основите на практичната конструкција на дигитални кола.^[10]

Во ноември 1937 г, Џорџ Штибиц како вработен во Беловите лаборатории (Bell Labs), изработил сметач со релеи кој го нарекол „Модел К“ („кујна“, собата кајшто го склопувал), кој вршел пресметки по пат на двоично собирање.^[11] Во 1938 година, Беловите лаборатории започнале полна истражна програма предводена од Штибиц. На 8 јануари 1940 година го изработиле сметачот Complex Number Computer („Сметач на комплексни броеви“) кој можел да пресметува комплексни броеви. На научниот собир на Американското математичко друштво во колеџот Дартмур, на 11 септември 1940 година Штибиц демонстрирал далечинско давање на наредби на сметачот со телепринтер поврзан преку телефонска линија. Ова е првата сметачка машина што можела да се управува од далечина преку телефонска линија. Присутни на собирот биле Џон фон Нојман, Џон Мокли и Норберт Винер, кои го овековечиле овој настан во своите мемоари.^[12][13][14]

Претставување

Еден двоичен број може да се претстави со која било низа на битови (двоични бројки), кои пак можат да се претстават со кој било механизам што може да биде во заемно исклучиви состојби. Еве различни низи од симболи што можат да се протолкуваат како двоична бројчена вредност на бројот 667:

1 0 1 0 0 1 1 0 1 1
| − | − − | | − | |
x o x o o x x o x x
д н д н н д д н д д

Двоичен часовник со светлечки диоди за изразување на двоичните вредности. На овој часовник, секоја колона диоди прикажува двоично шифриран десетичен број од вообичаеното шеесетеречно време.

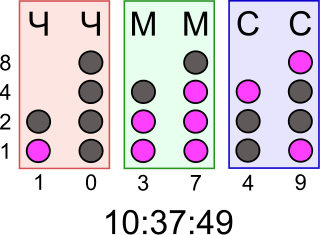
Бројчената вредност во сите четири случаја зависи од вредноста што ја претставуваат симболите. Кај еден сметач бројчените вредности може да се претстават со два различни напона; кај магнетниот складиштен диск може да се користат магнетните поларитети. Вредностите „позитивно“, „да“ или „вклучено“ не мора да соодветствуваат на бројната вредност еден. Тоа зависи од осмислената архитектура.

Поради распространетата употреба на арапските бројки, двоичните броеви по обичај се пишуваат со симболите 0 и 1. При нивно запишување, двоичните бројки честопати имаат долен индекс, претставка или наставка, со цел да се укаже на нивната основа. Следниве записи имаат истоветно значење:

100101 двоично (јасен исказ на форматот)

100101b (наставка што означува двоичен формат)

100101B (наставка што означува двоичен формат)

bin 100101 (претставка што означува двоичен формат)

100101₂ (долен индекс што означува двоичен запис, т.е. на основа 2)

%100101 (претставка што означува двоичен формат)

0b100101 (претставка што означува двоичен формат, доста застапен во програмските јазици)

Во усното општење, двоичните бројки се читаат цифра по цифра, за да се разликуваат од десетичните броеви. На пример, двоичниот број 100 се изговара „еден нула нула“, а не „сто“. Двоичната бројка 100 е еднаква на десетичната вредност четири, и затоа не би било исправно бројката да се нарече „сто“.

Броење во двоичниот систем

Десетично	Двоично
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
16	10000

Броењето во двоичниот систем е слично на она во другите бројни системи. Почнувајќи од една цифра, го набројуваме секој симбол, во растечки редослед. Десетичното пребројување се врши со симболите од 0 до 9, додека двоичниот ги користи само симболите 0 и 1.

Кога ќе се потрошат симболите за првата цифра, следната најголема цифра (лево) се накачува, и броиме пак од 0. Во десетичниот систем броењето оди вака:

000, 001, 002, ... 007, 008, 009, (најдесната бројка станува прва, а следната бројка се накачува)

010, 011, 012, ...

   ...

090, 091, 092, ... 097, 098, 099, (најдесните две бројки стануваат први, а следната бројка се накачува)

100, 101, 102, ...

Откако цифра ќе достигне 9, со накачување се враќа на 0 но исто така предизвикува накачување на следната бројка лево од неа. Броењето во двоичниот систем е исто, освен тоа што се користат само симболите 0 и 1. Така, откако цифрата ќе достигне 1, со накачување се враќа 0, но исто така предизвикува накачување на следната бројка лево од неа:

0000,

0001, (најдесната бројка станува прва, а следната бројка се накачува)

0010, 0011, (најдесните две бројки стануваат први, а следната бројка се накачува)

0100, 0101, 0110, 0111, (најдесните три бројки стануваат први, а следната бројка се накачува)

1000, 1001, ...

Бидејќи двоичниот систем е систем на основа 2, секоја цифра претставува растечки степен на 2 - најдесната цифра претставува 2⁰, следната претставува 2¹, па 2², итн. За да ја утврдиме десетичната претстава на еден двоичен број, едноставно го земаме збирот од производите на двоичните цифри и степените на 2 што ги претставуваат. На пример двоичниот број:

100101

можеме да го претвориме во десетичен облик со:

[(1) × 2⁵] + [(0) × 2⁴] + [(0) × 2³] + [(1) × 2²] + [(0) × 2¹] + [(1) × 2⁰] =

[1 × 32] + [0 × 16] + [0 × 8] + [1 × 4] + [0 × 2] + [1 × 1] = 37

За да создадеме поголеми броеви, едноставно додаваме уште цифри на левата страна од двоичната претстава.

Двоични дропки

Двоичните дропки имаат крај само ако именителот има 2 како единствен примфактор. Така, 1/10 нема конечен двоичен израз, и поради тоа 10 × 0,1 не е еднакво на точно 1 во аритметиката со променливи децимали. На пример, ако сакаме да го протолкуваме двоичниот израз 1/3 = ,010101..., ова значи: 1/3 = 0 × 2⁻¹ + 1 × 2⁻² + 0 × 2⁻³ + 1 × 2⁻⁴ + ... = 0,3125 + ... Не може да се најде точната вредност со збир од конечен број на обратни основи два, а нулите и единиците се редат наизменично до бесконечност.

Дропка	Десетична	Двоично	Дробна апрокс.
1/1	1 или 0,999...	1 или 0,111...	1/1 или 1/2+1/4+1/8...
1/2	0,5 или 0,4999...	0,1 или 0,0111...	1/2 или 1/4+1/8+1/16...
1/3	0,333...	0,010101...	1/4+1/16+1/64...
1/4	0,25 или 0,24999...	0,01 или 0,00111...	1/4 или 1/8+1/16+1/32...
1/5	0,2 или 0,1999...	0,00110011...	1/8+1/16+1/128...
1/6	0,1666...	0,0010101...	1/8+1/32+1/128...
1/7	0,142857142857...	0,001001...	1/8+1/64+1/512...
1/8	0,125 или 0,124999...	0,001 или 0,000111...	1/8 или 1/16+1/32+1/64...
1/9	0,111...	0,000111000111...	1/16+1/32+1/64...
1/10	0,1 или 0,0999...	0,000110011...	1/16+1/32+1/256...
1/11	0,090909...	0,00010111010001011101...	1/16+1/64+1/128...
1/12	0,08333...	0,00010101...	1/16+1/64+1/256...
1/13	0,076923076923...	0,000100111011000100111011...	1/16+1/128+1/256...
1/14	0,0714285714285...	0,0001001001...	1/16+1/128+1/1024...
1/15	0,0666...	0,00010001...	1/16+1/256...
1/16	0,0625 или 0,0624999...	0,0001 или 0,0000111...	1/16 или 1/32+1/64+1/128...

Двоична аритметика

Двоичната аритметика е иста како аритметиката на останатите бројни системи. Со двоичните бројки може да се врши собирање, одземање, множење и делење.

Собирање

Електрична шема на еден двоичен полусуматор кој собира два бита, давајќи збир со преносни битови.

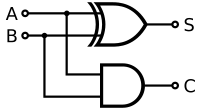
Најпростата двоична аритметичка операција е собирањето. Собирањето на два едноцифрени двоични броја е релативно просто, користејќи облик на пренос:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 10, пренесуваме 1 (бидејќи 1 + 1 = 0 + 1 × двоично 10)

Со собирање на две цифри „1“ ја добиваме цифрата „0“, а 1 треба да се собере во следната колона. Ова е слично на постапката кај десетичниот систем кога се собираат дадени едноцифрени броеви. Ако резултатот е еднаков или поголем од вредноста на основата (10), цифрата лево се накачува:

5 + 5 → 0, пренесуваме 1 (бидејќи 5 + 5 = 0 + 1 × 10)

7 + 9 → 6, пренесуваме 1 (бидејќи 7 + 9 = 6 + 1 × 10)

Ова се нарекува „пренос“. Кога збирот ја надминува вредноста на една цифра, тогаш го „пренесуваме“ лево вишокот износ поделен со основата (т.е. 10/10), собирајќи го со следната положбена вредност. Ова е исправно бидејќи следната положба има тежина што е повисока за фактор еднаков на основата. Преносот кај двоичните операции се врши на истиот начин:

  1 1 1 1 1  (пренесени бројки)
    0 1 1 0 1
+   1 0 1 1 1
-------------
= 1 0 0 1 0 0

Во овој пример собираме две бројки: 01101₂ (13₁₀) и 10111₂ (23₁₀). Во најгорниот ред стојат употребените преносни битови. Почнувајќи од најдесната колона, 1 + 1 = 10₂. 1 се пренесува лево, а најдолу во најдесната колона се пишува 0. Повторно се собира втората колона од десно: 1 + 0 + 1 = 10₂; 1 се пренесува, а најдолу се пишува 0. Третата колона: 1 + 1 + 1 = 11₂. Овојпат, се пренесува 1, и во најдолниот ред се пишува 1. По оваа постапка го добиваме конечниот резултат 100100₂ (36 десетично).

Кога сметачот треба да собере два броја, правилото: x ексили y = (x + y) мод 2 за кои било два бита x и y исто така овозможува многу брза пресметка.

Многу проблеми при двоичното собирање се упростуваат со методот на долг пренос наречен и „Брукхаусов метод на двоично собирање“. Овој метод е корисен кај секое двоично собирање каде еден од броевите има долга низа од цифри „1“. Следниве големи двоични броеви се собираат во два едноставни чекора без повеќекратни преноси од едно место на следното.

  1 1 1   1 1 1 1 1   (пренесени бројки)                   (метод на долг пренос)
    1 1 1 0 1 1 1 1 1 0                              1 1 1 0 1 1 1 1 1 0
+   1 0 1 0 1 1 0 0 1 1            Наспроти:       +   1 0 1 0 1 1 0 0 1 1  најпрвин ги собираме прецртаните бројки
-----------------------                          + 1 0 0 0 1 0 0 0 0 0 0  = збир на прецртаните бројки
= 1 1 0 0 1 1 1 0 0 0 1                          -----------------------  потоа ги собираме преостанатите бројки
                                                   1 1 0 0 1 1 1 0 0 0 1

Во овој пример додаваме две бројки: 1 1 1 0 1 1 1 1 1 0₂ (958₁₀) и 1 0 1 0 1 1 0 0 1 1₂ (691₁₀). Во најгорниот ред стојат употребените преносни битови. Наместо стандардниот пренос од една колона во следната, може да се собере единицата („1“) со најмала положбена вредност со „1“ во соодветната положбена вредност под неа, а „1“ може да се пренесе една цифра по крајот на низата. Овие броеви мора да се прецртаат бидејќи се веќе собрани. Потоа едноставно го собираме резултатот со непрецртаните цифри во вториот ред. По оваа постапка го добиваме конечниот резултат 1 1 0 0 1 1 1 0 0 0 1₂ (1649₁₀).

Таблица на собирање

Дијаграм со значењата на четвороцифрените броеви за секое од следниве: без знак, знак и величина, дополнување на единица и дополнување на двојка. Во денешната дигитална електроника наоѓаат примена само без знак и дополнувањето на двојка.

	0	1
0	0	1
1	1	10

Двоичната таблица на собирање е слична, но не иста како таблицата на вистинитост на дисјунктивната операција ${\displaystyle \lor }$. Разликата се состои во тоа што ${\displaystyle 1\lor 1=1}$, додека пак ${\displaystyle 1+1=10}$.

Одземање

Одземањето работи на истиот начин:

0 − 0 → 0

0 − 1 → 1, позајмуваме 1

1 − 0 → 1

1 − 1 → 0

Ако ја одземеме цифрата „1“ од цифрата „0“ добиваме „1“, а пак 1 ќе треба да се одземе од следната колона. Ова се нарекува „позајмување“ и работи исто како преносот. Ако резултатот од одземањето е помал од 0 (најмалата можна вредност на една цифра), тогаш го „позајмуваме“ недостатокот поделен со основата (т.е. 10/10) од лево, одземајќи го од следната положбена вредност.

    *   * * *   (позајмуваме од колоните со ѕвездички)
  1 1 0 1 1 1 0
−     1 0 1 1 1
----------------
= 1 0 1 0 1 1 1

Одземањето на позитивен број е истоветно на „собирање“ на негативен број со еднаква апсолутна вредност. Сметачите користат запис со дополнување на двојка за да претстават негативни вредности. Со овој запис се избегнува потребата од посебно „одземање“. Користејќи запис со дополнување на двојка одземањето може накратко да се претстави во следнава формула:

А − Б = А + не Б + 1

Множење

Двоичното множење е слично на неговиот десетичен пандан. Два броја А и Б можат да се помножат со делумни производи: за секоја цифра во Б, производот на таа цифра во А се пресметува и се пишува во нов ред, се пренесува лево така што неговата најдесна цифра се порамнува со цифрата што се користела во Б. Збирот од сите овие делумни производи го дава конечниот резултат.

Бидејќи во двоичниот систем постојат само две цифри, постојат само два можни исхода од делумното множење:

• Ако цифрата во Б е 0, и делумниот производ ќе биде 0
• Ако цифрата во Б е 1, делумниот производ е еднаков на А

На пример, двоичните броеви 1011 и 1010 се множат вака:

           1 0 1 1   (А)
         × 1 0 1 0   (Б)
         ---------
           0 0 0 0   ← Соодветствува на нула во Б
   +     1 0 1 1     ← Соодветствува на единица во Б
   +   0 0 0 0 
   + 1 0 1 1 
   ---------------
   = 1 1 0 1 1 1 0

Двоичните броеви можат и да се помножат со битови по двоична запирка:

               1 0 1,1 0 1   (А) (5,625 десетично)
             × 1 1 0,0 1     (Б) (6,25  десетично)
             -------------
                   1,0 1 1 0 1   ← Соодветствува на единица во Б
     +           0 0,0 0 0 0     ← Соодветствува на нула во Б
     +         0 0 0,0 0 0
     +       1 0 1 1,0 1
     +     1 0 1 1 0,1
     -----------------------
     =   1 0 0 0 1 1,0 0 1 0 1   (35,15625 десетично)

Таблица на множење

	0	1
0	0	0
1	0	1

Двоичната таблица множење е иста со вистинитосната таблица на операцијата со логичкиот сврзник ${\displaystyle \land }$.

Делење

Двоичното делење е исто така слично на неговиот десетичен пандан:

Овде, делителот е 101₂ или 5 десетично, додека деленикот е 11011₂, or 27 десетично. Постапката е иста како кај десетичното разложено делење; тука делителот 101₂ оди во првите три цифри 110₂ на деленикот еднаш, и така „1“ се пишува во најгорниот ред. Овој резултат се множи со делителот, и се одзема од првите три цифри на деленикот. Се вклучува следната цифра („1“) за да се добие нова трицифрена низа:

              1
        ___________
1 0 1   ) 1 1 0 1 1
        − 1 0 1
          -----
            0 1 1

Потоа постапката се повторува со новата низа, така продолжувајќи додека не се потрошат цифрите во деленикот:

             1 0 1
       ___________
1 0 1  ) 1 1 0 1 1
       − 1 0 1
         -----
           0 1 1
         − 0 0 0
           -----
             1 1 1
           − 1 0 1
             -----
               1 0

Вака, деленикот на 11011₂ поделен со 101₂ е 101₂, како што (во најгорниот ред), додека остатокот (во најдолниот ред) е 10₂. Во десетичниот систем, 27 поделено со 5 е 5 со остаток 2.

Битови операции

Главна статија: Битова операција

Иако не се во непосредно сродство со бројченото толкување на двоичните симболи, битовите низи може да се манипулираат користејќи ги Буловите логички оператори. Ваквата манипулација со низа двоични симболи се нарекува битова операција. Логичките оператори И, ИЛИ и ЕКСИЛИ може да се применат врз соодветните битови во две двоични бројки наведени како извод. Логичката операција НЕ може да се примени врз поединични битови во една двоична бројка наведена како извод. Понекогаш ваквите операции се користат како аритметички кратенки, а може да понудат и други пресметковни предности. На пример, ако извршиме аритметичко поместување лево на еден двоичен број е исто како да сме го помножиле со (позитивна, интегрална) основа 2.

Претворање од и во други бројни системи

Десетично

За да претвориме цела бројка на основа 10 во двоична бројка на основа 2, го делиме бројот со два, а остатокот е најмалиот значенски бит. Резултатот (цел број) повторно се дели со два, а остатокот е следниот најголем значенски бит. Оваа постапка ја повторуваме сè додека не добиеме резултат нула.

Претворањето од основа 2 на основа 10 се врши со обратна примена на горенаведениот логаритам. Битовите во двоичниот број се користат еден по еден, започнувајќи од најголемиот значенски (најлев) бит. Почнувајќи од вредноста 0, ја удвојуваме претходната вредност и го додаваме следниот бит за да ја добиеме следната вредност, повторувајќи ја постапката. Ова може да се организира во табела со повеќе колони. На пример, ако сакаме да го претвориме 10010101101₂ во десетичен систем:

Претходна вредност	× 2 +	Следен бит	Следна вредност
0	× 2 +	1	= 1
1	× 2 +	0	= 2
2	× 2 +	0	= 4
4	× 2 +	1	= 9
9	× 2 +	0	= 18
18	× 2 +	1	= 37
37	× 2 +	0	= 74
74	× 2 +	1	= 149
149	× 2 +	1	= 299
299	× 2 +	0	= 598
598	× 2 +	1	= 1197

Резултатот е 1197₁₀. Првата претходна вредност на 0 е едноставно првична десетична вредност. Овој метод е примена на т.н. Хорнерова шема.

Двоично	1	0	0	1	0	1	0	1	1	0	1
Десетично	1×210 +	0×29 +	0×28 +	1×27 +	0×26 +	1×25 +	0×24 +	1×23 +	1×22 +	0×21 +	1×20 =	1197

Дробните делови на еден број се претвораат на сличен начин. И тие се засноваат на еквивалентноста на префрлањето со удвојувањето или располовувањето.

Како имаме дробен двоичен број како ,11010110101₂, првата цифра е ${\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}}$, втората е ${\displaystyle {\begin{matrix}({\frac {1}{2}})^{2}={\frac {1}{4}}\end{matrix}}}$, итн. Така, ако имаме 1 на првото место по децималната запирка, тогаш бројот е барем ${\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}}$ и обратно. Двапати тој број изнесува барем 1. Ова укажува на алгоритамот: бројот што треба да се претвори постојано го удвојуваме, и кога резултатот е барем 1, го исфрламе целобројниот дел.

На пример, ${\displaystyle {\begin{matrix}({\frac {1}{3}})\end{matrix}}}$₁₀ двоично претставен е:

Претворање	Резултат
${\displaystyle {\begin{matrix}{\frac {1}{3}}\end{matrix}}}$	0,
${\displaystyle {\begin{matrix}{\frac {1}{3}}\times 2={\frac {2}{3}}<1\end{matrix}}}$	0,0
${\displaystyle {\begin{matrix}{\frac {2}{3}}\times 2=1{\frac {1}{3}}\geq 1\end{matrix}}}$	0,01
${\displaystyle {\begin{matrix}{\frac {1}{3}}\times 2={\frac {2}{3}}<1\end{matrix}}}$	0,010
${\displaystyle {\begin{matrix}{\frac {2}{3}}\times 2=1{\frac {1}{3}}\geq 1\end{matrix}}}$	0,0101

Одовде, повторливата десетичната дропка 0,3... е истоветна со повторливата двоична дропка 0,01... .

На пример, 0,1₁₀, двоично ќе биде:

Претворање	Резултат
0,1	0,
0,1 × 2 = 0,2 < 1	0,0
0,2 × 2 = 0,4 < 1	0,00
0,4 × 2 = 0,8 < 1	0,000
0,8 × 2 = 1,6 ≥ 1	0,0001
0,6 × 2 = 1,2 ≥ 1	0,00011
0,2 × 2 = 0,4 < 1	0,000110
0,4 × 2 = 0,8 < 1	0,0001100
0,8 × 2 = 1,6 ≥ 1	0,00011001
0,6 × 2 = 1,2 ≥ 1	0,000110011
0,2 × 2 = 0,4 < 1	0,0001100110

Ова е и повторлива двоична дропка 0,00011... . Може да нè изненади тоа што конечните десетични дропки може да имаат повторливи разложувања во двоичниот систем. Од оваа причина, многумина се изненадуваат кога ќе увидат дека 0,1 + ... + 0,1 (10 собирања) се разликува од 1 во аритметиката со променливи децимали. Впрочем, единствените двоични дропки со разложувања што имаат завршеток се оние со облик на цел број поделен со основа 2, а 1/10 не е таква дропка.

Конечното претворање е од двоични во десетични дропки. Тешкотии се јавуваат само при работа со повторливи дропки, а инаку методот е да ја префрлиме дропката во цел број, да го извршиме горенаведеното претворање, а потоа да го поделиме со соодветниот степен на 2 во десетичната основа. На пример:

${\displaystyle x}$	=	1100	,101110...
${\displaystyle x\times 2^{6}}$	=	1100101110	,01110...
${\displaystyle x\times 2}$	=	11001	,01110...
${\displaystyle x\times (2^{6}-2)}$	=	1100010101
${\displaystyle x}$	=	(789/62)10

Друг начин на претворање од двоичен во десетичен систем, воедно побрз ако сме запознаени со шеснаесетеречниот систем, е непосредното претворање—прво да го претвориме (${\displaystyle x}$ двоично) во (${\displaystyle x}$ шеснаесетеречно), а потоа да го претвориме (${\displaystyle x}$ шеснаесетеречно) во (${\displaystyle x}$ десетично).

Овие прости методи не се погодни за работа со многу големи броеви бидејќи со нив вршиме голем број на множења или делења каде еден операнд е исклучително голем. Позгоден начин е да употребиме алгоритам раздвојувајќи го бројот: ако имаме двоичен број, го делиме на 10^k, каде k го одбираме така што количникот е приближно еднаков на остатокот, а потоа секој дел го претвораме во десетичен систем и двата дела ги конкатенираме. Ако имаме десетичен број, можеме да го разделиме на два дела со приближно еднаква големина, па секој од нив го претвораме во двоичен систем, каде првиот претворен дел го множиме со 10^k и го собираме со вториот претворен дел, каде k е бројот на десетични бројки во вториот, најмал значенски дел пред претворањето.

Шеснаесетеречен броен систем

0hex	=	0dec	=	0oct		0	0	0	0
1hex	=	1dec	=	1oct		0	0	0	1
2hex	=	2dec	=	2oct		0	0	1	0
3hex	=	3dec	=	3oct		0	0	1	1
4hex	=	4dec	=	4oct	0	1	0	0
5hex	=	5dec	=	5oct	0	1	0	1
6hex	=	6dec	=	6oct	0	1	1	0
7hex	=	7dec	=	7oct	0	1	1	1
8hex	=	8dec	=	10oct	1	0	0	0
9hex	=	9dec	=	11oct	1	0	0	1
Ahex	=	10dec	=	12oct	1	0	1	0
Bhex	=	11dec	=	13oct	1	0	1	1
Chex	=	12dec	=	14oct	1	1	0	0
Dhex	=	13dec	=	15oct	1	1	0	1
Ehex	=	14dec	=	16oct	1	1	1	0
Fhex	=	15dec	=	17oct	1	1	1	1

Двоичниот систем се претвора во и од шеснаесетеречен (хексадецимален) систем донекаде полесно. Причината е што основата на шеснаесетеречниот систем (16) е степен на основата на двоичниот систем (2). Поконкретно, 16 = 2⁴, па затоа ни треба четири двоични цифри за претставување на една цифра од шеснаесетеречниот систем, како што може да се види на таблицата десно.

Ако сакаме да претвориме еден шеснаесетеречен број во неговиот двоичен еквивалент, едноставно ги заменуваме соодветните двоични цифри:

3A₁₆ = 0011 1010₂

E7₁₆ = 1110 0111₂

За да претвориме еден двоичен број во неговиот шеснаесетеречен еквивалент, го делиме во грпи од по четири бита. Ако бројот на битови не е содржател на четири, едноставно вметнуваме уште битови 0 лево (наречени постава). На пример:

1010010₂ = 0101 0010 групирани со постава = 52₁₆

11011101₂ = 1101 1101 групирани = DD₁₆

За да претвориме еден шеснаесетеречен број во неговиот десетичен еквивалент треба да го помножиме десетичиоот еквивалент на секоја шеснаесетеречна цифра со соодветниот степен на основа 16 и да ги собереме добиените вредности:

C0E7₁₆ = (12 × 16³) + (0 × 16²) + (14 × 16¹) + (7 × 16⁰) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,383₁₀

Октален броен систем

Двоичните износи лесно се претвораат и во октални, бидејќи окталниот користи основа 8, што е степен на основа два (имено, 2³, па така ни требаат точно три двоични цифри за да претставиме некоја октална бројка). Соодветството помеѓу двоичните и окталните бројки е исто како за првите осум цифри од шеснаесетеречен систем во таблицата погоре. Двоичното 000 е исто што и окталното 0, двоичното 111 е исто што и окталното 7, итн.

Октално	Двоично
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Претворањето од октален во двоичен систем се врши исто како за шеснаесетеречниот:

65₈ = 110 101₂

17₈ = 001 111₂

Од двоичен во октален систем:

101100₂ = 101 100₂ групирани = 54₈

10011₂ = 010 011₂ групирани со постава = 23₈

Од октален во десетичен систем:

65₈ = (6 × 8¹) + (5 × 8⁰) = (6 × 8) + (5 × 1) = 53₁₀

127₈ = (1 × 8²) + (2 × 8¹) + (7 × 8⁰) = (1 × 64) + (2 × 8) + (7 × 1) = 87₁₀

Претставување на реални броеви

Нецелите броеви можат да се претстават по пат на негативни основи, кои се одделуваат од останатите бројки со основна запирка (наречена децимална запирка во десетичниот систем). На пример, двоичниот број 11,01₂ ќе биде:

1 × 21	(1 × 2 = 2)	плус
1 × 20	(1 × 1 = 1)	плус
0 × 2−1	(0 × ½ = 0)	плус
1 × 2−2	(1 × ¼ = 0,25)

За збир од 3,25 десетично.

Сите дијадни рационални броеви ${\displaystyle {\frac {p}{2^{a}}}}$ имаат завршна двоична бројка — двоичната претстава има конечен број на членови по основната запирка. Другите рационални броеви имаат двоична претстава, но не завршуваат, туку се повторуваат со конечна последователна низа од бројки што се повторуваат до бесконечност. На пример

${\displaystyle {\frac {1_{10}}{3_{10}}}}$ = ${\displaystyle {\frac {1_{2}}{11_{2}}}}$ = 0,0101010101...₂

${\displaystyle {\frac {12_{10}}{17_{10}}}}$ = ${\displaystyle {\frac {1100_{2}}{10001_{2}}}}$ = 0,10110100 10110100 10110100...₂

Појавата каде двоичната претстава на секој рационален број или завршува или се повторува се јавува и во другите бројни системи што работат со основа. Друга сличност е постоењето на алтернативни претстави за секоја конечна претстава, поради на фактот што 0,111111... е збир на геометриската низа 2⁻¹ + 2⁻² + 2⁻³ + ... што изнесува 1.

Двоичните бројки што ниту завршуваат, ниту се повторуваат претставуваат ирационални броеви. На пример,

• 0,10100100010000100000100.... има шема, но ова не е повторлива шема со постојано иста должина, па затоа бројот е ирационален
• 1,0110101000001001111001100110011111110... е двоична претстава на бројот ${\displaystyle {\sqrt {2}}}$, квадратниот корен од 2, уште еден ирационален број. Овој број нема видлива шема.

Претворачи и пресметувачи

• Претворач на сите видови двоични броеви (вклучувајќи броеви по IEEE754 со единична и двојна прецизност) (англиски)
• Претворач на бројки на која било основа^{[мртва врска]} (англиски)
• Двоичен пресметувач - врши собирање, одземање, множење и делење (англиски)

Поврзано

• Греев код
• Надоместочен двоичен код
• Двоично шифриран десетичен број
• Дополнување на двојка

Наводи

1. Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming : the microchip PIC. Boca Raton, Florida: CRC Press. стр. 37. ISBN 0-8493-7189-9.
2. W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
3. Двоичните броеви во древна Индија (англиски)
4. Математика за поети и тапанари Архивирано на 16 јуни 2012 г. (PDF, 145 КБ) (англиски)
5. Ryan, James A. (1996). „Leibniz' Binary System and Shao Yong's "Yijing"“. Philosophy East and West. University of Hawaii Press. 46 (1): 59–90. doi:10.2307/1399337. JSTOR 1399337. |access-date= бара |url= (help)
6. Бејкон, Френсис. „Напредување во учењето“. Лондон. стр. Глава 1. (англиски)
7. Leibniz G., Explication de l'Arithmétique Binaire, Die Mathematische Schriften, уред. C. Gerhardt, Берлин 1879, том 7, стр. 223; англиски превод
8. Aiton, Eric J. (1985). Leibniz: A Biography. Taylor & Francis. стр. 245–8. ISBN 0-85274-470-6.
9. Boole, George (2009) [1854]. Иследување на законитостите на мислата на кои се темели математичките теории во логиката и веројатноста (Macmillan, Dover Publications, препечатено со исправки [1958]. изд.). Њујорк: Cambridge University Press. ISBN 9781108001533. (англиски)
10. Шенон, Клод Елвуд (1940). Симболична анализа на кола со релеи и прекинувачи. Кембриџ: Масачусетски технолошки институт. (англиски)
11. „Алеја на славните национални изумители – Џорџ Р. Штибиц“. 20 август 2008. Посетено на 5 јули 2010. (англиски)
12. „Џорџ Штибиц: Биогарфија“. Факултет за математика и информатика, Универзитет „Денисон“. 30 април 2004. Посетено на 5 јули 2010. (англиски)
13. „Пионери – Луѓето и идеите кои ги променија нештата – Џорџ Штибиц (1904–1995)“. Кери Редшо. 20 февруари 2006. Посетено на 5 јули 2010. (англиски)
14. „Џорџ Роберт Штибиц – Посмртница“. Здружение за историја на сметачите на Калифорнија. 6 февруари 1995. Посетено на 5 јули 2010. (англиски)

Користена литература

• Sanchez, Julio; Canton, Maria P. (2007), Microcontroller programming : the microchip PIC, Boca Raton, FL: CRC Press, стр. 37, ISBN 0849371899

Надворешни врски

„Двоичен броен систем“ на Ризницата ?

• Двоичен систем и негово претворање во декаден — „Мендо“ (македонски)
• Краток преглед на работата на Лајбниц и двоичните броеви (англиски)
• Двоичен систем на Cut-the-knot (англиски)
• Претворање на дропки на Cut-the-knot (англиски)

Статијата „Двоичен броен систем“ е избрана статија. Ве повикуваме и Вас да напишете и предложите избрана статија (останати избрани статии).