위너 확률 과정

확률 과정 이론에서, 위너 확률 과정(Wiener確率過程, 영어: Wiener stochastic process) 또는 위너 과정(Wiener過程)은 시간차 ${\displaystyle \Delta t}$의 증분의 확률 분포가 평균 0, 분산 ${\displaystyle \Delta t}$의 정규 분포를 이루며, 각 증분이 서로 독립이며, 그 궤적이 거의 확실하게 연속적인 연속 시간 확률 과정이다.

3차원 위너 과정

정의

다음이 주어졌다고 하자.

• 유한 차원 유클리드 공간 ${\displaystyle \mathbb {R} ^{d}}$
• 확률 공간 ${\displaystyle \Omega }$

확률 과정

${\displaystyle (W_{t}\colon \Omega \to \mathbb {R} ^{n})_{t\in [0,\infty )}}$

이 다음 조건들을 만족시킨다면, 위너 확률 과정(영어: Wiener stochastic process)이라고 한다.

• 임의의 ${\displaystyle t\in [0,\infty )}$ 및 ${\displaystyle \Delta t>0}$에 대하여, 확률 변수 ${\displaystyle W_{t+\Delta t}-W_{t}\colon \Omega \to V}$의 확률 분포는 평균이 0이며 분산이 ${\displaystyle t}$인 정규 분포 ${\displaystyle {\mathcal {N}}(0,\Delta t)}$이다.
• (초기 조건) ${\displaystyle \Pr(W_{0}=0)=1}$. 즉, 거의 확실하게 ${\displaystyle W_{0}=0}$이다.
• 임의의 ${\displaystyle 0\leq s\leq t\leq u}$에 대하여, ${\displaystyle W_{u}-W_{t}}$와 ${\displaystyle W_{s}}$는 서로 독립이다.
• ${\displaystyle \Pr(W_{t}\in {\mathcal {C}}^{0}(\mathbb {R} ,V))=1}$. 즉, ${\displaystyle W_{t}}$는 거의 확실하게 연속 함수 ${\displaystyle \mathbb {R} \to V}$를 이룬다. 다시 말해,
  • 임의의 ${\displaystyle \omega \in \Omega }$ 및 임의의 ${\displaystyle \epsilon >0}$ 및 임의의 ${\displaystyle t\in [0,\infty )}$에 대하여, ${\displaystyle \forall s\in (t-\delta ,t+\delta )\colon \|W_{\max\{0,s\}}(\omega )-W_{t}(\omega )\|<\epsilon }$이 되게 하는 양의 실수 ${\displaystyle \delta >0}$가 존재한다.

연산

1차원 위너 확률 과정의 자기 유사성

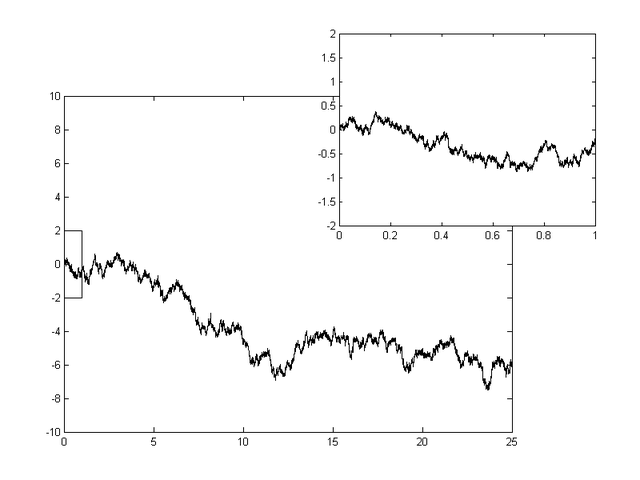
위너 확률 과정 ${\displaystyle (W_{t}\colon \Omega \to \mathbb {R} ^{n})_{t\in [0,\infty )}}$이 주어졌을 때, 확률 과정

${\displaystyle \alpha ^{-1}W_{\alpha ^{2}t}}$

역시 위너 확률 과정을 이룬다. 즉, 그 그래프는 일종의 프랙털을 이룬다.

${\displaystyle W_{t}}$가 유클리드 공간 ${\displaystyle V}$ 값의 위너 확률 과정이라고 하자. 그렇다면, 임의의 부분 벡터 공간 ${\displaystyle V'\leq V}$에 대하여, ${\displaystyle \operatorname {proj} _{V'}W_{t}}$ 역시 ${\displaystyle V'}$ 값의 위너 확률 과정이다.

임의의 직교 행렬 ${\displaystyle M\in \operatorname {O} (V)}$ 및 ${\displaystyle V}$ 값의 위너 확률 과정 ${\displaystyle (W_{t}\colon \Omega \to V)_{t\in [0,\infty )}}$에 대하여, ${\displaystyle MW_{t}}$ 역시 ${\displaystyle V}$ 값의 위너 확률 과정이다.

예

다음이 주어졌다고 하자.

• 확률 공간 ${\displaystyle \Omega }$
• 실수 힐베르트 공간 ${\displaystyle \operatorname {L} ^{2}([0,1],\mathbb {R} )}$의 정규 직교 기저 ${\displaystyle (f_{i}\colon [0,1]\to \mathbb {R} )_{i\in I}}$. 여기서 ${\displaystyle I}$는 임의의 가산 무한 집합이다.
• 서로 독립이며, 평균 0, 분산 1의 정규 분포를 따르는 확률 변수들의 열 ${\displaystyle (X_{i}\colon \Omega \to \mathbb {R} )_{i\in I}}$

그렇다면, 임의의 ${\displaystyle t\in [0,1]}$에 대하여, 급수

${\displaystyle W(t)=\sum _{i\in I}X_{i}\langle 1_{[0,t]}|f_{i}\rangle _{\operatorname {L} ^{2}([0,1],\mathbb {R} )}\in \operatorname {L} ^{2}([0,1],\mathbb {R} )}$

는 (${\displaystyle \operatorname {L} ^{2}([0,1],\mathbb {R} )}$의 거리 위상에서) 수렴한다. (여기서 ${\displaystyle 1_{[0,t]}}$는 폐구간의 지시 함수이다.) 이는 위너 확률 과정의 정의를 거의 확실한 연속성만을 제외하고 모두 만족시킨다.

만약 정규 직교 기저를

${\displaystyle f_{i}(x)={\begin{cases}{\sqrt {2}}\cos(\pi ix)&i\in \{1,2,\dotsc \}\\1&i=0\end{cases}}}$

로 잡는다면, 위 급수가 ${\displaystyle t\in [0,1]}$에 대하여 균등 수렴하는 것을 보일 수 있으며, 이 경우 이 급수는 위너 확률 과정을 이룬다.

역사

노버트 위너의 이름을 땄다.

같이 보기

• 위너 공간
• 프랙탈

외부 링크

• Weisstein, Eric Wolfgang. “Wiener process”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• “Wiener process”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.