ಗಣ ಸಿದ್ಧಾಂತ

ಗಣ ಸಿದ್ಧಾಂತ ಎನ್ನುವುದು ಆಧುನಿಕ ಗಣಿತದಲ್ಲಿ ಅತ್ಯಂತ ಮುಖ್ಯವೂ ಮೂಲಭೂತವೂ ಆದ ಪರಿಕಲ್ಪನೆ (ಸೆಟ್ ಥಿಯೊರಿ). ಗಣವೆಂದರೆ ನಿರ್ದಿಷ್ಟವಾದ ವಸ್ತುಗಳ ಅಥವಾ ಪರಿಕಲ್ಪನೆಗಳ ಒಂದು ಸಮೂಹ ಅಥವಾ ಗುಂಪು ಎಂದು ತಿಳಿಯಬೇಕು. ಗಣದ ಪರಿಕಲ್ಪನೆ ಮೂಲಭೂತವಾಗಿರುವುದರಿಂದ ಇದನ್ನು ಇನ್ನೂ ಸುಲಭವಾದ ಬೇರೆ ಮಾತುಗಳಿಂದ ವರ್ಣಿಸುವುದು ಅಸಾಧ್ಯ. ಏಕೆಂದರೆ ಗಣವನ್ನು ಸಮೂಹ ಎಂದೂ, ಸಮೂಹವನ್ನು ಸಮುಚ್ಚಯ ಎಂದೂ ಮುಂತಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸುತ್ತ ಸಾಗಿದರೆ ನಮ್ಮ ಶಬ್ದಭಂಡಾರ ಎಷ್ಟು ವಿಪುಲವಾಗಿದ್ದರೂ ಸಾಂತವಾಗಿರುವುದರಿಂದ ಯಾವುದೋ ಒಂದು ಘಟ್ಟದಲ್ಲಿ ಗಣ ಎಂಬ ಪದವನ್ನೇ ಮತ್ತೆ ಬಳಸಬೇಕಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಈ ಶಬ್ದವನ್ನು ನಿಖರವಾಗಿ ವ್ಯಾಖ್ಯಿಸುವ ಪ್ರಯತ್ನ ಮೇಲೆ ಹೇಳಿದ ಪದ ಪರಂಪರೆಯಲ್ಲಿ ನಮ್ಮನ್ನು ಚಕ್ರೀಯವಾಗಿ ಒಯ್ಯುತ್ತದೆಯೇ ವಿನಾ ನಿಖರವಾದ ವ್ಯಾಖ್ಯೆಯನ್ನು ನೀಡುವುದರಲ್ಲಿ ಕೊನೆಗೊಳ್ಳುವುದಿಲ್ಲ. ಹೀಗಾಗಿ ಇದರ ಅರ್ಥವನ್ನು ನಮ್ಮ ನಿತ್ಯ ಜೀವನದ ಅನುಭವದ ಆಧಾರದ ಮೇಲೆ ಪ್ರತಿಭಾನದಿಂದಲೇ ಅರಿತುಕೊಳ್ಳಬೇಕು.

ಎರಡು ಗಣಗಳ ಛೇದನವನ್ನು ತೋರಿಸುವ ವೆನ್ ಚಿತ್ರ

ಮೂಲ ಪರಿಕಲ್ಪನೆಗಳು ಮತ್ತು ಸಂಕೇತನ

ಗಣವೆಂದರೆ ನಮ್ಮ ಪ್ರತಿಭಾನಕ್ಕೆ ಅಥವಾ ಮನಸ್ಸಿಗೆ ತೋರುವ ಪರಸ್ಪರ ವಿಶಿಷ್ಟವಾದ ವಸ್ತುಗಳ ಇಲ್ಲವೇ ಅಂಶಗಳ ಸಮೂಹ ಅಥವಾ ಸಮಾಹಾರವೆಂದು ತಿಳಿಯತಕ್ಕದ್ದು ಎಂದು ಜಾರ್ಜ್ ಕ್ಯಾಂಟರ್ ಹೇಳಿದ್ದಾನೆ. ಈತನನ್ನೇ ಗಣ ಸಿದ್ಧಾಂತದ ಜನಕ ಎಂದು ಭಾವಿಸುವುದು ವಾಡಿಕೆ. ಒಂದು ಗಣದೊಳಗಿನ ವಸ್ತು ಅಥವಾ ಅಂಶಗಳಿಗೆ ಆ ಗಣದ ಧಾತುಗಳು (ಎಲಿಮೆಂಟ್ಸ್) ಎಂದು ಹೆಸರು. ಒಂದು ಗಣದಲ್ಲಿ ಇರಬಹುದಾದ ಧಾತುಗಳಿಗೆ ಇನ್ನು ಯಾವ ವಿಧವಾದ ನಿರ್ಬಂಧಗಳೂ ಇರುವುದಿಲ್ಲ.ಉದಾಹರಣೆಗೆ,

A = {ಭಾರತದ ಎಲ್ಲ ಪ್ರಜೆಗಳ ಸಮೂಹ}

ಇದೊಂದು ಗಣ. ಒಂದು ಗಣದಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳನ್ನು ಪುಷ್ಪಾವರಣಗಳ (flower brackets) ಒಳಗೆ ಬರೆಯುವುದು ವಾಡಿಕೆ.^[೧] ಗಣಗಳಿಗೆ ಇನ್ನೂ ಕೆಲವು ಉದಾಹರಣೆಗಳನ್ನು ಮುಂದೆ ಬರೆದಿದೆ:

B = {ಒಬ್ಬ ಹುಡುಗನ ಜೇಬಿನಲ್ಲಿರುವ ವಸ್ತುಗಳು}

N = {1, 2, 3, .....ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳು}

T = {ದತ್ತ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ತ್ರಿಭುಜಗಳು}

ಸಾಧಾರಣವಾಗಿ ಗಣಗಳನ್ನು A, B, C ಮುಂತಾದ ಇಂಗ್ಲಿಷ್ ದೊಡ್ಡ ಅಕ್ಷರಗಳಿಂದಲೂ ಧಾತುಗಳನ್ನು a, b, c, x, y, z ಮುಂತಾದ ಇಂಗ್ಲಿಷ್ ಸಣ್ಣ ಅಕ್ಷರಗಳಿಂದಲೂ ಸೂಚಿಸುವುದು ವಾಡಿಕೆ. A ಒಂದು ಗಣವೂ a ಅದರ ಒಂದು ಧಾತುವು ಆಗಿದ್ದರೆ ಈ ಸಂಬಂಧವನ್ನು a ∈ A ಎಂದು ಬರೆದು ತಿಳಿಸುತ್ತೇವೆ. ಇದನ್ನು a, A ಗೆ ಸೇರಿದೆ ಎಂದು ಓದುತ್ತೇವೆ. p, A ಯ ಧಾತುವಲ್ಲದಿದ್ದಾಗ p ∉ A ಎಂದು ಬರೆಯುತ್ತೇವೆ; ಮತ್ತು p, A ಗೆ ಸೇರಿಲ್ಲ ಎಂದು ಓದುತ್ತೇವೆ.

ಒಂದು ಗಣವನ್ನು ಸೂಚಿಸಬೇಕಾದರೆ ಅದರ ಎಲ್ಲ ಧಾತುಗಳನ್ನೂ ಬರೆದು ಪುಷ್ಪಾವರಣಗಳಲ್ಲಿ, ಅಂದರೆ { }, ಅವನ್ನು ಅಡಕಗೊಳಿಸುವುದು ಒಂದು ಮಾರ್ಗ. ಉದಾಹರಣೆಗೆ {ಸೀಸದ ಕಡ್ಡಿ, ಬಳಪ, ಬುಗುರಿ, ಗೋಲಿ} ಎಂದು ಬರೆದು ಒಬ್ಬ ಹುಡುಗನ ಕಿಸೆಯಲ್ಲಿರಬಹುದಾದ ವಸ್ತುಗಳ ಗಣವನ್ನು ಸೂಚಿಸಬಹುದು. ಆದರೆ ಒಂದು ಗಣದಲ್ಲಿರುವ ಧಾತುಗಳ ಸಂಖ್ಯೆ ಬಲು ದೊಡ್ಡದು ಇಲ್ಲವೇ ಅನಂತವಾದಾಗ ಹೀಗೆ ಬರೆಯುವುದು ಕಷ್ಟ ಸಾಧ್ಯ. ಇದಕ್ಕೆ ಬದಲು ಅನುಕೂಲವಾದ ಬೇರೊಂದು ಮಾರ್ಗವನ್ನು ಅನುಸರಿಸುತ್ತೇವೆ. ಉದಾಹರಣೆಗೆ ಭಾರತದ ಸಮಸ್ತ ಪ್ರಜೆಗಳ ಗಣ A ಯನ್ನು

A = {x | x ಭಾರತದ ಪ್ರಜೆಯಾಗಿರಬೇಕು}

ಎಂದು ಬರೆದು ಸೂಚಿಸಬಹುದು. ಇಲ್ಲಿ x ಎಂಬ ಅಜ್ಞಾತ ಭಾರತದ ಪ್ರತಿಯೊಬ್ಬ ಪ್ರಜೆಗೂ ಅನ್ವಯಿಸುತ್ತದೆ. ಅದರ ಪಕ್ಕದಲ್ಲಿ ನೀಟಗೆರೆಯೊಂದನ್ನು ಎಳೆದು, ಅದರ ಬಲಪಾರ್ಶ್ವದಲ್ಲಿ x ಪಾಲಿಸಬೇಕಾದ ನಿಯಮ ಅಥವಾ ನಿರ್ಬಂಧವನ್ನು ತಿಳಿಸುವ ವಾಕ್ಯವನ್ನು ಬರೆಯುತ್ತೇವೆ. ಈ ವಾಕ್ಯ A ಗೆ ಸೇರಿದ ಧಾತುಗಳನ್ನು ಇನ್ನಿತರ ಎಲ್ಲವುಗಳಿಂದ ಬೇರ್ಪಡಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ y ಒಬ್ಬ ಬ್ರಿಟಿಷ್ ಪ್ರಜೆಯಾದರೆ y ∉ A. ಈ ರೀತಿ ಪ್ರತಿಯೊಂದು ಗಣವನ್ನು ನಿರ್ದಿಷ್ಟವಾಗಿ ನಿರೂಪಿಸಲು ಸಾಧ್ಯವೆಂಬುದು ಗಣ ಸಿದ್ಧಾಂತದ ಒಂದು ಮುಖ್ಯ ತತ್ತ್ವ. ಇದಕ್ಕೆ ನಿರ್ದಿಷ್ಟೀಕರಣ ಆದ್ಯುಕ್ತಿ (ಆಕ್ಸಿಯಂ ಆಫ್ ಸ್ಪೆಸಿಫಿಕೇಶನ್) ಎಂದು ಹೆಸರು. ಇದನ್ನು ನಿಖರವಾಗಿ ಹೀಗೆ ಬರೆಯಬಹುದು: A ಒಂದು ಗಣವೂ, S(x) ಒಂದು ನಿರ್ಬಂಧವೂ ಆಗಿದ್ದರೆ, S(x) ನ್ನು ಪಾಲಿಸುವ A ಯ ಧಾತುಗಳಿಂದಲೇ ಏರ್ಪಟ್ಟ ಒಂದು ಗಣ B ಯು A ಮತ್ತು S(x) ಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತದೆ. ಪ್ರತೀಕಗಳಲ್ಲಿ ಇದನ್ನು

B = {x | x ∈ A, S(x)}

ಎಂದು ಸೂಚಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ

A = N = {1, 2, 3.......}

ಎಂಬುದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣವೂ, S(x) ಎಂಬುದು x ಮೂರರ ಒಂದು ಅಪವರ್ತ್ಯ ಎಂಬ ನಿರ್ಬಂಧವೂ ಆಗಿದ್ದರೆ ಆಗ

B = {x ∈ N | S(x)} = {x ∈ N | x = 3n, n ∈ N} = {3, 6, 9.......}

ಎಂಬ ಗಣ ಆಗುತ್ತದೆ.

ಉಪಗಣಗಳು

A ಮತ್ತು S ಗಳು ಎರಡು ಗಣಗಳಾಗಿದ್ದು A ಯ ಪ್ರತಿಯೊಂದು ಧಾತುವೂ S ಗೆ ಸೇರಿದ್ದರೆ ಎಂದರೆ x ∈ S ಎಂಬ ಸಂಬಂಧ ನಿಲ್ಲುವುದಾದರೆ ಆಗ A ಯು S ನ ಒಂದು ಉಪಗಣವೆಂದು ಹೇಳುತ್ತೇವೆ. ಇದನ್ನು A ⊂ S ಎಂದು ಬರೆಯುತ್ತೇವೆ; ಮತ್ತು A ಯು S ನಲ್ಲಿ (ಉಪಗಣವಾಗಿ) ಇದೆ ಎಂದು ಈ ಚಿಹ್ನೆಯನ್ನು ಓದುತ್ತೇವೆ.

ಉದಾಹರಣೆಗಳು:

1. A ⊂ A ಎಂಬ ಸಂಗತಿ ವ್ಯಾಖ್ಯೆಯಿಂದಲೇ ಸ್ಪಷ್ಟ.
2. E = {2, 4, 6, ....} ಎಂಬ ಸರಿಸಂಖ್ಯೆಗಳ (even numbers) ಗಣ, N = {1, 2, 3......} ಎಂಬ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣದ ಒಂದು ಉಪಗಣ.
3. F = {1, 3, 5......} ಎಂಬ ಬೆಸ ಸಂಖ್ಯೆಗಳ (odd numbers) ಗಣವೂ N ನ ಒಂದು ಉಪಗಣ.

ಎಂದರೆ E ⊂ N ಮತ್ತು F ⊂ N.

1 p ಒಂದು ದತ್ತ ಸಮತಲ

T₂ = {p ಯಲ್ಲಿರುವ ಎಲ್ಲ ಸಮದ್ವಿಭುಜ ತ್ರಿಭುಜಗಳು}, ಮತ್ತು

T = {p ಯಲ್ಲಿರುವ ಎಲ್ಲ ತ್ರಿಭುಜಗಳು}

ಆಗಿದ್ದರೆ ಆಗ T₂ ⊂ T.

A ಯು S ನ ಒಂದು ಉಪಗಣವಾಗಿದ್ದರೆ ಆಗ S ಗಣ A ಯನ್ನು ಉಪಗಣವಾಗಿ ಒಳಗೊಂಡಿದೆ ಎಂದು ಹೇಳುತ್ತೇವೆ; ಮತ್ತು ಈ ಸಂಬಂಧವನ್ನು S ⊃ A ಎಂಬ ಪ್ರತೀಕದಿಂದ ನಿರೂಪಿಸುತ್ತೇವೆ. S ಗೆ A ಯ ಮಾತೃಗಣ ಎಂದು ಹೆಸರು. ಈಗ ⊂ ಮತ್ತು ⊃ ಪ್ರತೀಕಗಳನ್ನು ಪರಸ್ಪರ ವಿಲೋಮವಾದ ಅರ್ಥಗಳಲ್ಲಿ ಉಪಯೋಗಿಸುತ್ತೇವೆ.

ಸಮತೆ

ಒಂದೇ ಧಾತುಗಳನ್ನು ಒಳಗೊಂಡ ಎರಡು ಗಣಗಳು ಪರಸ್ಪರ ಸಮ (mutually equal) ಎನ್ನುತ್ತೇವೆ. ಈ ವ್ಯಾಖ್ಯೆಗೆ ಗಣ ಸಿದ್ಧಾಂತದ ವಿಸ್ತರಣದ ಆದ್ಯುಕ್ತಿ (ಆಕ್ಸಿಯಂ ಆಫ್ ಎಕ್ಸ್‌ಟೆನ್ಷನ್)^[೨][೩] ಎಂದು ಹೆಸರು. A ಮತ್ತು B ಗಳು ಪರಸ್ಪರ ಸಮವಾಗಿದ್ದರೆ A = B ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಈಗ A ಯ ಧಾತುಗಳೆಲ್ಲ B ಯಲ್ಲೂ, B ಯ ಧಾತುಗಳೆಲ್ಲ A ಯಲ್ಲೂ ಇರುವುದರಿಂದ A ⊂ B ಮತ್ತು B ⊂ A; ಮತ್ತು ಹೀಗಿರುವಾಗಲೆಲ್ಲ A = B.

ಹೀಗಾಗಿ A ⊂ B ಆದಾಗ ಮತ್ತು B ⊂ A ಆದಾಗ ಮಾತ್ರ A = B

ಇದನ್ನು ಪ್ರತೀಕಗಳಲ್ಲಿ

A ⊂ B ಮತ್ತು B ⊂ A ⇐⇒ A = B ಎಂದು ಬರೆಯುತ್ತೇವೆ.

ನಿಯಮಗಳು

S ಒಂದು ಗಣವೂ, A, B, C ಗಳು ಅದರ ಕೆಲವು ಉಪಗಣಗಳೂ ಆಗಿರಲಿ. ಈಗ A ⊂ B ಮತ್ತು B ⊂ C ಆಗಿದ್ದರೆ, A ಯ ಎಲ್ಲ ಧಾತುಗಳು B ಯಲ್ಲೂ, B ಯ ಎಲ್ಲ ಧಾತುಗಳು C ಯಲ್ಲೂ ಇರುವುದರಿಂದ, A ಯ ಎಲ್ಲ ಧಾತುಗಳು C ಯಲ್ಲಿ ಇರುತ್ತವೆ. ಆದ್ದರಿಂದ A ⊂ C. ಇದನ್ನು ಪ್ರತೀಕಗಳಲ್ಲಿ A ⊂ B ಮತ್ತು B ⊂ C ⇒ A ⊂ C ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಹೀಗಾಗಿ S ನಲ್ಲಿರುವ ಉಪಗಣಗಳ ⊂ ಮತ್ತು ⊃ ಸಂಬಂಧಗಳು ಮುಂದೆ ಹೇಳಿರುವ ನಿಯಮಗಳನ್ನು ಪಾಲಿಸುತ್ತವೆ:

1. ಪ್ರತಿಫಲನ ನಿಯಮ (reflexive rule) A ⊂ A^[೪]

2. A ⊂ B ಮತ್ತು B ⊂ C ⇒ A ⊂ C (ವಾಹಕ ನಿಯಮ - transitive rule)

3. A ⊂ B and B ⊃ A ⇒ A = B (ವಿರೋಧ ಸಮಾಂಗತೆಯ ನಿಯಮ - anti-symmetry rule)

ಸಂಯೋಗ

A ಮತ್ತು B ಗಳು ಎರಡು ಗಣಗಳಾಗಿದ್ದರೆ ಇವೆರಡರಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳನ್ನು ಸೇರಿಸಿ ಒಂದು ಗಣವನ್ನು ರಚಿಸಬೇಕೆಂಬ ಅಭಿಲಾಷೆ ಸ್ವಾಭಾವಿಕವಾಗಿಯೇ ಮೂಡುತ್ತದೆ. ಇಂಥ ಒಂದು ದೊಡ್ಡ ಗಣದಲ್ಲಿ A ಮತ್ತು B ಗಳೆರಡೂ ಉಪಗಣಗಳಾಗಿರುತ್ತವೆ. ಈಗ ಇದರಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತುವೂ A ಮತ್ತು B ಗಳಲ್ಲಿ ಒಂದಕ್ಕಾದರೂ ಸೇರಿಸಬೇಕಾಗುತ್ತದೆ. ಈ ಅಭಿಪ್ರಾಯವನ್ನು ಸಾರ್ವತ್ರೀಕರಿಸುವ ತತ್ತ್ವಕ್ಕೆ ಸಂಯೋಗದ ಆದ್ಯುಕ್ತಿ (ಆಕ್ಸಿಯಂ ಆಫ್ ಯೂನಿಯನ್) ಎಂದು ಹೆಸರು. ಇದನ್ನು ಅನುಸರಿಸಿದರೆ A ಯಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳನ್ನೂ, B ಯಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳನ್ನೂ ಒಳಗೊಂಡಿರುವ ಒಂದು ಗಣ ಲಭಿಸುತ್ತದೆ. ಈ ಗಣದಲ್ಲಿ A ಮತ್ತು B ಗಳಲ್ಲಿ ಉಭಯಸಾಮಾನ್ಯವಾಗಿರುವ ಧಾತುಗಳನ್ನು ಒಂದು ಸಲ ಮಾತ್ರ ಆಯ್ದಿರುತ್ತೇವೆ. ಹೀಗೆ ಉಂಟಾದ ಹೊಸ ಗಣಕ್ಕೆ A ಮತ್ತು B ಗಳ ಸಂಯೋಗ (ಯೂನಿಯನ್) ಎಂದು ಹೆಸರು. ಪ್ರತೀಕಗಳಲ್ಲಿ A ⋃ B ಎಂದು ಬರೆದು A ಸಂಯೋಗ B ಎಂದು ಓದುತ್ತೇವೆ. ಈಗ A ⋃ B = {x | x ∈ A ಅಥವಾ x ∈ B} ಎಂದು ನಿಖರವಾಗಿಯೂ ಸಂಕ್ಷೇಪವಾಗಿಯೂ ಬರೆಯಬಹುದು.^[೫]

ಈಗ ∑ ಎಂಬುದು A, B, C ಮುಂತಾದ ಗಣಗಳ ಒಂದು ಸಮೂಹವಾದರೆ, ಕನಿಷ್ಠ ಪಕ್ಷ ಈ ಗಣಗಳಲ್ಲಿ ಒಂದಕ್ಕಾದರೂ ಸೇರಿರುವಂಥ ಎಲ್ಲ ಧಾತುಗಳಿಂದಲೇ ಏರ್ಪಟ್ಟ ಒಂದು ಗಣವಿರುತ್ತದೆ, ಎಂದು ಸಂಯೋಗದ ಆದ್ಯುಕ್ತಿ ಹೇಳುತ್ತದೆ.

ಇದನ್ನು ಸೂತ್ರ ${\displaystyle {\frac {\bigcup x}{x\in \Sigma }}}$ ಎಂದು ನಿರೂಪಿಸುತ್ತೇವೆ.

ಉದಾಹರಣೆಗಳು

1. A = {a, b, c, d, k} ಮತ್ತು B = {b, c, d, e, f, k} ಆಗಿದ್ದರೆ ಆಗ A U B = {a, b, c, d, e, f, k}

2. T = ದತ್ತ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ಆಯತಗಳ ಗಣ, S = ಅದರಲ್ಲಿರುವ ಎಲ್ಲ ಚೌಕಗಳ ಗಣ ಆಗಿದ್ದರೆ, ಆಗ T U S = T. ಇಲ್ಲಿ S ⊂ T ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು.

3. E = ಎಲ್ಲ ಸರಿಸಂಖ್ಯೆಗಳ ಗಣ, F = ಎಲ್ಲ ಬೆಸ ಸಂಖ್ಯೆಗಳ ಗಣ ಆಗಿದ್ದರೆ ಆಗ E U F = N. ಇಲ್ಲಿ N ಎಲ್ಲ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ.

ಛೇದನ

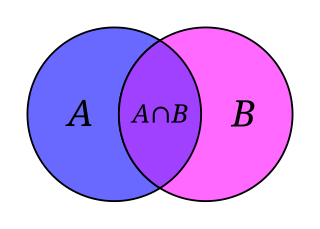
ಈಗ A, B ಗಳು ಎರಡು ಗಣಗಳಾಗಿದ್ದರೆ ಅವೆರಡಕ್ಕೂ ಉಭಯಸಾಮಾನ್ಯವಾಗಿರುವ ಧಾತುಗಳನ್ನೆಲ್ಲ ಸೇರಿಸಿ ಒಂದು ಗಣವನ್ನು ರಚಿಸಬಹುದು.^[೬] ಈ ಗಣವನ್ನು A ಮತ್ತು B ಗಳ ಛೇದನವೆಂದು ಕರೆಯುತ್ತೇವೆ; ಮತ್ತು A ∩ B ಎಂದು ಬರೆಯುತ್ತೇವೆ.^[೭]

ಉದಾಹರಣೆಗಳು

1. A = {a, b, c, d, k} ಮತ್ತು B = {b, c, f, k} ಆಗಿದ್ದರೆ ಆಗ A ∩ B = {b, c, k}

2. T = ದತ್ತ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ಆಯತಗಳ ಗಣ, S = ಅದೇ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ಚೌಕಗಳ ಗಣ ಆಗಿದ್ದರೆ, ಆಗ T ∩ S = S. S ⊂ T ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು.

3. E = ಎಲ್ಲ ಸರಿಸಂಖ್ಯೆಗಳ ಗಣ ಮತ್ತು F = ಎಲ್ಲ ಬೆಸಸಂಖ್ಯೆಗಳ ಗಣ ಆಗಿದ್ದರೆ ಆಗ E ∩ F ನಲ್ಲಿ ಯಾವ ಧಾತುವೂ ಇಲ್ಲ. ಏಕೆಂದರೆ ಪ್ರತಿ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯೂ ಸರಿ ಇಲ್ಲವೇ ಬೆಸ ಆಗಿರುತ್ತದೆ. ಹೀಗಾಗಿ E ಮತ್ತು F ಗಳಿಗೆ ಉಭಯಸಾಮಾನ್ಯವಾದ ಯಾವ ಒಂದು ಸಂಖ್ಯೆಯೂ ಇಲ್ಲ.

ಈ ವಿಶೇಷ ಪರಿಸ್ಥಿತಿಯಲ್ಲೂ E ∩ F ನ್ನು ಒಂದು ಗಣವಾಗಿ ಪರಿಗಣಿಸುತ್ತೇವೆ. ಇದಕ್ಕೆ ಶೂನ್ಯ ಗಣವೆಂದು ಹೆಸರು. ಇದನ್ನು ∅ ಎಂಬ ಚಿಹ್ನೆಯಿಂದ ನಿರೂಪಿಸುತ್ತೇವೆ.

4. ಹೀಗೆಯೇ T ಎಂಬುದು ದತ್ತ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ತ್ರಿಕೋನಗಳ ಗಣವೂ, Q ಎಂಬುದು ಅದೇ ಸಮತಲದಲ್ಲಿರುವ ಎಲ್ಲ ಚತುಷ್ಕೋನಗಳ ಗಣವೂ ಆಗಿದ್ದರೆ ಆಗ T ∩ Q = ∅

ಈ ಶೂನ್ಯ ಗಣ ಪ್ರತಿಯೊಂದು ಗಣಕ್ಕೂ ಒಂದು ಉಪಗಣವಾಗಿದೆಯೆಂದು ಭಾವಿಸುತ್ತೇವೆ. A ಒಂದು ಗಣವಾಗಿದ್ದರೆ A U ∅  = A ಮತ್ತು A ∩ ∅  = ∅ ಎಂದು ಸ್ಪಷ್ಟವಾಗಿ ತಿಳಿದು ಬರುತ್ತದೆ.

A ∩ B = ∅ ಆಗಿದ್ದರೆ ಆಗ A ಮತ್ತು B ಗಳನ್ನು ವಿಯೋಜಿತ ಗಣಗಳೆಂದು ಹೇಳುತ್ತೇವೆ.^[೮]

ವಿಶ್ವಗಣ

ಯಾವುದೇ ಗಣಿತ ವಿಚಾರ ಸರಣಿಯಲ್ಲಿ ಬರುವ ಎಲ್ಲ ಗಣಗಳೂ ಯಾವುದೋ ಒಂದು ಗಣ S ನ ಉಪಗಣಗಳಾಗಿದ್ದರೆ ಈ ವಿಚಾರ ಸರಣಿಯಲ್ಲಿ S ನ್ನು ವಿಶ್ವಗಣವೆಂದು (ಯೂನಿವರ್ಸಲ್ ಸೆಟ್) ಕರೆಯುತ್ತೇವೆ. ಈಗ A ⊂ S ಮತ್ತು B ⊂ S ಆಗಿದ್ದರೆ, ಆಗ A U B ⊂ S ಮತ್ತು A ∩ B ⊂ S. ಈ ವಿಶ್ವಗಣ S ನೊಂದಿಗೆ ಅದರ ಯಾವ ಉಪಗಣ A ಯನ್ನೂ ಸಂಯೋಗ ಮತ್ತು ಛೇದನ ಮಾಡಬಹುದು.

ಇಲ್ಲಿ S U A = S ಮತ್ತು S ∩ A = A ಎಂದು ಸುಲಭವಾಗಿ ತೋರಿಬರುತ್ತದೆ.

ಸಂಯೋಗ ಮತ್ತು ಛೇದನಗಳ ಮುಖ್ಯ ಸಂಬಂಧಗಳು

ಸಂಯೋಗ ಮತ್ತು ಛೇದನಗಳು ಪಾಲಿಸುವ ಮುಖ್ಯ ನಿಯಮಗಳನ್ನು ಇಲ್ಲಿ ಕ್ರೋಡೀಕರಿಸಿದೆ.

ಸಂಯೋಗ

1. A U ∅  = A

2. A U B = B U A (ವ್ಯತ್ಯಯ ನಿಯಮ)

3. A U (B U C) = (A U B) U C (ಸಾಹಚರ್ಯ ನಿಯಮ)

4. A U A =A (ವರ್ಗ ಸಮ ನಿಯಮ – ಐಡೆಂಪೊಟೆಂಟ್ ಲಾ)

5. A ⊂ B ⇐⇒ A U B = B

ಛೇದನ

1. A ∩ ∅  = ∅

2. A ∩ B = B ∩ A (ವ್ಯತ್ಯಯ ನಿಯಮ)

3. A ∩ (B ∩ C) = (A ∩ B) ∩ C (ಸಾಹಚರ್ಯ ನಿಯಮ)

4. A ∩ A = A (ವರ್ಗಸಮ ನಿಯಮ)

5. A ⊂ B ⇐⇒ A ∩ B = A

ವಿತರಣ ನಿಯಮಗಳು

ಸಂಯೋಗ ಮತ್ತು ಛೇದನ ಕ್ರಿಯೆಗಳು ಪರಸ್ಪರವಾಗಿ ವಿತರಣ ನಿಯಮಗಳನ್ನು (ಡಿಸ್ಟ್ರಿಬ್ಯೂಟಿವ್ ಲಾಸ್) ಅನುಸರಿಸುತ್ತವೆ.

A U (B ∩ C) = (A U B) ∩ (A U C)

A ∩ (B U C) = (A ∩ B) U (A ∩ C)

ಸೂಕ್ತವಾದ ವೆನ್ ಚಿತ್ರಗಳನ್ನು ರಚಿಸಿ ಮೇಲಿನ ಎಲ್ಲ ನಿಯಮಗಳನ್ನೂ ತಾಳೆ ನೋಡಬಹುದು.

ಪೂರಕಗಳು (ಕಾಂಪ್ಲಿಮೆಂಟ್ಸ್)

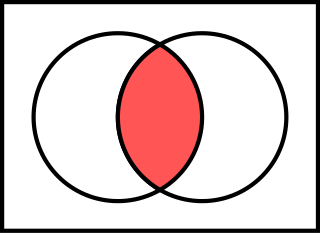
A ಮತ್ತು B ಗಳು ಎರಡು ಗಣಗಳಾದರೆ B ಯಲ್ಲಿದ್ದು A ಯಲ್ಲಿಲ್ಲದ ಎಲ್ಲ ಧಾತುಗಳು ಒಂದು ಗಣವನ್ನು ಏರ್ಪಡಿಸುತ್ತವೆ. ಇದನ್ನು B ಯಲ್ಲಿ A ಯ ಪೂರಕ ಎಂದು ಕರೆಯುತ್ತೇವೆ; ಮತ್ತು B - A ಎಂದು ಬರೆಯುತ್ತೇವೆ.

B - A = {x ∈ B | x ∉ A}

ಚಿತ್ರ (3) ರಲ್ಲಿ B-A ಯನ್ನು ಕೆಂಪು ಬಣ್ಣದಿಂದ ತುಂಬಿಸಿರುವ ಭಾಗ ತೋರಿಸುತ್ತದೆ. ಅದೇ ಚಿತ್ರದಲ್ಲಿ B - A = B - (A ∩ B) ಎಂದು ಸುಲಭವಾಗಿ ತಿಳಿಯುವುದು.

ಚಿತ್ರ (3)

ಈಗ S ವಿಶ್ವಗಣವೂ A ಅದರ ಒಂದು ಉಪಗಣವೂ ಆಗಿದ್ದರೆ, S-A ಯನ್ನು S ನಲ್ಲಿ A ಯ ಪೂರಕವೆಂದು ಹೇಳುವದಕ್ಕೆ ಬದಲು ಸಂಕ್ಷೇಪವಾಗಿ A ಯ ಪೂರಕವೆಂದು ಹೇಳುತ್ತೇವೆ. ಸಾಮಾನ್ಯವಾಗಿ ಇದನ್ನು A' ಎಂಬ ಪ್ರತೀಕದಿಂದ ಸೂಚಿಸುತ್ತೇವೆ.^[೯] ಪೂರಕಗಳು ಪಾಲಿಸುವ ಮೂಲಸಂಬಂಧಗಳನ್ನು ಇಲ್ಲಿ ಬರೆದಿದೆ:

1. (A')' = A

2. ∅' = S

3. S' = ∅

4. A U A' = S

5. A ∩ A' = ∅

6. A ⊂ B ⇒ B' ⊂ A'

7. (A U B)' = A' ⋂ B'

8. (A ⋂ B)' = A' U B'

ಮೇಲಿನ ಪ್ರತಿಯೊಂದು ಸಂಬಂಧವನ್ನೂ ಆಯ್ಲರ್-ವೆನ್ ಚಿತ್ರಗಳ ಮೂಲಕ ಸುಲಭವಾಗಿ ತಿಳಿದುಕೊಳ್ಳಬಹುದು. ಕೊನೆಯ ಎರಡಕ್ಕೆ ಡಿಮಾರ್ಗನ್‌ನ ನಿಯಮಗಳೆಂದು ಹೆಸರು.^{[೧೦][೧೧][೧೨]}

ಸಮಾಂಗ ವ್ಯತ್ಯಾಸ

ಚಿತ್ರ (4)

A ಮತ್ತು B ಎರಡು ಗಣಗಳಾಗಿದ್ದರೆ (A-B) U (B-A) ಗೆ A ಮತ್ತು B ಗಳ ಸಮಾಂಗ ವ್ಯತ್ಯಾಸವೆಂದು ಹೆಸರು.^[೧೩] ಇದನ್ನು A + B ಎಂದು ನಿರೂಪಿಸುತ್ತೇವೆ.

ಎಂದರೆ A + B = (A-B) U (B-A)............(1)

ಚಿತ್ರ (4) ರಲ್ಲಿ ಕೆಂಪು ಬಣ್ಣದಿಂದ ತುಂಬಿರುವ ಭಾಗ (A+B) ಯನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಮೇಲಿನ ಸಮೀಕರಣ (1) ರ ಬಲಭಾಗದಲ್ಲಿ A ಮತ್ತು B ಗಳನ್ನು ಪರಸ್ಪರವಾಗಿ ಪರಿವರ್ತಿಸಿದರೆ ಸಮೀಕರಣ ಬದಲಾಗುವುದಿಲ್ಲ. ಎಂದರೆ A + B = B + A. ಈ ಕಾರಣದಿಂದ A+B ಗೆ ಸಮಾಂಗ (ಸಿಮೆಟ್ರಿಕ್) ಎಂಬ ವಿಶ್ಲೇಷಣ ಚೆನ್ನಾಗಿ ಒಪ್ಪುತ್ತದೆ.

A, B, C ಗಳು ಯಾವ ಮೂರು ಗಣಗಳಾದರೂ (A + B) + C = A + (B + C), A + ∅ = A ಮತ್ತು A + A = ∅  ಎಂದು ಸುಲಭವಾಗಿ ತೋರಿಸಬಹುದು. ಹೀಗಾಗಿ + ಎಂಬ ದ್ವಿಗುಣ ಪರಿಕರ್ಮದಲ್ಲಿ S ವಿಶ್ವಗಣದ ಎಲ್ಲ ಉಪಗಣಗಳೂ ಮುಂದೆ ಪಟ್ಟಿಮಾಡಿರುವ ನಿಯಮಗಳನ್ನು ಪಾಲಿಸುತ್ತವೆ. ಇದರಿಂದ S ನ ಎಲ್ಲ ಉಪಗಣಗಳು ಒಂದು ವ್ಯತ್ಯಯ ಗ್ರೂಪ್ (ಕಾಮ್ಯುಟೇಟಿವ್ ಗ್ರೂಪ್) ಎಂದು ತೋರಿಬರುತ್ತದೆ. ಏಕೆಂದರೆ

1. A, B ⊂ S ಆಗಿದ್ದರೆ ಆಗ A + B ⊂ S.
2. (A + B) + C = A + (B + C) (ಸಾಹಚರ್ಯ ನಿಯಮ)
3. A + B = B + A (ವ್ಯತ್ಯಯ ನಿಯಮ)
4. A + ∅ = A ಎಂದರೆ ಈ ಪರಿರ್ಮಕ್ಕೆ ∅ ಎಂಬುದೇ ಏಕಾಂಶ
5. A + A = ∅, ಎಂದರೆ ಪ್ರತಿಯೊಂದು A ಗೂ ಅದೇ ಗಣ ವ್ಯಸ್ತ (ಇನ್ವರ್ಸ್)

ಘಾತಗಣಗಳು

ಈ ವರೆಗೆ ದತ್ತಗಣ S ನ ಎಲ್ಲ ಉಪಗಣಗಳನ್ನು ಕುರಿತು ಪ್ರಸ್ತಾವಿಸುತ್ತಿದ್ದೆವು. ಇವೆಲ್ಲ ಉಪಗಣಗಳನ್ನೂ ಧಾತುಗಳಾಗಿ ಪಡೆದಿರುವ ಒಂದು ಗಣವುಂಟೇ ಎಂಬ ಪ್ರಶ್ನೆಗೆ ಉತ್ತರ ಮುಂದೆ ಉಕ್ತವಾಗಿರುವ ಧಾತುಗಳ ಆದ್ಯುಕ್ತಿಯಲ್ಲಿ ಸಿಕ್ಕುತ್ತದೆ.

S ಒಂದು ಗಣವಾಗಿದ್ದರೆ ಇದರ ಸಮಸ್ತ ಉಪಗಣಗಳನ್ನೂ ಒಳಗೊಂಡಿರುವ ಒಂದು ಗಣ ಉಂಟು. ಈಗ ಈ ಗಣದಲ್ಲಿ S ನ ಉಪಗಣಗಳೇ ಅಲ್ಲದೆ ಇತರ ಧಾತುಗಳೂ ಇರುವುದಕ್ಕೆ ಅವಕಾಶವಿದೆ. ಈ ತೊಂದರೆಯನ್ನು ನಿವಾರಿಸಲು

P(S) = {‌X | X ⊂ S}

ಎಂದು ವಿಶಿಷ್ಟೀಕರಿಸಿದರೆ P(S) ನಲ್ಲಿ S ನ ಉಪಗಣಗಳು ಮಾತ್ರ ಧಾತುಗಳಾಗಿರುತ್ತವೆ. P(S) ಗೆ S ನ ಘಾತಗಣವೆಂದು ಹೆಸರು.^[೧೪]

ಉದಾಹರಣೆ: S = {1, 2} ಆಗಿದ್ದರೆ ಆಗ

P(S) = { ∅ , {1}, {2}, {1, 2} }

ಹೀಗೆ P(S) ನಲ್ಲಿ 2² ಧಾತುಗಳಿವೆ. ಹೀಗೆಯೇ S ನಲ್ಲಿ n ಧಾತುಗಳಿದ್ದರೆ P(S) ನಲ್ಲಿ 2ⁿ ಧಾತುಗಳಿರುತ್ತವೆ. S ಸಾಂತಗಣವಾಗಿದ್ದರೆ (finite set), P(S) ನಲ್ಲಿರುವ ಧಾತುಗಳ ಸಂಖ್ಯೆ 2 ರ ಒಂದು ಘಾತ (power). ಇಂಥ ಗಣಗಳನ್ನು ಘಾತಗಣಗಳೆಂದು ಕರೆಯುವುದು ಈ ಕಾರಣದಿಂದ.

E ಮತ್ತು F ಗಳು ಯಾವ ಎರಡು ಗಣಗಳಾದರೂ

P(E) ∩ P(F) = P(E ∩ F) ಮತ್ತು

P(E) U P(F) ⊂ P(E U F) ಎಂಬ ಸಂಬಂಧಗಳು ದೊರೆಯುತ್ತವೆ.

ಆಯ್ಲರ್-ವೆನ್ ಚಿತ್ರಗಳು

ಜ್ಯಾಮಿತೀಯ ರೀತಿಯಲ್ಲಿ ಗಣಗಳನ್ನೂ, ಅವುಗಳ ಸಂಯೋಗ, ಛೇದನ ಇತ್ಯಾದಿ ಸಂಬಂಧಗಳನ್ನೂ ಕಣ್ಣಿಗೆ ಕಟ್ಟುವಂತೆ ಚಿತ್ರಗಳ ರೂಪದಲ್ಲಿ ತೋರಿಸುವುದು ವಾಡಿಕೆ. ಇಂಥ ಚಿತ್ರಗಳಿಗೆ ಆಯ್ಲರ್ ಚಿತ್ರಗಳು ಅಥವಾ ವೆನ್ ಚಿತ್ರಗಳು ಎಂದು ಹೆಸರು. ಸಾಮಾನ್ಯವಾಗಿ ವಿಶ್ವಗಣವನ್ನು ಒಂದು ದೊಡ್ಡ ಆಯತ ಪ್ರತಿನಿಧಿಸುವಂತೆಯೂ ಅದರ ಉಪಗಣಗಳನ್ನು ಆಯತದ ಒಳಗಿನ ವೃತ್ತಗಳು ಪ್ರತಿನಿಧಿಸುವಂತೆಯೂ ಚಿತ್ರಿಸುವುದು ವಾಡಿಕೆ.

ಇಲ್ಲಿ ತೋರಿಸಿರುವ ಚಿತ್ರದಲ್ಲಿ S ವಿಶ್ವಗಣ, A ಮತ್ತು B ಅದರ ಎರಡು ಉಪಗಣಗಳು; ಎಂದರೆ A ⊂ S, B ⊂ S. ಚಿತ್ರದಲ್ಲಿ A U B ಯನ್ನು A ಮತ್ತು B ಎರಡನ್ನೂ ನಿರೂಪಿಸುವ ವೃತ್ತಗಳ ಭಾಗಗಳಿಂದ ಆವೃತ್ತವಾಗಿರುವ ಭಾಗ ತೋರಿಸುತ್ತದೆ; ಚಿತ್ರ 1 ರಲ್ಲಿ ಇದನ್ನು ಕೆಂಪು ಬಣ್ಣದ ಭಾಗಗಳಿಂದ ಗುರುತಿಸಿದೆ. ಹಾಗೆಯೇ ಚಿತ್ರ 2 ರಲ್ಲಿ A ∩ B ಯನ್ನು ಕ್ಷಿತಿಜೀಯ ಗೆರೆಗಳು ತುಂಬಿರುವ ಭಾಗ ತೋರಿಸುತ್ತದೆ.

ಚಿತ್ರ 1

ಚಿತ್ರ 2

ಬೂಲಿಯನ್ ಬೀಜಗಣಿತ

ದತ್ತಗಣ S ನ ಸಮಸ್ತ ಉಪಗಣಗಳ ಸಂಯೋಗ (U) ಮತ್ತು ಛೇದನ (∩) ಪರಿಕರ್ಮಗಳಿಗೆ ಅನುಸಾರವಾಗಿ ಪಾಲಿತವಾಗುವ ಕೆಲವು ನಿಯಮಗಳನ್ನು ಅಮೂರ್ತೀಕರಿಸಿ ಅವುಗಳಿಂದ ದೊರೆಯುವ ಸಂಬಂಧಗಳನ್ನೇ ಆದ್ಯುಕ್ತಿಗಳಾಗಿ (ಪಾಸ್ಟ್ಯುಲೇಟ್ಸ್) ತೆಗೆದುಕೊಂಡು ಅವುಗಳ ಆಧಾರಗಳ ಮೇಲೆ ರಚಿತವಾಗಿರುವ ಗಣಿತ ಶಾಖೆಗೆ ಬೂಲಿಯನ್ ಬೀಜಗಣಿತವೆಂದು ಹೆಸರು. ತರ್ಕಶಾಸ್ತ್ರದಲ್ಲಿ ಬರುವ ವರ್ಗಸಿದ್ಧಾಂತದಲ್ಲಿ (ಥಿಯೊರಿ ಆಫ್ ಕ್ಲಾಸಸ್) ಬೀಜಗಣಿತದ ಸೂತ್ರಗಳನ್ನು ಅನ್ವಯಿಸಲು ಹೊರಟವರಲ್ಲಿ ಮೊದಲಿಗನಾದ ಜಾರ್ಜ್ ಬೂಲ್ ಎಂಬ ಇಂಗ್ಲಿಷ್ ತರ್ಕ ಮತ್ತು ಗಣಿತಶಾಸ್ತ್ರಜ್ಞನ ಹೆಸರಿನಲ್ಲಿ ಈ ಬೀಜಗಣಿತ ಪ್ರಸಿದ್ಧವಾಗಿದೆ. ಬೂಲಿಯನ್ ಬೀಜಗಣಿತವು ಗಣಿತ ಸಿದ್ಧಾಂತವೊಂದೇ ಅಲ್ಲದೆ ಇನ್ನೂ ಅನೇಕ ವಾಸ್ತವಿಕ ಸನ್ನಿವೇಶಗಳಲ್ಲಿ ಅರ್ಥಪೂರಿತವಾಗಿ ಅನ್ವಯವಾಗಿದೆ. S ಒಂದು ವಿಶ್ವಗಣವೂ, P(S) ಇದರ ಘಾತಗಣವೂ ಆಗಿರಲಿ. ಈಗ A, B, C ಗಳು P(S) ಗೆ ಸೇರಿರುವ ಯಾವ ಧಾತುಗಳಾದರೂ ಸಂಯೋಗ ಮತ್ತು ಛೇದನ ಕ್ರಿಯೆಗಳಲ್ಲಿ ಅವು ಮುಂದೆ ಕಾಣಿಸಿರುವ ಸಂಬಂಧಗಳನ್ನು ಏರ್ಪಡಿಸುವುದನ್ನು ಹಿಂದೆಯೇ ನೋಡಿದ್ದೇವೆ.

1. A U B = B U A, A ∩ B = B ∩ A
2. A U ∅ = A, A ∩ S = A
3. A U (B ∩ C) = (A U B) ∩ (A U C), A ∩ (B U C) = (A ∩ B) U (A ∩ C)
4. A U A' = S, A ∩ A' = ∅

ಈಗ ಮೇಲಿನ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಅಮೂರ್ತೀಕರಿಸೋಣ.

B ಒಂದು ಗಣವನ್ನೂ, ∨ ಮತ್ತು ∧ ಎಂಬ ಚಿಹ್ನೆಗಳು B ಯಲ್ಲಿ ವ್ಯಾಖ್ಯಿಸಿರುವ ಎರಡು ದ್ವಿಗುಣ ಪರಿಕರ್ಮಗಳನ್ನೂ ಸೂಚಿಸಲಿ. ಈ ಪರಿಕರ್ಮಗಳು B ಗೆ ಸೇರಿದ ಎಲ್ಲ ಧಾತು a, b, c.... ಗಳಿಗೂ ಮುಂದೆ ಹೇಳಿರುವ ಆದ್ಯುಕ್ತಿಗಳನ್ನು ಪಾಲಿಸುವಂತಿದ್ದರೆ B(v, ∧) ಎಂಬ ವ್ಯವಸ್ಥೆಯನ್ನು (ಸಿಸ್ಟಂ) ಒಂದು ಬೂಲಿಯನ್ ಬೀಜಗಣಿತವೆಂದು ಕರೆಯುತ್ತೇವೆ.^{[೧೫][೧೬]}

1. ವ್ಯತ್ಯಯ ನಿಯಮ

a v b = b v a

a ∧ b = b ∧ a

2. v ಎಂಬ ಪರಿಕರ್ಮಕ್ಕೆ z ಎಂಬ ಒಂದು ಏಕಾಂಶವು, ∧ ಎಂಬುದಕ್ಕೆ u ಎಂಬ ಒಂದು ಏಕಾಂಶವೂ B ಯಲ್ಲಿರುತ್ತವೆ. ಇವು ಪರಸ್ಪರ ಪ್ರತ್ಯೇಕ. ಎಂದರೆ

a v z = a, a ∧ u = a, z ≠ u

3. ಪ್ರತಿಯೊಂದು ಪರಿಕರ್ಮವೂ ಇನ್ನೊಂದರೊಂದಿಗೆ ವಿತರಣ ನಿಯಮವನ್ನು ಅನುಸರಿಸುತ್ತದೆ.

a v (b ∧ c) = (a v b) ∧ (a v c)

a ∧ (b v c) = (a ∧ b) v (a ∧ c)

4. B ಯ ಪ್ರತಿಯೊಂದು ಧಾತು a ಗೂ

a v a' = u ಮತ್ತು a ∧ a' = z ಆಗುವಂತೆ a' ಎಂಬ ಒಂದು ಧಾತು B ಯಲ್ಲಿರುತ್ತದೆ.

ಇಲ್ಲಿ ಹೇಳಿರುವ ಸನ್ನಿವೇಶಗಳು P(S) ನ ಧಾತುಗಳಾದ S ನ ಸಮಸ್ತ ಉಪಗಣಗಳು U ಮತ್ತು ∩ ಪರಿಕರ್ಮಗಳಿಗೆ ಹೇಗೆ ಹೊಂದಿಕೊಂಡಿವೆ ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು. z ಮತ್ತು u ಗಳು ಅನುಕ್ರಮವಾಗಿ ∅ ಮತ್ತು S ಗಳಿಗೆ ಅನ್ವಯವಾಗುತ್ತವೆ. ಹೀಗೆ ಬೂಲಿಯನ್ ಬೀಜಗಣಿತದ ಆದ್ಯುಕ್ತಿಗಳಿಗೆ ಸರಿಹೊಂದುವ ಒಂದು ಮೂರ್ತ ಪ್ರತಿರೂಪ (ಕಾಂಕ್ರೀಟ್ ಮೋಡೆಲ್) ಇರುವುದರಿಂದ ಮೇಲಿನ ಆದ್ಯುಕ್ತಿಗಳ ಸಮೂಹ ಸಂಗತವಾಗಿದೆ.

ಬೂಲಿಯನ್ ಬೀಜಗಣಿತದ ಕೆಲವು ಮುಖ್ಯ ಗುಣಗಳು

ದ್ವೈತ ತತ್ತ್ವ (ಪ್ರಿನ್ಸಿಪಲ್ ಆಫ್ ಡ್ಯೂಆಲಿಟಿ)

ಮೇಲಿನ ಆದ್ಯುಕ್ತಿಗಳಲ್ಲಿ ಉದ್ದಕ್ಕೂ v ಮತ್ತು ∧ ಪರಿಕರ್ಮಗಳನ್ನೂ ಏಕಾಂಶಗಳಾದ z ಮತ್ತು u ಗಳನ್ನೂ ಪರಸ್ಪರವಾಗಿ ವ್ಯತ್ಯಯಿಸಿದರೆ ಪುನಃ ಇವೇ ಆದ್ಯುಕ್ತಿಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಆದ್ದರಿಂದ ಈ ಕೆಳಗಿನ ಪ್ರಮೇಯಗಳು ದೊರೆಯುತ್ತವೆ.

1. ಬೂಲಿಯನ್ ಬೀಜಗಣಿತದ ಯಾವ ಪ್ರಮೇಯದಲ್ಲೇ ಆಗಲಿ v ಮತ್ತು ∧ ಗಳನ್ನೂ z ಮತ್ತು u ಗಳನ್ನೂ ಪರಸ್ಪರ ವ್ಯತ್ಯಯಿಸಿದರೆ ದೊರೆಯುವ ವಾಕ್ಯವೂ ಒಂದು ಸತತವಾದ ಪ್ರಮೇಯ.

2. a v a = a ಮತ್ತು a ∧ a = a ಎಂಬ ವರ್ಗಸಮ (idempotence) ನಿಯಮಗಳನ್ನು ಪ್ರತಿಯೊಂದು ಧಾತುವೂ ಪಾಲಿಸುತ್ತದೆ.

3. a v u = u ಮತ್ತು a ∧ z = z

4. a ∧ (a v b) = a ಮತ್ತು a v (a ∧ b) = a (ವಿಲೀನಕ ನಿಯಮಗಳು-ಅಬ್ಸಾರ್ಪ್ಷನ್ ಲಾಸ್)

5. a v (b v c) = (a v b) v c ಮತ್ತು

a ∧ (b ∧ c) = (a ∧ b) ∧ c (ವಿತರಣ ನಿಯಮಗಳು)

6. ದತ್ತ a ಗೆ ಅನ್ವಯಿಸುವ a' ಏಕೈಕವಾದುದು. ಎಂದರೆ

a v a' = u, a v aⁿ = u ಮತ್ತು

a ∧ a' = z, a ∧ aⁿ = z ಆಗಿದ್ದರೆ ಆಗ

a' = aⁿ

7. ಡಿಮಾರ್ಗನ್‌ನ ನಿಯಮಗಳು:

(a v b)' = a' ∧ b' ಮತ್ತು

(a ∧ b)' = a' v b'

ವ್ಯಾಖ್ಯೆ: a ಮತ್ತು b ಗಳು B ಗೆ ಸೇರಿದ ಧಾತುಗಳಾಗಿದ್ದು a v b = b ಆದಾಗ ಮತ್ತು ಆದಾಗ ಮಾತ್ರ a < b (a ಯು b ಗಿಂತ ಚಿಕ್ಕದು) ಎಂದು ವ್ಯಾಖ್ಯಿಸುತ್ತೇವೆ. ಇದನ್ನು B ಯ ಅನುಕ್ರಮ ಸಂಬಂಧವೆನ್ನುತ್ತೇವೆ. ಇದರ ಸಂಬಂಧದಲ್ಲಿ ಕೆಲವು ಪ್ರಮೇಯಗಳನ್ನು ಮುಂದೆ ಬರೆದಿದೆ.

8. B ಯ ಎಲ್ಲ a ಗಳೂ a<a,

9. a < b ಮತ್ತು b < a ಆಗಿದ್ದರೆ ಆಗ a = b

10. a < b ಮತ್ತು b < c ಆಗಿದ್ದರೆ ಆಗ a < c (ವಾಹಕ ನಿಯಮ)

11. B ಯ ಪ್ರತಿಯೊಂದು a ಗೂ z < a < u

12. a < x ಮತ್ತು b < x ಆಗಿದ್ದರೆ ಆಗ (a v b) < x

ಸಂಬಂಧಗಳು ಮತ್ತು ಉತ್ಪನ್ನಗಳು

ಅನೇಕ ಸಂದರ್ಭಗಳಲ್ಲಿ ಒಂದು ಗಣದ ಕೆಲವು ಧಾತುಗಳೊಂದಿಗೆ, ಅದೇ ಗಣದ ಅಥವಾ ಬೇರೊಂದು ಗಣದ ಕೆಲವು ಧಾತುಗಳು ಯಾವುದೋ ಒಂದು ರೀತಿಯಲ್ಲಿ ಅನ್ವಯಗೊಂಡಿರುವ ಪರಿಸ್ಥಿತಿಗಳು ಉದ್ಭವಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಒಂದು ಶಾಲೆಯ ಎಲ್ಲ ವಿದ್ಯಾರ್ಥಿಗಳ ಗಣ S ಗೂ ಈ ವಿದ್ಯಾರ್ಥಿಗಳ ಪೋಷಕರ ಗಣ T ಗೂ ಮುಂದೆ ಹೇಳಿರುವಂತೆ ಒಂದು ಅನ್ವಯವನ್ನು ಕಲ್ಪಿಸಬಹುದು. ಈ ಶಾಲೆಯಲ್ಲಿ s ಒಬ್ಬ ವಿದ್ಯಾರ್ಥಿಯಾಗಿದ್ದರೆ, ಎಂದರೆ s ∈ S ಆಗಿದ್ದರೆ ಆಗ s ನೊಂದಿಗೆ ಇವನ ಪೋಷಕನನ್ನು ಸೂಚಿಸುವ T ಗಣದಲ್ಲಿರುವ ಒಂದು ಧಾತು t ಯನ್ನು ಹೊಂದಿಸೋಣ. ಹೀಗೆ s ನೊಂದಿಗೆ t ಗಿರುವ ಅನ್ವಯವನ್ನು t=Φ(s) ಎಂಬ ರೂಪದಲ್ಲೋ, ಕ್ರಮಯುಕ್ತ ಧಾತುಯುಗ್ಮವಾಗಿ (s,t) ರೂಪದಲ್ಲೋ ನಿರೂಪಿಸುವುದು ವಾಡಿಕೆ. ಇಲ್ಲಿ S ಗೆ ಸೇರಿದ ಬೇರೆ ಬೇರೆ s₁, s₂ ಗಳಿಗೆ T ಯಲ್ಲಿರುವ ಒಂದೇ t ಅನ್ವಯವಾಗಬಹುದೆಂಬುದನ್ನು ಗಮನಿಸಬೇಕು. ಏಕೆಂದರೆ s₁, s₂ ವಿದ್ಯಾರ್ಥಿಗಳಿಬ್ಬರಿಗೆ ಪೋಷಕ t ಒಬ್ಬರೇ ಇರಬಹುದಲ್ಲವೆ? ಹೀಗೆಯೇ ಎಲ್ಲ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ N ನಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಸಂಖ್ಯೆ n ನೊಂದಿಗೂ ಅದರ ಉತ್ತರಾಂಶ (ಸಕ್ಸೆಸ್ಸರ್) ಎಂದರೆ ಅದರ ಮುಂದಿನ ಸಂಖ್ಯೆ (n+1) ನ್ನು ಅನ್ವಯಿಸಬಹುದು. ಇದನ್ನು (n, n+1) ಎಂಬ ರೂಪದ ಕ್ರಮಯುಕ್ತ ಸಂಖ್ಯಾಯುಗ್ಮಗಳಿಂದ ಸೂಚಿಸಬಹುದು. ಈ ಬಗೆಯ ಮೂರ್ತ ಸನ್ನಿವೇಶಗಳಿಗೆ ಹೊಂದುವ ಗಣಿತ ಆದರ್ಶಗಳಿಗೆ ಸಂಬಂಧಗಳು (ರಿಲೇಷನ್ಸ್) ಮತ್ತು ಚಿತ್ರಣಗಳು (ಮ್ಯಾಪ್ಪಿಂಗ್ಸ್) ಅಥವಾ ಉತ್ಪನ್ನಗಳು (ಫಂಕ್ಷನ್ಸ್) ಎನ್ನುತ್ತೇವೆ.

ಕಾರ್ಟೀಸಿಯನ್ ಗುಣಲಬ್ಧಗಳು (ಕಾರ್ಟೀಸಿಯನ್ ಪ್ರೋಡಕ್ಟ್ಸ್)

S (≠ ∅) ಮತ್ತು T (≠ ∅) ಎರಡು ದತ್ತ ಗಣಗಳಾಗಿರಲಿ. ಈಗ s ಸೇರಿದ S ಮತ್ತು t ಸೇರಿದೆ T ಆಗಿರುವಂತೆ (s, t) ರೂಪದಲ್ಲಿರುವ ಎಲ್ಲ ಕ್ರಮಯುಕ್ತ ಧಾತುಯುಗ್ಮಗಳನ್ನು ನಿರ್ಮಿಸೋಣ. ಇವುಗಳಿಂದಲೇ ಕೂಡಿರುವ ಗಣವನ್ನು S ಮತ್ತು T ಗಳ ಕಾರ್ಟೀಸಿಯನ್ ಗುಣಲಬ್ಧ ಎಂದು ಕರೆಯುತ್ತೇವೆ;^[೧೭] ಹಾಗೂ ಇದನ್ನು S X T ಎಂದು ನಿರೂಪಿಸುತ್ತೇವೆ.

S X T = {(s, t) | ∀ s ∈ S ಮತ್ತು t ∈ T}^{[೧೮][೧೯]}

ಉದಾಹರಣೆ: S = {1, 2, 3, 4} ಮತ್ತು T = {a, b, c}

ಆಗಿದ್ದರೆ ಆಗ S X T = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c), (4, a), (4, b), (4, e)}

ಇದರಲ್ಲಿ 4 X 3 = 12 ಧಾತುಗಳಿವೆ. ಹೀಗೆ S ಮತ್ತು T ಗಳು ಸಾಂತ ಗಣಗಳಾಗಿದ್ದು S ನಲ್ಲಿ m ಧಾತುಗಳೂ, T ಯಲ್ಲಿ n ಧಾತುಗಳೂ ಇದ್ದರೆ ಆಗ S X T ಯಲ್ಲಿ mn ಧಾತುಗಳಿರುತ್ತವೆ.

ಹೀಗೆಯೇ S₁, S₂, ......, S_n ಗಳು n ಅಶೂನ್ಯ ಗಣಗಳಾಗಿದ್ದರೆ ಆಗ {(s₁, s₂, ............., s_n) | s_i ∈ S_i, ∀i = 1, 2, 3..............n} ಎಂಬ ಗಣವನ್ನು S₁, S₂ ........., S_n ಗಳ ಕಾರ್ಟೀಸಿಯನ್ ಗುಣಲಬ್ಧವೆಂದು ಕರೆಯುತ್ತೇವೆ. ಇದನ್ನು S₁ X S₂ X ... X S_n ಎಂದು ನಿರೂಪಿಸುತ್ತೇವೆ. S₁, S₂, ...S_n ಗಳು ಅಶೂನ್ಯ ಗಣಗಳಾಗಿದ್ದರೆ S₁ X S₂ X ... X S_n ಸಹ ಅಶೂನ್ಯ ಗಣ ಎಂಬ ನಿರೂಪಣೆಗೆ ಆಯ್ಕೆಯ ಆದ್ಯುಕ್ತಿ (ಆಕ್ಸಿಯಂ ಆಫ್ ಚಾಯ್ಸ್) ಎಂದು ಹೆಸರು. ಇದನ್ನೂ ಇದರ ಬೇರೊಂದು ರೂಪವಾದ ಜ಼ೋರ್ನ್‌ನ ಉಪಪ್ರಮೇಯವನ್ನೂ ಪ್ರೌಢಗಣಿತದಲ್ಲಿ ಅನೇಕ ಕಡೆ ಬಳಸುತ್ತೇವೆ.

ಸಂಬಂಧಗಳು

S ಮತ್ತು T ಗಳು ಎರಡು ಗಣಗಳಾಗಿದ್ದರೆ SxT ಯ ಪ್ರತಿಯೊಂದು ಉಪಗಣವನ್ನೂ S ನಿಂದ T ಗಿರುವ ಒಂದು ಸಂಬಂಧ (ರಿಲೇಷನ್) ಎಂದು ಕರೆಯುತ್ತೇವೆ.^[೨೦]

ಉದಾಹರಣೆ: S = {1, 2, 3, 4} ಮತ್ತು T = {a, b, c} ಆಗಿದ್ದರೆ ಆಗ R = {(1, b), (1, c), (2, b), (3, b)} ಯು S ನಿಂದ T ಗಿರುವ ಒಂದು ಸಂಬಂಧ. ಈ ಸಂಬಂಧದಲ್ಲಿ S ನಲ್ಲಿರುವ 1 ಕ್ಕೆ T ಯಲ್ಲಿನ b ಮತ್ತು c ಗಳೆರಡೂ ಅನ್ವಯಿಸುತ್ತವೆ. ಆದರೆ S ನಲ್ಲಿರುವ 4 ಕ್ಕೆ T ಯ ಯಾವ ಧಾತುವೂ ಅನ್ವಯವಾಗಿಲ್ಲ. ಹೀಗೆಯೇ T ಯಲ್ಲಿರುವ a ಯು S ನಲ್ಲಿರುವ ಯಾವ ಧಾತುವಿಗೂ ಅನ್ವಯಿಸಿಲ್ಲ.

ಚಿತ್ರಣಗಳು ಅಥವಾ ಉತ್ಪನ್ನಗಳು (ಮ್ಯಾಪ್ಪಿಂಗ್ಸ್ ಆರ್ ಫಂಕ್ಷನ್ಸ್)

S ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತು s ನ್ನೂ ಮೊದಲನೆಯ ಘಟಕವಾಗಿ ಪಡೆದಿರುವ ಎಲ್ಲ (s, t) ಗಳಿಂದ ಏರ್ಪಟ್ಟ S X T ಯ ಒಂದು ಗಣ f ನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ. ಈಗ t₁ = t₂ ಆದಾಗ ಮತ್ತು ಆದಾಗ ಮಾತ್ರ (s, t₁) ಮತ್ತು (s, t₂) ಗಳೆರಡೂ f ನಲ್ಲಿರುವಂತಿದ್ದರೆ f ನ್ನು S ನಿಂದ T ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ಚಿತ್ರಣ ಅಥವಾ ಉತ್ಪನ್ನವೆಂದು ಕರೆಯುತ್ತೇವೆ; ಮತ್ತು f: S→T ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಇದರಿಂದ S ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು s ಗೂ T ಯಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟವಾದ ಧಾತು t ಅನ್ವಯವಾಗಿರುತ್ತದೆ.

ಉದಾಹರಣೆ: X = {1, 2, 3} ಮತ್ತು Y = {D, B, C, A} ಆಗಿರಲಿ. ಈಗ f = {(1, D), (2, C), (3, C)} ಎಂಬುದು X ನಿಂದ Y ಗೆ ಚಿತ್ರಿಸುವ ಒಂದು ಉತ್ಪನ್ನ. ಇಲ್ಲಿ X ನ ಪ್ರತಿಯೊಂದು ಧಾತುವಿಗೂ Y ಯಲ್ಲಿ ಒಂದು ಧಾತು ಸಂವಾದಿಯಾಗಿದೆ. ಈ ಸಂವಾದಿತ್ವವನ್ನು ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದೆ.

ಇದನ್ನು ಸಮೀಕರಣಗಳ ರೂಪದಲ್ಲಿ ಮುಂದೆ ಕೊಟ್ಟಿರುವ ಹಾಗೆ ತೋರಿಸುವುದು ವಾಡಿಕೆ. f(1) = D, f(2) = C, f(3) = C. Y ಯಲ್ಲಿರುವ D ಯು f ಉತ್ಪನ್ನ ಅಥವಾ ಚಿತ್ರಣದಲ್ಲಿ ‌ ನಲ್ಲಿರುವ 1 ರ ಬಿಂಬ; C ಯು 2 ಮತ್ತು 3 ರ ಬಿಂಬ. ಹೀಗೆ ಉತ್ಪನ್ನಗಳಲ್ಲಿ ‌X ನಲ್ಲಿರುವ ಎರಡು ಅಥವಾ ಹೆಚ್ಚು ಧಾತುಗಳಿಗೂ Y ಯಲ್ಲಿ ಒಂದೇ ಬಿಂಬವಿರಬಹುದು. ಆದರೆ Y ಯಲ್ಲಿರುವ B ಯು X ನಲ್ಲಿರುವ ಯಾವ ಧಾತುವಿನೊಂದಿಗೂ ಅನ್ವಯವಾಗುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ Y ಯಲ್ಲಿರುವ ಧಾತುಗಳ f ಬಿಂಬಗಳಿಂದ ಏರ್ಪಡುವ ಗಣ {D, C} ಯು Y ಯನ್ನೆಲ್ಲ ಆಕ್ರಮಿಸುವುದಿಲ್ಲ; ಅದರ ಒಂದು ಸಮುಚಿತ (ಪ್ರಾಪರ್) ಉಪಗಣ ಮಾತ್ರ. ಇದನ್ನು f(X) ಅಥವಾ I_m (f) [ಬಿಂಬ (f)] ಎಂದು ಕರೆಯುತ್ತೇವೆ. X ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತು s ನೊಂದಿಗೆ ಅನ್ವಯವಾಗಿರುವ f(s) ಎಂಬ Y ಯ ಧಾತುವನ್ನು f ಉತ್ಪನ್ನ s ಧಾತುವಿಗೆ Y ಯಲ್ಲಿ ಪಡೆಯುವ ಮೌಲ್ಯವೆಂದು ಹೆಸರು. ಇಲ್ಲಿ X ನ್ನು f ನ (ವ್ಯಾಖ್ಯೆಯ) ಪ್ರಾಂತ (ಡೊಮೇನ್) ಎಂದೂ I_m (f) ನ್ನು f ನ (ಮೌಲ್ಯಗಳ) ವ್ಯಾಪ್ತಿ (ರೇಂಜ್) ಎಂದೂ ಕರೆಯುತ್ತೇವೆ.^[೨೧]

ಮೇಲ್ಚಿತ್ರಣಗಳು, ಒಳಚಿತ್ರಣಗಳು ಮತ್ತು ದ್ವೈಚಿತ್ರಣಗಳು

1. f(S) = T ಆಗಿದ್ದರೆ f ನ್ನು S ನಿಂದ T ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ಮೇಲ್ಚಿತ್ರಣ (ಸರ್ಜೆಕ್ಷನ್) ಎಂದು ಹೇಳುತ್ತೇವೆ.^{[೨೨][೨೩]}

ಉದಾಹರಣೆ : Z = {..., -2, -1, 0, 1, 2...} ಪೂರ್ಣಾಂಕಗಳ ಗಣವೂ, Z' = {0, 1, 4, 9.....} ಎಲ್ಲ ಪೂರ್ಣಾಂಕ ವರ್ಗಸಂಖ್ಯೆಗಳ ಗಣವೂ ಆಗಿದ್ದರೆ Z ನ ಎಲ್ಲ ಧಾತು n ಗಳಿಗೂ f(n) = n² ಎಂದು ವ್ಯಾಖ್ಯಿಸೋಣ. ಈಗ f: Z→Z' ಎಂಬುದು Z ನಿಂದ Z' ಗೆ ವ್ಯಾಖ್ಯಿಸುವ ಒಂದು ಮೇಲ್ಚಿತ್ರಣ.

2. f: S→T ಎಂಬ ಉತ್ಪನ್ನದಲ್ಲಿ s₁≠s₂ ಗಳು S ನ ಧಾತುಗಳಾದಾಗಲೆಲ್ಲ f(s₁)≠f(s₂) ಆಗಿದ್ದರೆ ಎಂದರೆ f(s) = f(s') ಆದಾಗಲೆಲ್ಲ s1=s' ಆಗುವಂತಿದ್ದರೆ f: S→T ಯನ್ನು S ನಿಂದ T ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ಒಳಚಿತ್ರಣ (ಇಂಜೆಕ್ಷನ್) ಎಂದು ಹೇಳುತ್ತೇವೆ.^[೨೪]

ಉದಾಹರಣೆ: N = {0, 1, 2, 3, ...} ಮತ್ತು N' = {1, 2, 3, ...} ಆಗಿದ್ದು f(n) = 2n + 3 ಆಗುವಂತಿದ್ದರೆ f: N→N' ಎಂಬುದು N ನಿಂದ N' ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ಒಳಚಿತ್ರಣ. ಏಕೆಂದರೆ 2n₁+3 = 2n₂+3 ಆಗಿದ್ದರೆ ಆಗ n₁=n₂ ಎಂಬುದು ಸ್ಪಷ್ಟ.

3. f: S→T ಒಂದು ಮೇಲ್ಚಿತ್ರಣವೂ ಒಂದು ಒಳಚಿತ್ರಣವೂ ಆಗಿದ್ದರೆ ಅದನ್ನು S ನಿಂದ T ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ದ್ವೈಚಿತ್ರಣವೆಂದು ಕರೆಯುತ್ತೇವೆ.^[೨೫]

ಉದಾಹರಣೆ: 1. E = {0, 2, 4, 6......} ಮತ್ತು F = {1, 3, 5, 7....} ಆಗಿದ್ದರೆ

ಆಗ f(s) = s + 1, ∀s ∈ E ಎಂಬುದು E ಯಿಂದ F ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ದ್ವೈಚಿತ್ರಣ.

ಈಗ F ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತುವು E ಯಲ್ಲಿರುವ ಒಂದೇ ಒಂದು ಧಾತುವಿನ ಬಿಂಬವಾಗಿರುತ್ತದೆ. ಹೀಗೆ f: E→F ಒಂದು ದ್ವೈಚಿತ್ರಣವಾದರೆ F ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತುವಿಗೂ E ಯಲ್ಲಿರುವ ಒಂದೇ ಒಂದು ಧಾತು ಅನ್ವಯವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ ಈ ಅನ್ವಯ F ನಿಂದ E ಗೆ ಒಂದು ದ್ವೈಚಿತ್ರಣವನ್ನು ನಿರ್ಮಿಸುತ್ತದೆ. ಇದನ್ನು f ನ ವ್ಯಸ್ತವೆನ್ನುತ್ತೇವೆ; ಮತ್ತು f^-1 ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಈಗ f^-1: F→E ಒಂದು ದ್ವೈಚಿತ್ರಣ. ಈ ಉದಾಹರಣೆಯಲ್ಲಿ f^-1: F→E ಚಿತ್ರಣವನ್ನು f^-1(s) = s^-1, ∀s ∈ F ಎಂದು ವ್ಯಾಖ್ಯಿಸಬಹುದು.

4. S ಒಂದು ಗಣವಾಗಿದ್ದರೆ ɛ: S→S ನ್ನು ɛ(s)=s, ∀s ∈ S  ಎಂದು ವ್ಯಾಖ್ಯಿಸಿದರೆ ɛ: S→S ಒಂದು ದ್ವೈಚಿತ್ರಣ. ಇದಕ್ಕೆ S ನ ಸರ್ವಸಮತ್ವ ಚಿತ್ರಣವೆಂದು ಹೆಸರು.^[೨೬]

ಚಿತ್ರಣಗಳ ಸಂಯೋಜನೆ

f: R→S ಮತ್ತು g: S→T ಗಳು ಎರಡು ಚಿತ್ರಣಗಳಾಗಿರಲಿ. ಈಗ r ಸೇರಿದೆ R ಆಗಿದ್ದರೆ f(r) ಎನ್ನುವುದು S ನಲ್ಲಿರುವ ಒಂದು ಧಾತು: ಎಂದರೆ f(r) =s. ಈಗ g(s), T ಯ ಒಂದು ಧಾತು t; ಎಂದರೆ g(s) = t. ಆದರೆ s = f(r). ಆದ್ದರಿಂದ g(f(r)) = ಣ. ಇದನ್ನು ಸಂಕ್ಷೇಪವಾಗಿ (gf) (r) = t ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಹೀಗೆ R ನಲ್ಲಿರುವ ಪ್ರತಿ r ಗೂ T ಯಲ್ಲಿರುವ ಒಂದು ಧಾತುವನ್ನು gf ಅನ್ವಯಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ gf: R→T ಯು R ನಿಂದ T ಗೆ ವ್ಯಾಖ್ಯಿಸಿರುವ ಒಂದು ಚಿತ್ರಣ. ಇದಕ್ಕೆ f ಮತ್ತು g ಗಳ ಸಂಯೋಜನೆ ಎಂದು ಹೆಸರು.

f ಮತ್ತು g ಗಳೆರಡೂ ದ್ವೈಚಿತ್ರಣಗಳಾಗಿದ್ದರೆ fg ಸಹ ಒಂದು ದ್ವೈಚಿತ್ರಣವೇ. ಈಗ f^-1 ಮತ್ತು g^-1 ಗಳು f, g ಗಳ ವ್ಯಸ್ತಗಳಾದರೆ (gf)^-1 = g^-1 f^-1 ಎಂದಾಗುತ್ತದೆ.^[೨೭]

ವ್ಯಸ್ತ ಬಿಂಬಗಳು (ಇನ್ವರ್ಸ್ ಇಮೇಜಸ್)

f: S→T ಒಂದು ಚಿತ್ರಣವಾಗಿರಲಿ. ಈಗ P(T) ಮತ್ತು P(S) ಗಳು T ಮತ್ತು S ನ ಘಾತಗಣಗಳಾದರೆ P(T) ಯಿಂದ P(S) ಗೆ f ನ ಮೂಲಕ ಒಂದು ವ್ಯಸ್ತಚಿತ್ರಣವನ್ನು ಹೀಗೆ ವ್ಯಾಖ್ಯಿಸುತ್ತೇವೆ: B ∈ P(T) ಆಗಿದ್ದರೆ ಆಗ A = {s ∈ S|f(s) ∈ B}. ಈಗ A ಯು P(S) ನಲ್ಲಿರುವ ಒಂದು ನಿರ್ದಿಷ್ಟವಾದ ಧಾತು. ಇದನ್ನು f^-1(B) ಎಂದು ನಿರೂಪಿಸುತ್ತೇವೆ. f^-1 ಎಂಬದು P(T) ಯಿಂದ P(S) ಗೆ ವ್ಯಾಖ್ಯಿಸುವ ಒಂದು ಚಿತ್ರಣ. ಇದನ್ನು f ನ ವ್ಯಸ್ತ ಎಂದು ಕರೆಯುವುದೇ ವಾಡಿಕೆ. f^-1(B) ಯನ್ನು f ಚಿತ್ರಣದಲ್ಲಿ B ಯ ವ್ಯಸ್ತಬಿಂಬವೆಂದು ಕರೆಯುತ್ತೇವೆ.^[೨೮] ವ್ಯಸ್ತಚಿತ್ರಣ ಮತ್ತು ಬಿಂಬಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಕೆಲವು ಪ್ರಮೇಯಗಳನ್ನು ಮುಂದೆ ಬರೆದಿದೆ:

1. B ⊂ T ಆಗಿದ್ದರೆ ಆಗ f(f^-1(B) ⊂ B
2. f: S→T ಒಂದು ಮೇಲ್ಚಿತ್ರಣವಾದರರೆ ಆಗ f(f^-1(B)) = B
3. A ⊂ S ಆಗಿದ್ದರೆ ಆಗ A = f^-1(f(A))
4. f ಒಳಚಿತ್ರಣವಾಗಿದ್ದರೆ ಆಗ A=f^-1(f(A))
5. {B_i} ಎಂಬುದು T ಯ ಉಪಗಣಗಳ ಒಂದು ಸಮೂಹವಾಗಿದ್ದರೆ ಆಗ ${\displaystyle f^{-1}(\bigcup _{i}B_{i})=\bigcup _{i}f^{-1}(B_{i})}$  ಮತ್ತು {B_i) ಸಾಂತ ಸಮೂಹವಾಗಿದ್ದರೆ ಆಗ ${\displaystyle f^{-1}(\bigcap _{i}B_{i})=\bigcap _{i}f^{-1}(B_{i})}$

ಗಣಗಳು ಮತ್ತು ಸಂಖ್ಯಾವ್ಯವಸ್ಥೆ

ಗಣ ಸಿದ್ಧಾಂತದ ತತ್ವಗಳನ್ನು ಸಂಖ್ಯೆಗಳ ವ್ಯಾಖ್ಯೆಗೆ ಮತ್ತು ಸಂಖ್ಯಾವ್ಯವಸ್ಥೆಯ (number system) ರಚನೆಗೆ ಹೇಗೆ ಬಳಸಿಕೊಂಡಿದ್ದಾರೆಂದು ಇನ್ನು ನೋಡೋಣ. ಈ ದಿಶೆಯಲ್ಲಿ ಮೊದಲ ಹೆಜ್ಜೆ ಇಟ್ಟವ ಕ್ಯಾಂಟರ್. ಬಲು ಪರಿಚಿತವಾಗಿರುವ 1, 2, 3....... ಮುಂತಾದ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳನ್ನೂ ಅವುಗಳ ಮೇಲೆ ನಡೆಸಬಹುದಾದ ಸಂಕಲನ ಮತ್ತು ಗುಣಾಕಾರಗಳೆಂಬ ಮೂಲ ಪರಿಕರ್ಮಗಳನ್ನೂ ಗಣಸಿದ್ಧಾಂತದ ಪರಿಕಲ್ಪನೆಗಳ ಮೂಲಕ ಈತ ವ್ಯಾಖ್ಯಿಸಿದ್ದಾನೆ. ಇದರಿಂದ ಗಣಿತಶಾಸ್ತ್ರದ ರಚನೆಗೆ ಸಂಖ್ಯಾಸಿದ್ಧಾಂತಕ್ಕಿಂತಲೂ ಆಳವಾಗಿರುವ ಒಂದು ಭದ್ರವಾದ ತಳಹದಿಯನ್ನು ಕೊಟ್ಟಂತಾಯಿತು. ಇದರ ಸ್ಥೂಲ ವಿವರಣೆಯನ್ನು ಇಲ್ಲಿ ಕೊಟ್ಟಿದೆ.

ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವ

f: S→T ಒಂದು ದ್ವೈಚಿತ್ರಣವಾದರೆ S ನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು s ನೊಂದಿಗೂ T ಯಲ್ಲಿರುವ ಒಂದು ನಿರ್ದಿಷ್ಟವಾದ ಧಾತು t ಸಂವಾದಿಯಾಗಿರುತ್ತದೆ. ಹಾಗೆಯೇ f ನ ವ್ಯಸ್ತವಾದ f^-1: T→S ನಿಂದ T ಯಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಧಾತು t ಯೊಂದಿಗೂ S ನಲ್ಲಿರುವ ಒಂದು ನಿರ್ದಿಷ್ಟವಾದ ಧಾತು s ಸಂವಾದಿಯಾಗಿರುತ್ತದೆ. S ಮತ್ತು T ಗಳಿಗಿರುವ ಇಂಥ ಪರಸ್ಪರ ಸಂಬಂಧಕ್ಕೆ ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವ (ಒನ್-ಒನ್ ಕರೆಸ್ಪಾಂಡೆನ್ಸ್) ಎಂದು ಹೆಸರು.

ಉದಾಹರಣೆ: 1. S = {1, 2, 3, 4, 5, 6, 7} ಎಂಬುದು ಮೊದಲನೆಯ ಏಳು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣಕ್ಕೂ, T = {ಸ, ರಿ, ಗ, ಮ, ಪ, ಧ, ನಿ} ಎಂಬ ಸಪ್ತಸ್ವರಗಳ ಗಣಕ್ಕೂ ಒಂದು ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವನ್ನು ಮುಂದೆ ಸೂಚಿಸಿರುವಂತೆ ಕಲ್ಪಿಸಬಹುದು:

f(1) = ಸ, f(2) = ರಿ, f(3) = ಗ, f(4) = ಮ, f(5) = ಪ, f(6) = ಧ, f(7) = ನಿ. ಇದನ್ನೇ ಸಂಕ್ಷೇಪವಾಗಿ ಹೀಗೆ ತೋರಿಸಬಹುದು:

1↔ಸ, 2↔ರಿ, 3↔ಗ, 4↔ಮ, 5↔ಪ, 6↔ಧ, 7↔ನಿ. ಹೀಗೆಯೇ 1↔ರಿ, 2↔ಗ, 3↔ಮ, 4↔ಪ, 5↔ಧ, 6↔ನಿ, 7↔ಸ ಎಂಬ ಸಂವಾದಿತ್ವವೂ S ಮತ್ತು T ಗಳ ನಡುವೆ ಒಂದು ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವ.

2. N = {1, 2, 3, 4, ......} ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣವೂ, M = {1, 4, 9, 16, ....} ವರ್ಗಸಂಖ್ಯೆಗಳ ಗಣವೂ ಆಗಿದ್ದರೆ ಆಗ f(n) = n², ∀n ∈ N ಎಂಬ ಚಿತ್ರಣ N ಮತ್ತು M ಗಳ ನಡುವೆ ಒಂದು ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವವನ್ನು ರೂಪಿಸುತ್ತದೆ. ಈ ಸಂಬಂಧವನ್ನು

1↔1, 2↔4, 3↔9, 4↔16, ..........n↔n², .......... ಎಂದು ಸಹ ಸೂಚಿಸಬಹುದು.

ವ್ಯಾಖ್ಯೆ: A ಮತ್ತು B ಗಣಗಳ ನಡುವೆ ಒಂದು ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವವನ್ನು ಕಲ್ಪಿಸಬಹುದಾದರೆ ಅವೆರಡನ್ನೂ ಸಮಗಣನಾಸಂಖ್ಯಾ (ಈಕ್ವಿಪೊಲ್ಲೆಂಟ್) ಗಣಗಳೆಂದೂ, ಅವೆರಡಕ್ಕೂ ಒಂದೇ ಗಣನಸಂಖ್ಯೆ (ಕಾರ್ಡಿನಲ್ ನಂಬರ್) ಉಂಟೆಂದೂ ಹೇಳುತ್ತೇವೆ.^{[೨೯][೩೦]} A ಯು B ಗೆ ಸಮಾನವೆಂಬುದನ್ನು A ~ B ಎಂಬುದಾಗಿ ಬರೆಯುತ್ತೇವೆ. A ಯ ಗಣನಸಂಖ್ಯೆಯನ್ನು C(A) ಎಂದು ಸೂಚಿಸೋಣ.

ಹೀಗಾಗಿ ಮೇಲಿನ ಉದಾಹರಣೆಗಳಲ್ಲಿ

1. C(S) = C(T), ಮತ್ತು
2. C(N) = C(M)

ಗಣಗಳ ಗಣನಸಂಖ್ಯೆಗಳ ಮೂಲಕ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳನ್ನು ವ್ಯಾಖ್ಯಿಸುತ್ತೇವೆ. ಒಂಟಿ ಧಾತುವಿರುವ {a}, {b}, {c} ಮುಂತಾದ ಗಣಗಳು ಪರಸ್ಪರ ಸಮಗಣನ ಸಂಖ್ಯಾಗಣಗಳೆಂಬುದು ಸ್ಪಷ್ಟ. ಇವುಗಳ ಗಣನಸಂಖ್ಯೆಯನ್ನು `ಒಂದು' ಎಂಬ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯೆಂದು ವ್ಯಾಖ್ಯಿಸುತ್ತೇವೆ; ಮತ್ತು ಅದನ್ನು 1 ಎಂಬ ಪ್ರತೀಕದಿಂದ ನಿರೂಪಿಸುತ್ತೇವೆ. {a, b} {c, d} ಮುಂತಾದ ಸಮಗಣನಸಂಖ್ಯಾಗಣಗಳ ಗಣನಸಂಖ್ಯೆಯನ್ನು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆ `ಎರಡು' ಎಂದು ಕರೆಯುತ್ತೇವೆ; ಮತ್ತು ಅದನ್ನು 2 ಎಂಬ ಪ್ರತೀಕದಿಂದ ನಿರೂಪಿಸುತ್ತೇವೆ. ಹೀಗೆಯೇ C{a, b, c}= C{p, q, r} = ಮೂರು = 3 ಇತ್ಯಾದಿ. ಮೇಲಿನ ಉದಾಹರಣೆ (1) ರಲ್ಲಿ C(S) = C(T) = 7.

ಗಣನಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಮೂಲಪರಿಕರ್ಮಗಳು

α ಮತ್ತು β ಗಳು ಎರಡು ಗಣನಸಂಖ್ಯೆಗಳೂ, A ಮತ್ತು B ಗಳು ಈ ಗಣನಸಂಖ್ಯೆಗಳನ್ನು ಹೊಂದಿರುವ ಎರಡು ಗಣಗಳೂ ಆಗಿರಲಿ. A ಗೆ ಸಮಗಣನ ಸಂಖ್ಯೆಯಲ್ಲಿರುವ ಎಲ್ಲ ಗಣಗಳ ಗಣನ ಸಂಖ್ಯೆಯೂ ಒಂದೇ ಆಗಿರುವುದರಿಂದ, ಸಾಮಾನ್ಯವಾಗಿ A ಮತ್ತು B ಗಳಿಗೆ ಯಾವ ಸಾಮಾನ್ಯ ಗಣವೂ ಇಲ್ಲದಂತೆ, ಎಂದರೆ A ∩ B = ∅ ಆಗುವಂತೆ ಇವನ್ನು ಆರಿಸಿಕೊಳ್ಳಬಹುದು. ಈಗ A U B ಗಣದ ಗಣನ ಸಂಖ್ಯೆಯನ್ನು α ಮತ್ತು β ಗಳ ಮೊತ್ತವೆಂದು ಕರೆಯುತ್ತೇವೆ, ಮತ್ತು ಇದನ್ನು C(A U B) = α + β = C(A) + C(B) ಎಂದು ಬರೆಯುತ್ತೇವೆ. α ಮತ್ತು β ಗಳಿಂದ ಹೊರಟು α + β ವನ್ನು ಪಡೆಯುವ ಈ ಕ್ರಿಯೆಯನ್ನು ಗಣನಸಂಖ್ಯೆಗಳ ಸಂಕಲನವೆಂದು (sum of cardinality) ಕರೆಯುತ್ತೇವೆ. ಹೀಗೆಯೇ A ಮತ್ತು B ಗಳ ಕಾರ್ಟೀಸಿಯನ್ ಗುಣಲಬ್ಧವಾದ A X B ಗಣದ ಗಣನಸಂಖ್ಯೆಯನ್ನು α ಮತ್ತು β ಗಳ ಗುಣಲಬ್ಧವೆಂದು ಕರೆಯುತ್ತೇವೆ. ಇದನ್ನು α . β ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಎಂದರೆ,

C(A X B) = C(A).C(B) = α.β

α ಮತ್ತು β ಗಳಿಂದ ಹೊರಟು α . β ವನ್ನು ಪಡೆಯುವ ಈ ಕ್ರಿಯೆಗೆ ಗಣನಸಂಖ್ಯೆಗಳ ಗುಣಾಕಾರವೆಂದು (product of cardinality) ಹೆಸರು. ಈ ವ್ಯಾಖ್ಯೆಗಳಿಂದ α ಮತ್ತು β ಗಳು ಗಣನಸಂಖ್ಯೆಗಳಾದರೆ α + β ಮತ್ತು α.β ಗಳೂ ಗಣನಸಂಖ್ಯೆಗಳೇ ಎಂಬುದು ಸ್ಪಷ್ಟ.

ಎಲ್ಲ ಗಣನಸಂಖ್ಯೆಗಳ ಗಣ C ಯಲ್ಲಿ ಸಂಕಲನ ಮತ್ತು ಗುಣಾಕಾರಗಳು ಮುಂದೆ ಕೊಟ್ಟಿರುವ ನಿಯಮಗಳನ್ನು ಪಾಲಿಸುತ್ತವೆ: α, β, γ ಗಳು ಗಣನಸಂಖ್ಯೆಗಳಾಗಿರಲಿ. ಆಗ

1. ಸಹಚರ್ಯ ನಿಯಮ: (α + β) + γ = α + (β + γ); (αβ)γ = α(βγ)
2. ವ್ಯತ್ಯಯ ನಿಯಮ: α + β = β + α; αβ = βα
3. 1.a = a
4. ವಿತರಣ ನಿಯಮ: α.(β + γ) = α.β + α.γ

ಸಾಂತ, ಅನಂತ ಮತ್ತು ಗಣನೀಯ ಗಣಗಳು (ಫೈನೈಟ್, ಇನ್ ಫಿನಿಟ್ ಅಂಡ್ ಎನ್ಯೂಮರೆಬಲ್ ಸೆಟ್ಸ್)

1. A ಒಂದು ಗಣವಾಗಿದ್ದು ಅದರ ಗಣನಸಂಖ್ಯೆ C(A) = n ಒಂದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯಾಗಿದ್ದರೆ A ಯನ್ನು ಸಾಂತಗಣವೆಂದೂ ಹೇಳುತ್ತೇವೆ. ಈಗ A ಯು {1, 2, 3, .............,n} ಗಣಕ್ಕೆ ಸಮಗಣನ ಸಂಖ್ಯಾಗಣವೆಂಬುದನ್ನು ಗಮನಿಸಬೇಕು. ಉದಾಹರಣೆಗೆ T = { ಸ, ರಿ, ಗ, ಮ, ಪ, ಧ, ನಿ} ಎಂಬ ಗಣ {1, 2, 3, .......7} ಎಂಬುದಕ್ಕೆ ಸಮಗಣನ ಸಂಖ್ಯಾಗಣ. ಆದ್ದರಿಂದ T ಸಾಂತ ಗಣ. ಮೇಲಿನ ವ್ಯಾಖ್ಯೆಗೆ ಅನುಗುಣವಾಗಿ ಪ್ರತಿಯೊಂದು ನೈಜ ಸಂಖ್ಯೆ n ಗೂ {1, 2, ........., n} ಗಣ ಸಾಂತ. ಅದರ ಗಣನಸಂಖ್ಯೆ ಅಲ್ಲಿರುವ ಧಾತುಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯೇ ಆಗಿದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು.

2. A ಒಂದು ಗಣವಾಗಿದ್ದು, ಅದರಲ್ಲೇ ಇರುವ ಒಂದು ಸಮುಚಿತ ಉಪಗಣ (proper subset) B ಗೆ A ಯು ಸಮಗಣನ ಸಂಖ್ಯೆಯುಳ್ಳದ್ದಾಗಿದ್ದರೆ ಎಂದರೆ C(A) = C(B) ಆಗುವಂತಿದ್ದರೆ A ಯನ್ನು ಒಂದು ಅನಂತ ಗಣವೆಂದು ವ್ಯಾಖ್ಯಿಸುತ್ತೇವೆ.^[೩೧] ಈ ಸಂದರ್ಭದಲ್ಲಿ C(A) = n ಆಗುವಂತೆ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆ n ಎಂಬುದೂ ದೊರೆಯುವುದಿಲ್ಲ.

ಉದಾಹರಣೆ: 1. N = {1, 2, 3 ......} ಎಲ್ಲ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ

M = {1, 4, 9.......} ಎಲ್ಲ ಪೂರ್ಣಾಂಕ ವರ್ಗಸಂಖ್ಯೆಗಳ ಗಣ

ಆಗಿದ್ದರೆ ಆಗ N ~ M ಎಂದರೆ C(N) = C(M). ಆದರೂ M, N ನ ಒಂದು ಸಮುಚಿತ ಉಪಗಣ ಎನ್ನುವುದು ಸ್ಪಷ್ಟ. ಆದ್ದರಿಂದ N ಅನಂತ. ಅದೇ ರೀತಿ M ಕೂಡ ಅನಂತ. ಏಕೆಂದರೆ C(M) ಒಂದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆ m ಆಗಿದ್ದರೆ C(N) = m ಎಂದರೆ N ಸಾಂತ. ಇದು N ನ ಗುಣವನ್ನು ವಿರೋಧಿಸುತ್ತದೆ.

3. Q ಎಲ್ಲ ಪರಿಮೇಯ ಸಂಖ್ಯೆಗಳ ಗಣವೂ T = {x | -1 ≤ x ≤ 1, x ಪರಿಮೇಯ ಸಂಖ್ಯೆ} ಎಂಬ ಗಣವೂ ಆಗಿರಲಿ. ಈಗ f: T→S ಚಿತ್ರಣವನ್ನು f(0) =0 ಮತ್ತು f(x) = 1/x, ∀x ∈ T , x ≠ 0 ಎಂದು ವ್ಯಾಖ್ಯಿಸಿದರೆ f: T→Q ಒಂದು ದ್ವೈಚಿತ್ರಣವೆಂದು ಸುಲಭವಾಗಿ ತೋರಿಬರುತ್ತದೆ. ಆದ್ದರಿಂದ T ~ Q ಎಂದರೆ C(T) = C(Q). ಆದರೆ ಇಲ್ಲಿ T ಯು Q ನ ಒಂದು ಸಮುಚಿತ ಉಪಗಣ. ಅದ್ದರಿಂದ Q ಅನಂತ ಹಾಗೂ T ಕೂಡ ಅನಂತ.

ಇದೇ ರೀತಿ ಎಲ್ಲ ನೈಜ ಸಂಖ್ಯೆಗಳ ಗಣವನ್ನು ಕೂಡ ಅನಂತವೆಂದು ತೋರಿಸಬಹುದು.

ಸಾಂತಾತೀತ ಸಂಖ್ಯೆಗಳು (ಟ್ರಾನ್ಸ್ ಫೈನೈಟ್ ನಂಬರ್ಸ್)

ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ N = {1, 2, 3...} ಅನಂತವೆಂದು ಹಿಂದೆಯೇ ನೋಡಿದ್ದೇವೆ. ಇದಕ್ಕೆ ಸಮಗಣನ ಸಂಖ್ಯೆಯುಳ್ಳ ಎಲ್ಲ ಗಣಗಳನ್ನೂ ಗಣನೀಯ ಗಣಗಳು ಎಂದು ಕರೆಯುತ್ತೇವೆ. ಎಂದರೆ ಅಂಥ ಗಣದ ಧಾತುಗಳನ್ನು ಒಂದನೆಯದು, ಎರಡನೆಯದು, ಮೂರನೆಯದು, ಎಂದು ಮುಂತಾಗಿ ಎಣಿಸಲು ಸಾಧ್ಯ. ಈ ಪರಿಕಲ್ಪನೆಯನ್ನೇ ಎಣಿಸುವಿಕೆ ಎಂದು ವ್ಯಾಖ್ಯಿಸಬಹುದು. ಇಂಥ ಒಂದು ಗಣದ ಧಾತುಗಳನ್ನು {s₁, s₂, s₃.....} ಎಂದು ಸೂಚಿಸಲು ಸಾಧ್ಯ. ಒಂದು ಗಣನೀಯ ಗಣದ ಧಾತುಗಳನ್ನು ಮೇಲೆ ವಿವರಿಸಿದ ಅನುಕ್ರಮದಲ್ಲಿ {s₁, s₂, s₃.....} ಎಂದು ಜೋಡಿಸಿ ಬರೆದರೆ ಒಂದು ಶ್ರೇಢಿ (ಸೀಕ್ವೆನ್ಸ್) ದೊರೆಯುತ್ತದೆ.

ಎಲ್ಲ ಪರಿಮೇಯ ಸಂಖ್ಯೆಗಳ ಗಣ Q ವನ್ನು ಕೂಡ ಒಂದು ಗಣನೀಯ ಗಣವೆಂದು ಸುಲಭವಾಗಿ ತೋರಿಸಬಹುದು: ಎಂದ ಮೇಲೆ C(Q) = C(N). ಆದರೆ, ಇವು ಸಾಂತಗಣಗಳಲ್ಲ. ಆದ್ದರಿಂದ C(Q) = C(N) = d ಎಂಬುದು ಒಂದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯಲ್ಲ. ಹೀಗೆಯೇ R ಎಂಬುದು ಎಲ್ಲ ನೈಜಸಂಖ್ಯೆಗಳ ಗಣವಾದರೆ C(R) = R ಗಣನಸಂಖ್ಯೆಯೂ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯಲ್ಲ. ಹೀಗೆ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳಲ್ಲದ ಗಣನಸಂಖ್ಯೆಗಳೂ ಇವೆ. ಇಂಥ ಗಣನ ಸಂಖ್ಯೆಗಳಿಗೆ ಸಾಂತಾತೀತ ಸಂಖ್ಯೆಗಳೆಂದು ಹೆಸರು.

Z

Z^o

C(N) = d ಯನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಆಕಾರದಲ್ಲಿರುವ ಅಲೆಫ್ ಎಂಬ ಹೀಬ್ರೂ ಅಕ್ಷರವನ್ನು ಉಪಯೋಗಿಸಿ (ಅಲೆಫ಼್ (ಅಲೆಫ್ ಶೂನ್ಯ -Aleph zero)) ಎಂಬ ಸಂಜ್ಞೆಯಿಂದ ನಿರೂಪಿಸುವದು ವಾಡಿಕೆ. C(R) = c ಅವಿಚ್ಛಿನ್ನತೆಯ ಗಣನ ಸಂಖ್ಯೆ (ಕಾರ್ಡಿನಲ್ ನಂಬರ್ ಆಫ್ ದಿ ಕಂಟಿನ್ಯೂವಂ) ಎಂದು ಹೆಸರು.^[೩೨] ಈಗ R ಎಂಬುದು ಗಣನೀಯ ಗಣವಲ್ಲವೆಂದು ಸುಲಭವಾಗಿ ತೋರಿಸಿಕೊಡಬಹುದು. ಈ ಕಾರಣದಿಂದ d ಯು c ಗಿಂತ ಚಿಕ್ಕದು ಎಂದು ಭಾವಿಸಲಾಗಿದೆ. ಇದನ್ನು d < c ಎಂದು ಬರೆಯುತ್ತೇವೆ.

ಎಲ್ಲ ಏಕಮೌಲ್ಯದ ನೈಜ ಉತ್ಪನ್ನಗಳ (ಸಿಂಗಲ್ ವೇಲ್ಯೂಡ್ ರಿಯಲ್ ಫಂಕ್ಷನ್ಸ್) ಗಣದ ಗಣನಸಂಖ್ಯೆ f, c ಗಿಂತಲೂ ದೊಡ್ಡದು ಎಂದು ಕಂಡುಹಿಡಿಯಲಾಗಿದೆ. ಎಂದರೆ d < c < f ಎಂದಾಯಿತು. c ಗಿಂತ ಚಿಕ್ಕದಾಗಿಯೂ d ಗಿಂತ ದೊಡ್ಡದಾಗಿಯೂ ಇರುವ ಗಣನ ಸಂಖ್ಯೆಯನ್ನು ಪಡೆದಿರುವ ಯಾವುದಾದರೂ ಗಣವಿದೆಯೇ ಎಂಬ ಪ್ರಶ್ನೆಗೆ ಇನ್ನೂ ಉತ್ತರ ದೊರೆತಿಲ್ಲ. ಅಂಥ ಒಂದು ಗಣವಿರಲಾರದು ಎಂಬ ಭಾವನೆಯನ್ನು ಅವಿಚ್ಛಿನ್ನತೆಯ ವಾದ (ಕಂಟಿನ್ಯೂವಂ ಹೈಪಾಥಿಸಿಸ್) ಎಂದು ಕರೆಯುತ್ತೇವೆ. ಇದನ್ನು ಗಣಸಿದ್ಧಾಂತದ ಆಧಾರಗಳಿಂದಲೇ ಸಾಧಿಸಲು ಅಸಾಧ್ಯವೆಂಬುದು ಕೆಲವು ವಿದ್ವಾಂಸರ ಮತ.

ಅನಂತ ಗಣಗಳ ಗಣನಸಂಖ್ಯೆಯನ್ನು ಅನಂತಗಳು (ಇನ್ಫಿನಿಟೀಸ್) ಎಂದು ಕರೆಯುವುದು ವಾಡಿಕೆ. ಹೀಗೆ d, c, f ಗಳು ಅನಂತಗಳು. ಈ ಅನಂತಗಳಲ್ಲೇ ಒಂದು ಸ್ವಾಭಾವಿಕವಾದ ದರ್ಜೆ-ಸಂಬಂಧ (ಆರ್ಡರ್ ರಿಲೇಷನ್) ಇರುವುದು ಗಮನಾರ್ಹ. ಏಕೆಂದರೆ d < c < f ಹೀಗೆ ಒಂದಕ್ಕಿಂತ ಒಂದು ಹೆಚ್ಚಿನ ದರ್ಜೆಯಲ್ಲಿರುವ ಅನಂತಗಳನ್ನು ಅನಂತವಾಗಿ ಪಡೆಯಬಹುದೆಂದೂ ತೋರಿಸಬಹುದು.

ಉಪಸಂಹಾರ

ಗಣಸಿದ್ಧಾಂತದ ಬೆಳವಣಿಗೆಯಿಂದ ಗಣಿತದ ಎಲ್ಲ ಪ್ರಕಾರಗಳಲ್ಲೂ ಬಹು ಮುಖ್ಯವೂ ಗಮನಾರ್ಹವೂ ಆದ ನವೀನ ವಿಧಾನಗಳೂ ಹೊಸ ಹೊಸ ದೃಷ್ಟಿಕೋನಗಳೂ ಮೂಡಿಬಂದುವು; ಹೊಸ ಶಾಖೆಗಳೇ ಬೆಳೆಯತೊಡಗಿದುವು. ಬೀಜಗಣಿತಕ್ಕೂ, ಗಣಿತ ವಿಶ್ಲೇಷಣೆಗೂ ಆಧಾರವಾಗಿರುವ ನೈಸರ್ಗಿಕ ಸಂಖ್ಯಾ ವ್ಯವಸ್ಥೆಯನ್ನು ಗಣಸಿದ್ಧಾಂತದ ಪರಿಕಲ್ಪನೆಗಳಿಂದ ಹೇಗೆ ರಚಿಸಿದ್ದಾರೆಂದು ಈಗ ತಾನೇ ನೋಡಿದ್ದೇವೆ. ಆಧುನಿಕ ಬೀಜಗಣಿತದ ಪ್ರಗತಿ ಗಣಸಿದ್ಧಾಂತದ ಪರಿಕಲ್ಪನೆಗಳನ್ನೂ ವಿಧಾನಗಳನ್ನೂ ಅನುಸರಿಸುತ್ತದೆ. ಒಂದು ಗಣದಲ್ಲಿ ಒಂದು ಅಥವಾ ಇನ್ನೂ ಅಧಿಕ ಸಂಖ್ಯೆಯಲ್ಲಿ ದ್ವಿಗುಣ ಪರಿಕರ್ಮಗಳನ್ನು ವ್ಯಾಖ್ಯಿಸಿ ಅವು ಅನುಸರಿಸಬೇಕಾಗಿರುವ ಕೆಲವು ನಿಯಮಗಳನ್ನು ಆದ್ಯುಕ್ತಿಗಳಾಗಿಟ್ಟುಕೊಂಡು ತರ್ಕಯುಕ್ತವಾದ ವಾದಸರಣಿಯಿಂದ ಸಾಧ್ಯವಾಗುವಷ್ಟು ಪ್ರಮೇಯ ಮತ್ತು ಉಪಪ್ರಮೇಯ ಮುಂತಾದ ಎಲ್ಲ ಫಲಗಳನ್ನೂ ಪಡೆಯುತ್ತ ಹೋಗುವ ಸೃಷ್ಟಿಶೀಲ ಪದ್ಧತಿಯೇ ಆಧುನಿಕ ಬೀಜಗಣಿತದ ಮುಖ್ಯ ಮಾರ್ಗ.

ಜ್ಯಾಮಿತಿಯ ಪ್ರಗತಿಯಲ್ಲಿ ಗಣಸಿದ್ಧಾಂತದ ಕೊಡುಗೆ ಅತ್ಯಂತ ಗಮನಾರ್ಹವಾದ ವಿಷಯ. ಗ್ರೀಕರ ಕಾಲದಲ್ಲಿ ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ವಿವಿಧ ರೇಖಾಕೃತಿಗಳು ವಿಶ್ವದಲ್ಲಿ ಚಲಿಸುವ ಬಿಂದುಗಳ ಪಥಗಳು ಎಂದು ಪರಿಗಣಿಸಲಾಗಿತ್ತು. ಅವುಗಳ ಪರಸ್ಪರ ಸರ್ವಸಮತೆ (ಕಾಂಗ್ರುಯೆನ್ಸ್) ವಿಚಾರವೇ ಇಲ್ಲಿನ ಪ್ರಧಾನ ವಿಷಯವಾಗಿತ್ತು. ಇದಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಆಕೃತಿಗಳ ಗುಣವಿಶೇಷಗಳ ಅಧ್ಯಯನವೇ ಈ ಗಣಿತದ ಮುಖ್ಯ ಗುರಿಯಾಗಿತ್ತು. ಕಾಲಕ್ರಮೇಣ ಎರಡು ಸರ್ವಸಮವಾಗಿರುವ ರೇಖಾಕೃತಿ ಕೊಟ್ಟರೆ ಒಂದನ್ನೊಂದಕ್ಕೆ ಪರಸ್ಪರವಾಗಿ ಪರಿವರ್ತಿಸುವ ಎಲ್ಲ ಚಿತ್ರಣಗಳಿಂದ ಏರ್ಪಡುವ ಗ್ರೂಪುಗಳ ಅಧ್ಯಯನ ಜ್ಯಾಮಿತಿಯ ಪ್ರಧಾನ ವಿಷಯವಾಯಿತು. ಈ ವಿವಿಧ ಗ್ರೂಪುಗಳ ಹೆಸರುಗಳಲ್ಲೇ ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ಜೊತೆಗೆ ಇನ್ನೂ ಅನೇಕ ಪ್ರಕಾರದ ಜ್ಯಾಮಿತಿಗಳು ರೂಪುಗೊಂಡವು. ಈಚೆಗೆ ಜ್ಯಾಮಿತಿಯ ಅಧ್ಯಯನದಲ್ಲಿ ಗಣಸಿದ್ಧಾಂತ ತನ್ನದೇ ಆಧ ಹೊಸ ವಿಧಾನಗಳನ್ನು ರೂಢಿಗೆ ತಂದಿದೆ. ಹೀಗಾಗಿ ಬಲು ಅನಿರ್ದಿಷ್ಟವಾಗಿ ಹೆಸರಿಸಲಾಗಿದ್ದ ವಿಶ್ವ ಎಂಬುದನ್ನು ಒಂದು ದತ್ತ ವಿಶ್ವಗಣವೆಂದು ಭಾವಿಸಲಾಯಿತು. ಇದರ ಧಾತುಗಳನ್ನು ಬಿಂದುಗಳೆಂದು ಕರೆದರು. ಇದರಲ್ಲಿನ ಒಂದು ಬಗೆಯ ಸಮುಚಿತ ಉಪಗಣಗಳನ್ನು (ಸರಳ) ರೇಖೆಗಳೆಂದೂ ಇನ್ನೊಂದು ಬಗೆಯ ಸಮುಚಿತ ಉಪಗಣಗಳನ್ನು ಸಮತಲಗಳೆಂದು ಕರೆಯಲಾಯಿತು. ವಿಶಿಷ್ಟ ಗುಣಗಳನ್ನು ಹೊಂದಿರುವ ಬೇರೆ ಬೇರೆ ಸಮುಚಿತ ಉಪಗಣಗಳನ್ನು ರೇಖಾಕೃತಿಗಳು ಎಂದು ವ್ಯಾಖ್ಯಿಸಲಾಯಿತು. ಇಲ್ಲಿನ ಬಿಂದು, ರೇಖೆ, ಮತ್ತು ಸಮತಲಗಳಿಗೆ ಇರಬಯಸಲಾದ ಪರಸ್ಪರ ಸಂಬಂಧಗಳನ್ನು ಆದ್ಯುಕ್ತಿಗಳೆಂದು ಕರೆದು ಅವುಗಳ ಮೂಲಕ ತಾರ್ಕಿಕವಾದ ವಾದಸರಣಿಯಿಂದ ದೊರೆಯುವ ಪ್ರಮೇಯಗಳ ವ್ಯವಸ್ಥೆಯನ್ನೇ ಒಂದು ಜ್ಯಾಮಿತಿ ಎಂದು ಹೇಳಲಾಯಿತು. ಮೂಲಭಾವನೆಗಳಲ್ಲಿ ಸೂಕ್ತವಾದ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡುತ್ತ ಹೋದರೆ ಬೇರೆ ಬೇರೆ ಜ್ಯಾಮಿತಿಗಳು ದೊರೆಯುತ್ತವೆ. ಇದರಿಂದ ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ಜೊತೆಗೆ ಅಯೂಕ್ಲಿಡೀಯ, ವಿಕ್ಷೇಪ, ಅಫೈನ್, ಸರ್ವಸಮತೆ ಮುಂತಾದ ಅನೇಕ ಬಗೆಯ ಜ್ಯಾಮಿತಿಗಳು ಮೂರ್ತಿವೆತ್ತುವು. ಟಾಪಾಲಜಿ ಎಂಬ ಒಂದು ನವೀನ ಪ್ರಕಾರದ ಗಣಿತ ಶಾಖೆ ಬೆಳೆಯಿತು. ಈ ಶಾಖೆಯಲ್ಲಿ ಬೀಜಗಣಿತ, ಗಣಿತ ವಿಶ್ಲೇಷಣೆ ಹಾಗೂ ಜ್ಯಾಮಿತಿಗಳ ಸಂಯೋಗವನ್ನು ಕಾಣಬಹುದು.

ಹೀಗೆ ಗಣಸಿದ್ಧಾಂತದ ಪರಿಕಲ್ಪನೆಗಳು, ವಿಧಾನಗಳು ಮತ್ತು ಪರಿಭಾಷೆ ಗಣಿತದ ಎಲ್ಲ ಶಾಖೆಗಳಿಗೂ ಒಂದು ಸಾಮಾನ್ಯ ಭಾಷೆ ಮತ್ತು ಅಧ್ಯಯನ ಕ್ರಮವನ್ನು ಅಳವಡಿಸಿಕೊಟ್ಟಿವೆ.

ಉಲ್ಲೇಖಗಳು

1. "Introduction to Sets". www.mathsisfun.com. Retrieved 2020-08-20.
2. "AxiomaticSetTheory". www.cs.yale.edu. Retrieved 2024-08-20.
3. "Naive Set Theory". sites.pitt.edu. Retrieved 2024-08-20.
4. Stoll, Robert R. Set Theory and Logic. San Francisco, CA: Dover Publications. ISBN 978-0-486-63829-4.
5. Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (2002-01-01). Basic Set Theory (in ಇಂಗ್ಲಿಷ್). American Mathematical Soc. ISBN 9780821827314.
6. "Stats: Probability Rules". People.richland.edu. Retrieved 2012-05-08.
7. "Intersection of Sets". web.mnstate.edu. Archived from the original on 2020-08-04. Retrieved 2020-09-04.
8. Halmos, P. R. (1960), Naive Set Theory, Undergraduate Texts in Mathematics, Springer, p. 15, ISBN 9780387900926.
9. "Complement and Set Difference". web.mnstate.edu. Retrieved 2020-09-04.
10. Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2016). Introduction to Logic. doi:10.4324/9781315510897. ISBN 9781315510880.
11. Hurley, Patrick J. (2015), A Concise Introduction to Logic (12th ed.), Cengage Learning, ISBN 978-1-285-19654-1
12. Moore, Brooke Noel (2012). Critical thinking. Richard Parker (10th ed.). New York: McGraw-Hill. ISBN 978-0-07-803828-0. OCLC 689858599.
13. Taylor, Courtney (March 31, 2019). "What Is Symmetric Difference in Math?". ThoughtCo (in ಇಂಗ್ಲಿಷ್). Retrieved 2020-09-05.
14. Weisstein
15. O'Regan, Gerard (2008). A brief history of computing. Springer. p. 33. ISBN 978-1-84800-083-4.
16. "Elements of Boolean Algebra". www.ee.surrey.ac.uk. Archived from the original on 2020-07-21. Retrieved 2020-09-02.
17. Weisstein, Eric W., "Cartesian Product", MathWorld.
18. Warner, S. (1990). Modern Algebra. Dover Publications. p. 6.
19. Nykamp, Duane. "Cartesian product definition". Math Insight. Retrieved September 5, 2020.
20. Codd, Edgar Frank (June 1970). "A Relational Model of Data for Large Shared Data Banks" (PDF). Communications of the ACM. 13 (6): 377–387. doi:10.1145/362384.362685. S2CID 207549016. Archived (PDF) from the original on 2004-09-08. Retrieved 2020-04-29.
21. "Mapping". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
22. Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2008). The Princeton Companion to Mathematics (in ಇಂಗ್ಲಿಷ್). Princeton, New Jersey: Princeton University Press. p. 11. doi:10.1515/9781400830398. ISBN 978-0-691-11880-2. JSTOR j.ctt7sd01. LCCN 2008020450. MR 2467561. OCLC 227205932. OL 19327100M. Zbl 1242.00016.
23. Ivanova, O.A. (2001) [1994]. "Surjection". Encyclopedia of Mathematics. EMS Press.
24. Ivanova, O.A. (2001) [1994]. "Injection". Encyclopedia of Mathematics. EMS Press.
25. Ivanova, O.A. (2001) [1994]. "Bijection". Encyclopedia of Mathematics. EMS Press.
26. Knapp, Anthony W. (2006), Basic algebra, Springer, ISBN 978-0-8176-3248-9
27. Rodgers, Nancy (2000). Learning to Reason: An Introduction to Logic, Sets, and Relations. John Wiley & Sons. pp. 359–362. ISBN 978-0-471-37122-9.
28. Dolecki & Mynard 2016, pp. 4–5.
29. Suppes, Patrick (1972) [originally published by D. van Nostrand Company in 1960]. Axiomatic Set Theory. Dover. ISBN 0486616304.
30. Enderton, Herbert (1977). Elements of Set Theory. Academic Press Inc. ISBN 0-12-238440-7.
31. Boolos, George (1998). Logic, Logic, and Logic (illustrated ed.). Harvard University Press. p. 262. ISBN 978-0-674-53766-8.
32. "Transfinite number | mathematics". Encyclopedia Britannica (in ಇಂಗ್ಲಿಷ್). Retrieved 2020-08-12.

ಗ್ರಂಥಸೂಚಿ

• Weisstein, Eric W. "Power Set". mathworld.wolfram.com (in ಇಂಗ್ಲಿಷ್). Archived from the original on 2023-04-06. Retrieved 2020-09-05.
• Dolecki, Szymon; Mynard, Frederic (2016). Convergence Foundations Of Topology. New Jersey: World Scientific Publishing Company. ISBN 978-981-4571-52-4. OCLC 945169917.

ಹೊರಗಿನ ಕೊಂಡಿಗಳು

• Daniel Cunningham, Set Theory article in the Internet Encyclopedia of Philosophy.
• Jose Ferreiros, "The Early Development of Set Theory" article in the [Stanford Encyclopedia of Philosophy].
• Foreman, Matthew, Akihiro Kanamori, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
• "Axiomatic set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Schoenflies, Arthur (1898). Mengenlehre in Klein's encyclopedia.
• Online books, and library resources in your library and in other libraries about set theory
• Rudin, Walter B. (April 6, 1990). "Set Theory: An Offspring of Analysis". Marden Lecture in Mathematics. University of Wisconsin-Milwaukee. Archived from the original on 2021-10-31 – via YouTube.