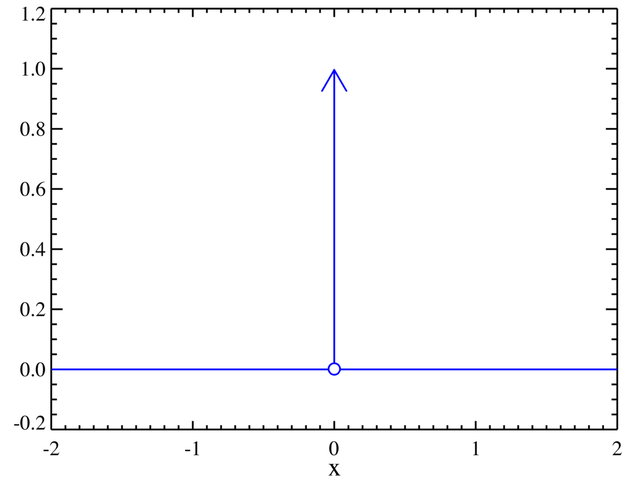
数学 におけるディラック のデルタ関数 （ デルタかんすう 、（ 英 : delta function ） 、または制御工学 におけるインパルス関数 （ インパルスかんすう 、（ 英 : impulse function ） とは、任意の実連続関数
f
:
R
→
R
{\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }
∫
−
∞
∞
f
(
x
)
δ
(
x
)
d
x
=
f
(
0
)
{\displaystyle \int _{-\infty }^{\infty }f(x)\delta (x)\,dx=f(0)}
を満たす実数値シュワルツ超関数 δ クロネッカーのデルタ
∑
i
=
−
∞
+
∞
f
i
δ
i
,
j
=
f
j
{\displaystyle \sum _{i=-\infty }^{+\infty }f_{i}\delta _{i,j}=f_{j}}
の自然な拡張になっている。
ディラックのデルタ関数はデルタ超関数 （英 : delta distribution ）あるいは単にディラックデルタ（英 : Dirac's delta ）とも呼ばれる。これを最初に定義して量子力学の定式化に用いた物理学者ポール・ディラック に因み、この名称が付いている。デルタ関数は古典的な意味での関数ではないシュワルツ超関数（英 : distribution ）の最初の例になっている。
ディラックのデルタの「関数」としての性質は、形式的に次のように述べることができる。まず、f (x )1 をとる関数をとり、デルタ関数をデルタ関数自身と f (x ) = 1
∫
−
∞
∞
δ
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }\delta (x)dx=1}
である。一方、積分値が f の x = 0
δ
(
x
)
=
0
(
x
≠
0
)
{\displaystyle \delta (x)=0\quad (x\neq 0)}
でなければならないが、その上で積分値が 0 でない有限の値をとるためには
δ
(
0
)
=
∞
{\displaystyle \delta (0)=\infty }
が満たされなければならない。
上記のように特徴付けられるデルタ関数 δ x )δ x )x = 0x = 0x ≠ 0δ x ) = 0x ≠ 0δ x ) = 00 の値をとる関数であり、他の関数と掛けて積分しても 0 以外の値をとることはない。点 x = 0積分 が、通常の関数の（広義）リーマン積分 やルベーグ積分 として理解されるならば、このような関数の積分は恒等的に 0 に等しい関数を積分するのと同じであり積分値は 0 になる。したがって、このような条件を満たすような通常の関数は存在しない。
しかし、通常の意味ではまったく関数ではないデルタ関数は、適当な枠組みの下では意味を持ち、例えばデルタ分布はヘヴィサイドの階段関数 の弱微分 （超関数 の意味での微分）を与えている。
デルタ関数は実軸上滑らか で有界 な関数の空間
C
b
∞
(
R
)
{\displaystyle C_{b}^{\infty }(\mathbb {R} )}
汎関数 になっているが、
C
b
∞
(
R
)
{\displaystyle C_{b}^{\infty }(\mathbb {R} )}
双対空間 の中でデルタ関数に弱収束するような関数の族 φ t
∫
−
∞
∞
f
(
x
)
φ
t
(
x
)
d
x
→
f
(
0
)
(
t
→
0
)
{\displaystyle \int _{-\infty }^{\infty }f(x)\varphi _{t}(x)dx\rightarrow f(0)\quad (t\rightarrow 0)}
が任意の
f
∈
C
b
∞
(
R
)
{\displaystyle f\in C_{b}^{\infty }(\mathbb {R} )}
φ t
中心 μ 分散 σ 2 正規分布 の密度関数
ϕ
μ
,
σ
(
x
)
=
1
2
π
σ
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
{\displaystyle \phi _{\mu ,\sigma }(x)={\frac {1}{{\sqrt {2\pi }}\,\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}
は、デルタ関数の満たすべき性質
∫
−
∞
∞
ϕ
μ
,
σ
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }\phi _{\mu ,\sigma }(x)\,dx=1}
を満たす。さらに、μ σ → 0x = 0φ σ x ) → 0 (x ≠ 0)φ σ → +∞ σ → 0φ σ
lim
σ
→
0
1
2
π
σ
exp
(
−
x
2
2
σ
2
)
=
δ
(
x
)
{\displaystyle \lim _{\sigma \to 0}{\frac {1}{{\sqrt {2\pi }}\,\sigma }}\exp \!\left(-{\frac {x^{2}}{2\sigma ^{2}}}\right)=\delta (x)}
と表現される。デルタ関数の表現に正規分布を用いたが、このことから、デルタ関数は正規分布の一種であると考えることが可能である。デルタ関数は、特殊な確率分布 の表現に有用である。
Sinc関数 から変数変換とスケーリングによって得られる関数族
ϕ
k
(
x
)
=
sin
k
x
π
x
(
k
∈
R
)
{\displaystyle \phi _{k}(x)={\frac {\sin kx}{\pi x}}\quad (k\in \mathbb {R} )}
は、デルタ関数の満たすべき条件
∫
−
∞
∞
ϕ
k
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }\phi _{k}(x)\,dx=1}
を満たす。ただし、これは左辺を広義積分
lim
a
→
∞
∫
−
a
a
{\displaystyle \lim _{a\rightarrow \infty }\int _{-a}^{a}}
k → ∞ 各点収束 しないが、任意のコンパクト台 の滑らかな関数 f に対して
lim
k
→
∞
∫
−
∞
∞
f
(
x
)
ϕ
k
(
x
)
d
x
=
f
(
0
)
{\displaystyle \lim _{k\to \infty }\int _{-\infty }^{\infty }f(x)\,\phi _{k}(x)\,dx=f(0)}
が成り立っている。これも弱収束の意味でデルタ関数を近似していると考えられ、
lim
k
→
∞
sin
k
x
π
x
=
δ
(
x
)
{\displaystyle \lim _{k\to \infty }{\frac {\sin kx}{\pi x}}=\delta (x)}
と表現される。
Sinc関数による近似の形をオイラーの公式 を用いて変形すれば
ϕ
k
(
x
)
=
sin
k
x
π
x
=
1
2
π
i
x
[
e
i
k
x
−
e
−
i
k
x
]
=
1
2
π
∫
−
k
k
e
i
k
′
x
d
k
′
{\displaystyle \phi _{k}(x)={\frac {\sin kx}{\pi x}}={\frac {1}{2\pi ix}}\left[e^{ikx}-e^{-ikx}\right]={\frac {1}{2\pi }}\int _{-k}^{k}e^{ik'x}dk'}
であり、フーリエ変換 における基本的な関係式
δ
(
x
)
=
1
2
π
∫
−
∞
∞
e
i
k
x
d
k
{\displaystyle \delta (x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{ikx}dk}
が得られる。この表式は量子場の理論で非常によく利用される[1]
f
^
(
k
)
=
F
[
f
]
=
∫
f
(
x
)
e
−
i
k
x
d
x
{\displaystyle {\hat {f}}(k)={\mathcal {F}}[f]=\int f(x)\,e^{-ikx}dx}
f
(
x
)
=
F
−
1
[
f
^
]
=
1
2
π
∫
f
^
(
k
)
e
i
k
x
d
k
{\displaystyle f(x)={\mathcal {F}}^{-1}[{\hat {f}}]={\frac {1}{2\pi }}\int {\hat {f}}(k)\,e^{ikx}dk}
は、以下の関係式により正当化される。
F
−
1
∘
F
[
f
]
=
1
2
π
∫
[
∫
f
(
y
)
e
−
i
k
y
d
y
]
e
i
k
x
d
k
=
∫
f
(
y
)
[
1
2
π
∫
e
i
k
(
x
−
y
)
d
k
]
d
y
=
∫
f
(
y
)
δ
(
x
−
y
)
d
y
=
f
(
x
)
{\displaystyle {\mathcal {F}}^{-1}\circ {\mathcal {F}}[f]={\frac {1}{2\pi }}\int {\bigg [}\int f(y)\,e^{-iky}dy{\bigg ]}e^{ikx}dk=\int f(y){\bigg [}{\frac {1}{2\pi }}\int e^{ik(x-y)}dk{\bigg ]}dy=\int f(y)\,\delta (x-y)\,dy=f(x)}
佐藤超関数 の流儀では、ディラックのデルタ関数は複素領域から実軸への抽象的境界値
δ
(
x
)
:=
−
1
2
π
i
(
1
x
+
i
0
−
1
x
−
i
0
)
{\displaystyle \delta (x):={\frac {-1}{2\pi i}}\left({\frac {1}{x+i0}}-{\frac {1}{x-i0}}\right)}
と定義される。ここで抽象的境界値とは正則関数のある種の同値類を表すが、直感的には x ≠ 0
−
1
2
π
i
(
1
x
+
i
0
−
1
x
−
i
0
)
=
−
1
2
π
i
(
1
x
−
1
x
)
=
0
{\displaystyle {\frac {-1}{2\pi i}}\left({\frac {1}{x+i0}}-{\frac {1}{x-i0}}\right)={\frac {-1}{2\pi i}}\left({\frac {1}{x}}-{\frac {1}{x}}\right)=0}
である。また、デルタ関数の最も重要な性質である
∫
δ
(
x
)
f
(
x
)
d
x
=
f
(
0
)
{\displaystyle \int \delta (x)f(x)\,dx=f(0)}
は、複素解析学のコーシーの積分公式 から導かれる。厳密な定義には層係数のコホモロジー 論を必要とするが、1 変数の場合は比較的容易に理論展開できる。
ディラック関数は以下のようにして定まるディラック測度 英 : Dirac measure ）δ 0 ボレル部分集合 A に対して、A が 0 を含む場合 δ 0 (A ) = 1δ 0 (A ) = 0δ 0 σ 測度 に関する有界ボレル関数 の積分は
∫
f
(
x
)
d
δ
0
(
x
)
=
f
(
0
)
{\displaystyle \int f(x)d\delta _{0}(x)=f(0)}
であり、形式的に dδ 0 (x ) = δ x )dx
ミクシンスキーの演算子法 に従い、R ≥ 0∞ )C = C ([0, ∞ ); C )畳み込み
(
f
∗
g
)
(
x
)
:=
∫
0
x
f
(
x
−
ξ
)
g
(
ξ
)
d
ξ
{\displaystyle (f*g)(x):=\int _{0}^{x}f(x-\xi )g(\xi )\,d\xi }
に関して零因子 を持たないというティッチマーシュの定理 （英語版 ） 単位元 を持たない可換 な）整域 としての C の商体 M を構築する M はティッチマーシュ・ミクシンスキー代数 や、ミクシンスキー演算子 （ヘヴィサイド演算子、— 超関数）の体などと呼ばれる。M には C にはなかった乗法の単位元 δ δ (x )}δ x )
実際 δ 1 に対応する積分作用素 l = {1} ∈ C ⊂ M lδ = δ ll x に対して
∫
0
x
δ
(
ξ
)
d
ξ
=
1
{\displaystyle \int _{0}^{x}\delta (\xi )\,d\xi =1}
を満たさなければならない（もし δ R ≥ 0x = 00 となるから、これを C の中だけで考えることはできない）。再び形式的な議論だが、この被積分関数を δ x )[0, x ] の指示関数 との値ごとの積と見なすことで、無限区間でのデルタ関数の性質が満たされると考えることができる。一方で、十分小さな ε > 0
∫
ε
x
δ
(
ξ
)
d
ξ
=
∫
0
x
δ
(
ξ
)
d
ξ
−
∫
0
ε
δ
(
ξ
)
d
ξ
=
0
{\displaystyle \int _{\varepsilon }^{x}\delta (\xi )\,d\xi =\int _{0}^{x}\delta (\xi )\,d\xi -\int _{0}^{\varepsilon }\delta (\xi )\,d\xi =0}
だから、x ≠ 0δ x ) = 0
a
>
0
{\displaystyle a>0}
[1]
x
δ
(
x
)
=
0
δ
(
a
x
)
=
|
a
|
−
1
δ
(
x
)
δ
(
x
2
−
a
2
)
=
(
1
/
2
a
)
[
δ
(
x
−
a
)
+
δ
(
x
+
a
)
]
{\displaystyle {\begin{aligned}x\delta (x)&=0\\\delta (ax)&=|a|^{-1}\delta (x)\\\delta (x^{2}-a^{2})&=(1/2a)[\delta (x-a)+\delta (x+a)]\\\end{aligned}}}
n δ (n ) (x )[2]
x
m
δ
(
n
)
(
x
)
=
{
0
,
(
m
>
n
)
(
−
1
)
m
m
!
δ
(
x
)
,
(
m
=
n
)
(
−
1
)
m
n
!
(
n
−
m
)
!
δ
(
n
−
m
)
(
x
)
.
(
m
<
n
)
{\displaystyle x^{m}\delta ^{(n)}(x)={\begin{cases}0,&(m>n)\\(-1)^{m}\ m!\ \delta (x),&(m=n)\\(-1)^{m}{\dfrac {n!}{(n-m)!}}\delta ^{(n-m)}(x).&(m<n)\end{cases}}}
ここで n,m
x
δ
′
(
x
)
=
−
δ
(
x
)
{\displaystyle x\delta '(x)=-\delta (x)}
であるが、xf (x ) = − δ x )f (x )α
f
(
x
)
=
δ
′
(
x
)
+
α
δ
(
x
)
{\displaystyle f(x)=\delta '(x)+\alpha \delta (x)}
である[2]
Weisstein, Eric W. "Delta Function" . mathworld.wolfram.com (英語). Francois Treves (2006). Topological Vector Spaces, Distributions and Kernels . Dover Publications 砂川重信 『量子力学』岩波書店 、1991年、30頁。ISBN 4-00-006139-9 。 
![{\displaystyle \phi _{k}(x)={\frac {\sin kx}{\pi x}}={\frac {1}{2\pi ix}}\left[e^{ikx}-e^{-ikx}\right]={\frac {1}{2\pi }}\int _{-k}^{k}e^{ik'x}dk'}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8ed419c401568f593fd01e6c346a0882bdfb7090)
![{\displaystyle {\hat {f}}(k)={\mathcal {F}}[f]=\int f(x)\,e^{-ikx}dx}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e8ec491569c34916c0980e4837cea562b048f61d)
![{\displaystyle f(x)={\mathcal {F}}^{-1}[{\hat {f}}]={\frac {1}{2\pi }}\int {\hat {f}}(k)\,e^{ikx}dk}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6c36e5ca28519cfa706bf67058511bfc1c2a1945)
![{\displaystyle {\mathcal {F}}^{-1}\circ {\mathcal {F}}[f]={\frac {1}{2\pi }}\int {\bigg [}\int f(y)\,e^{-iky}dy{\bigg ]}e^{ikx}dk=\int f(y){\bigg [}{\frac {1}{2\pi }}\int e^{ik(x-y)}dk{\bigg ]}dy=\int f(y)\,\delta (x-y)\,dy=f(x)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0cbf0e522c447afc061535619583fadbc76a2a12)
![{\displaystyle {\begin{aligned}x\delta (x)&=0\\\delta (ax)&=|a|^{-1}\delta (x)\\\delta (x^{2}-a^{2})&=(1/2a)[\delta (x-a)+\delta (x+a)]\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a438deeba3d6c54c1eaa2920f648bceccf3197ab)
