調和共役 (幾何学)

「共役調和関数」とは異なります。

射影幾何学において、調和共役（ちょうわきょうやく、英語: harmonic conjugate）は、実射影直線における以下の点の関係のことである^{[1][2][3][4][5]}。

同一直線上にある三点 A, B, CについてLをその直線上にない点、M, NをそれぞれあるCを通る直線とLA, LBの交点とする。またANとBMの交点をKとする。LKとABの交点DをCのA,Bに対する調和共役点という^[6][7][8][9]。

DはA,Bに対するCの調和共役
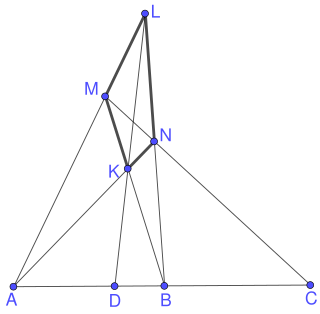
A, D, B, C は調和点列
KLMNは完全四辺形

Dは複比の不変性やデザルグの定理により、点Lや直線MNの取り方に依らない。

またこのときの複比については (A, B; C, D) = −1が成り立つ。

平面幾何学では{P,Q}調和共役（{P,Q}-harmonic conjugate）と書かれることもある^[10]。

複比の基準

A, D, B, Cは調和点列（Harmonic range）または調和列点と呼ばれている^{[11][12][13][14][15][16][17]}。ABに対するDの内分比とCの外分比は常に等しい。つまり以下が成り立つ。$${\displaystyle {\overline {AC}}:{\overline {BC}}={\overline {AD}}:{\overline {DB}}\,.}$$線分比について符号付き距離を導入すると複比は以下の式で表される。

${\displaystyle (A,B;C,D)={\frac {\overline {AC}}{\overline {AD}}}\left/{\frac {\overline {BC}}{-{\overline {DB}}}}\right.,}$

調和点列の複比は常に-1である。

${\displaystyle (A,B;C,D)={\frac {\overline {AC}}{\overline {AD}}}\times {\frac {\overline {BD}}{\overline {BC}}}=-1.}$

複比を取る4点の選びは6通りあり、選び方によって複比の値は変わってしまう。しかし、調和点列の場合、{−1, 1/2, 2}のいずれかとなる。これらは調和比（harmonic cross-ratio）と呼ばれる^{[18][19][20][21]}。

実数直線状の点a, bについて点xの分割比（division ratio）は以下の式で表される^[22][23]。$${\displaystyle t(x)={\frac {x-a}{x-b}}.}$$a < x < bならば、t(x)は負の値を取る。逆にa, bの外であれば正の値を取る。複比は分割比を用いて${\displaystyle (c,d;a,b)={\tfrac {t(c)}{t(d)}}}$ と書くことができる。t(c) + t(d) = 0ならば、cとdはa,bに対する調和共役である。

調和共役の関係にある2つの点との距離が、調和点列の分比である点の軌跡はアポロニウスの円と呼ばれる。

中点の調和共役

中点と無限遠点

aとbの中点xに対しての分割比は-1である。$${\displaystyle t(x)={\frac {x-a}{x-b}}=-1.}$$複比の基準によれば、中点xの調和共役点yはt(y) = 1を満たさなければならない。しかし無限の概念を使わねば、yを定義することができない。$${\displaystyle \lim _{y\to \infty }t(y)=1,}$$中点xの調和共役点は実数直線上の無限遠点として定義される。

完全四角形

調和共役と完全四辺形（英語版）KLMNは深い関係にある。完全四角形の調和共役による表現はH. S. M.コクセターによって提唱された。

どの3点も共線でない4点A,B,C,Dを結んでできる6つの直線のからできる図形を完全四角形または完全四辺形という^[24]。

最初に調和共役を用いたカール・フォン・シュタウトは著作「Geometrie der Lage」の中で、調和共役を初等幾何学の概念から射影幾何学の概念へ発展させた^[25]。

P₁ = A, P₂ = S, P₃ = B, P₄ = Q, D = M

ジョン・ウェスレー・ヤングによれば、完全四角形によって中点を定義することができる。

2直線 AQ, AS についてそれぞれ平行な直線,BS, BQ を描く。 AQ, SB の交点は無限遠点R、AS, QBの交点無限遠点Pである。完全四角形PQRS の対角線は直線ABと、AB上の無限遠点Mである。平行四辺形の対角線の交点は対角線を二等分することより、 Mの調和共役点はABの中点である^[26]。

円錐曲線

→詳細は「極と極線」を参照

円錐曲線CとC上にないPについて、Pを通る直線とCの交点をそれぞれA,Bとする。直線が動くとき、 PのA,Bに対する調和共役点は、ある直線上を動く。この時Pを極（pole）、調和共役点の動く直線をPの極線（polar line）と言う。

反転幾何学

→詳細は「反転幾何学」を参照

特に円の場合、調和共役は円による反転と等しい。これはSmogorzhevskyの定理の一つである^[27]。

円k, q が垂直に交わっているときk,qの中心を結ぶ直線とqの2つの交点はkについて、反転の関係にある。また、kの中心,kと直線のq側の交点に対してk,qの中心を結ぶ直線とqの2つ交点は調和共役の関係にある。

円錐曲線とJoachimthalの等式

${\displaystyle C}$を以下の式で表される楕円とする。

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}$

楕円の外にある点 ${\displaystyle P(x_{0},y_{0})}$ について、${\displaystyle P}$を通る直線${\displaystyle L}$が楕円と${\displaystyle A}$,${\displaystyle B}$で交わっている。 ${\displaystyle A}$ の座標を ${\displaystyle (\xi ,\eta )}$とする。${\displaystyle L}$上の点${\displaystyle Q(x,y)}$を、${\displaystyle A}$が${\displaystyle PQ}$を${\displaystyle 1}$:${\displaystyle \lambda }$に内分する、楕円の内部に位置する点とすると、以下が成り立つ。

${\displaystyle PA={\sqrt {(x_{0}-\xi )^{2}+(y_{0}-\eta )^{2}}}=1,\;\;\;AQ={\sqrt {(x-\xi )^{2}+(y-\eta )^{2}}}=\lambda }$.

これらの方程式を𝜉と𝜂について解く代わりに、以下の式が解であることを代入によって調べることができる。

${\displaystyle (\xi ,\eta )={\bigg (}{\frac {\lambda x+x_{0}}{\lambda +1}},{\frac {\lambda y+y_{0}}{\lambda +1}}{\bigg )}.}$

${\displaystyle A}$が${\displaystyle C}$上にあることは以下の式から確かめられる。

${\displaystyle {\frac {1}{a^{2}}}{\bigg (}{\frac {\lambda x+x_{0}}{\lambda +1}}{\bigg )}^{2}+{\frac {1}{b^{2}}}{\bigg (}{\frac {\lambda y+y_{0}}{\lambda +1}}{\bigg )}^{2}=1,}$

${\displaystyle \lambda ^{2}{\bigg (}{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-1{\bigg )}+2\lambda {\bigg (}{\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}-1{\bigg )}+{\bigg (}{\frac {x_{0}^{2}}{a^{2}}}+{\frac {y_{0}^{2}}{b^{2}}}-1{\bigg )}=0.}$

この等式は${\displaystyle \lambda }$のJoachimthal's equationと呼ばれる。Joachimthal's equationの2つの根${\displaystyle \lambda _{1},\lambda _{2}}$は${\displaystyle P}$,${\displaystyle Q}$に対する${\displaystyle A}$,${\displaystyle B}$の位置を決定する。

${\displaystyle QA={\frac {1}{\lambda _{1}+1}}(x-x_{0},y-y_{0}),\;\;PA={\frac {\lambda _{1}}{\lambda _{1}+1}}(x_{0}-x,y_{0}-y)}$${\displaystyle QB={\frac {1}{\lambda _{2}+1}}(x-x_{0},y-y_{0}),\;\;PB={\frac {\lambda _{2}}{\lambda _{2}+1}}(x_{0}-x,y_{0}-y).}$

${\displaystyle {\frac {PB}{PA}}{\frac {QA}{QB}}={\frac {\lambda _{2}}{\lambda _{1}}}.}$

上の等式の両辺が${\displaystyle -1}$と等しいならば

${\displaystyle {\frac {QA}{PA}}=-{\frac {QB}{PB}}.}$

このとき ${\displaystyle PQ}$に対する${\displaystyle A}$ の内分比と${\displaystyle B}$の外分比は等しい。すなわちこれは調和比である。

${\displaystyle {\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}-1=0.}$

この等式は ${\displaystyle P(x_{0},y_{0})}$を極とする極線を表す。