四角形
4つの辺と頂点を持つ多角形 ウィキペディアから
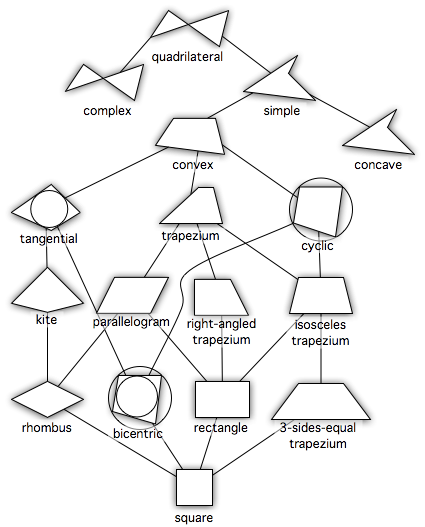
四角形(しかくけい、しかっけい、英: quadrilateral、tetragon)は、平面上で4本の直線に囲まれた平面の一部を指す。多角形の一種で、4つの頂点と4本の辺を持つ。一般的には凸四角形を指す。
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
四角形に関する用語
四角形の分類
- 台形(英: trapezoid、trapezium): 少なくとも一組の対辺が平行であるような四角形。平行な対辺の組を底辺と呼び、残りの対辺の組を脚と呼ぶ。
- 等脚台形(英: isosceles trapezium): 台形のうち、1つの底辺をはさむ 2角の大きさが等しいもの。
- 底辺の中点を結ぶ直線が線対称の軸となり、2本の脚の長さが等しくなる。
- 2本の対角線は、長さが等しい。円に内接する。
- 凧形(英: kite):それぞれ長さの等しい2辺によってはさまれた対角を持つ四角形。
- 対角線の1つが線対称の軸となり、残り一組の対角は等しい大きさを持つ。
- 2本の対角線は、互いに直交する。
- 円に外接する。
- 長方形(矩形、英: rectangle): 4角の大きさが全て等しい四角形。
- 菱形(斜方形、英: rhombus): 4辺の長さが全て等しい四角形。
- 1辺の長さは、周の4分の1に等しい。
- 4辺は、対角線の交点から等距離にある(円に外接する)。
- 平行四辺形の特別な形であるので、平行四辺形の性質を全て持つ。
- 凧形の特別な形であるので、凧形の性質を全て持つ。
- 正方形(スクエア、英: square): 4辺の長さが全て等しく、4角の大きさが全て等しい四角形。
- 対角線の長さは等しく、直角に交わる。
- 正多角形の一種であり、正多角形の性質を全て持つ。
- 長方形の特別な形であるので、長方形の性質を全て持つ。
- 菱形の特別な形であるので、菱形の性質を全て持つ。
- 平行四辺形(英: parallelogram): 2組の対辺がそれぞれ平行である四角形。
- 対辺は(2組あるが、それぞれ)長さが等しくなっている。
- 対角は(2組あるが、それぞれ)大きさが等しくなっている。
- 対角線は(2本あるが、そのどちらも)他の対角線の中点を通る。対角線は、互いの長さを2 等分する。
- 凹四角形: 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。
- 円に外接する四角形:内接円を持つ四角形。2組の対辺の和が等しい。
- 円に内接する四角形:外接円を持つ四角形。2組の対角の和はそれぞれ 180°(π ラジアン)に等しい。4つの内角の大きさが、その対角の外角に等しい。
- 双心四角形:内接円と外接円を持つ四角形。
合同条件
二つの四角形を、それぞれその対角線の一つで分割したとき、分割された図形は三角形になる。この三角形が合同である組が存在して、対角線となる辺の位置も一致しているとき、二つの四角形は合同になる。
相似条件
この節の加筆が望まれています。 |
面積の公式
| 正方形 | [一辺]2 |
| 長方形 | [縦]×[横] |
| 菱形・凧形・直交対角線四角形 | [対角線]×[もう一つの対角線]÷2 |
| 平行四辺形 | [底辺]×[高さ] |
| 台形 | ([上底]+[下底])×[高さ]÷2 |
| 円に内接する四角形(共円四辺形) | ブラーマグプタの公式 |
| 円に外接する四角形 | [ 内接円の半径]×[ 周の長さの半分 ] |
| 一般の四角形 | ブレートシュナイダーの公式 [対角線]×[もう一つの対角線]×[sin([2つの対角線がなす角])]÷2 |
関連項目
Wikiwand - on
Seamless Wikipedia browsing. On steroids.

